25 CÂU HỎI
Một cửa hàng bán 2 loại áo phông A và B. Nếu bán mỗi chiếc áo loại A giá X đôla và mỗi chiếc áo loại B giá Y đôla thì mỗi ngày người tiêu dùng sẽ mua 22-3x+2y chiếc áo loại A và 22+2x-5y chiếc áo loại B. Để thu được doanh thu tối đa người chủ cửa hàng nên định giá bán mỗi loại bao nhiêu
A. 15 và 17
B. 7 và 5
C. 5 và 7
D. 17 và 15
Sử dụng tính xấp xỉ bằng số gia ta tính đc lượng thay đổi giá trị của hàm số f(x)= 6x2+9x+5 khi x giảm từ 4 xuống 3.9 xấp xỉ bằng
A. -5.7 đơn vị
B. 2.7 đơn vị
C. 5.7 đơn vị
D. -2.7 đơn vị
Cho hàm số y= 3x2-2x+1. Độ dốc của tiếp tuyến với đồ thị tại điểm có hoành độ x=2 là
A. 10
B. 5
C. 9
D. 2
Tốc độ thay đổi sản lượng của 1 nhà máy là Q’(t)=4t3-3t2 +10t+3 đơn vị mỗi giờ, với t là số giờ sau khi bắt đầu ca sáng lúc 8h. Số đơn vị được sản xuấttừ 8h sáng đến 12h trưa là
A. 66
B. 165
C. 224
D. 284
Cho hàm số g(x) thỏa mãn g(-2)=-1 và g’(-2)=-2 hàm số f(x)=[ 3x3-4g(x)]7g(x)+1 Khi đó f’(-2) =
A. 16
B. 71
C. 18
D. -40
Chi phí cận biên một loại sản phẩm là 6q2-8q+200 đôla mỗi đơn vị khi q đơn vị được sản xuất. Chi phí để Sản xuất 3 đơn vị đầu tiên là 718 đôla. Chi phí để sản xuất 5 đơn vị đầu tiên là
A. $1250
B. $2510
C. $1520
D. $2150
Cho hàm số f(x), g(x) liên tục trên [-1;4] và thỏa mãn: ![Cho hàm số f(x), g(x) liên tục trên [-1;4] và thỏa mãn: , , . Khi đó (ảnh 1)](https://video.vietjack.com/upload2/images/1744513162/1744513167-image4.png)
![Cho hàm số f(x), g(x) liên tục trên [-1;4] và thỏa mãn: , , . Khi đó (ảnh 2)](https://video.vietjack.com/upload2/images/1744513162/1744513167-image5.png) ,
, ![Cho hàm số f(x), g(x) liên tục trên [-1;4] và thỏa mãn: , , . Khi đó (ảnh 3)](https://video.vietjack.com/upload2/images/1744513162/1744513167-image10.png) ,
, ![Cho hàm số f(x), g(x) liên tục trên [-1;4] và thỏa mãn: , , . Khi đó (ảnh 4)](https://video.vietjack.com/upload2/images/1744513162/1744513167-image7.png) . Khi đó
. Khi đó ![Cho hàm số f(x), g(x) liên tục trên [-1;4] và thỏa mãn: , , . Khi đó (ảnh 5)](https://video.vietjack.com/upload2/images/1744513162/1744513167-image9.png)
A. 7
B. 1
C. -13
D. 5
Kết luận đúng về tích phân suy rộng 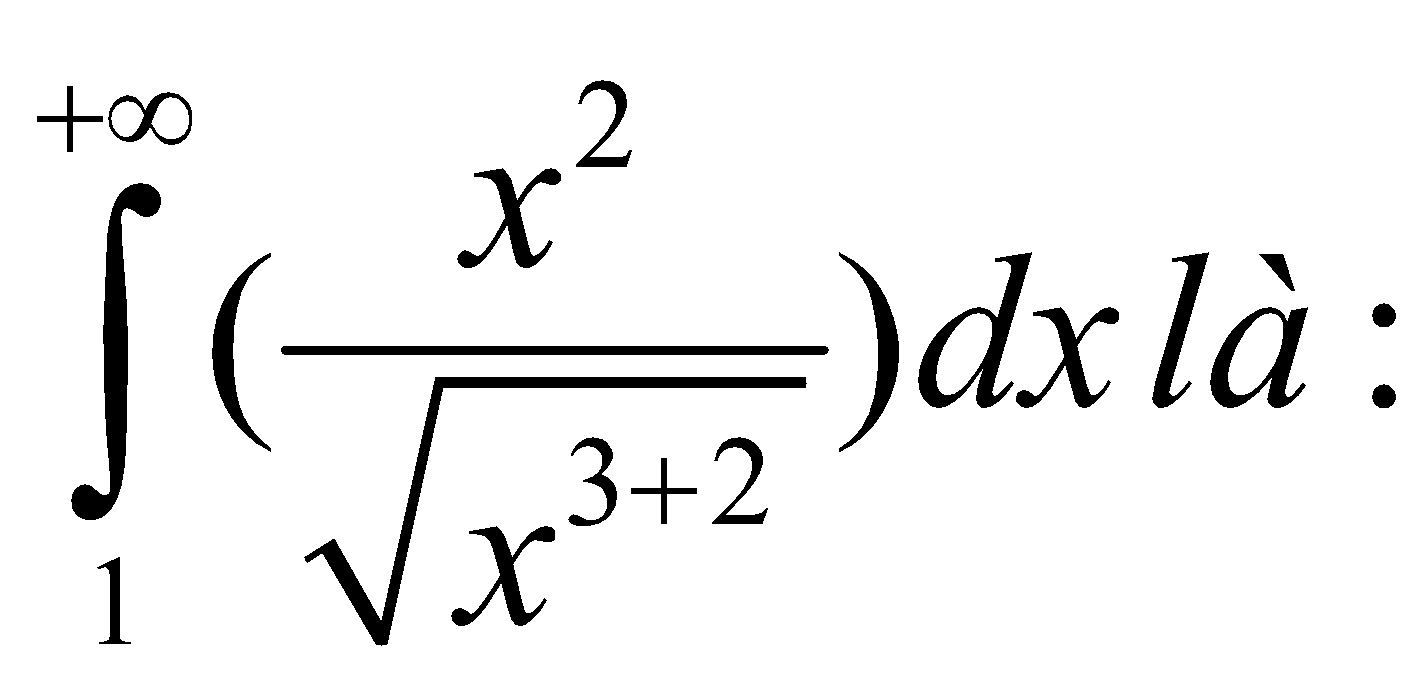
A. Tích phân hội tụ và bằng![]()
B. Tích phân hội tụ và bằng![]()
C. Tích phân phân kỳ
D. Tích phân hội tụ và bằng 0
Một người đang làm 1 chiếc hộp trưng bày ở bảo tàng được trang trí công phu từ vật liệu có giá 2 mỗi inch vuông cho phần đáy, 4 mỗi inch vuông cho các mặt bên và $8 mỗi inch cho nắp hộp, Nếu thể tích là 90 inches khối thì chọn kích thước của chiếc hộp để tối thiểu hóa tổng chi phí làm hộp bằng cách giải bài toán
A. Tìm cực tiểu của hàm C= 2yz+4(2xy+2xz) +8yz với điều kiện x+y+z=90
B. Tìm cực tiểu của hàm C= 2yz+4(2xy+2xz) +8yz với điều kiện xyz+90
C. Tìm cực đại của hàm C= 2yz+4(2xy+2xz) +8yz với điều kiện xyz=90
D. Tìm cực tiểu của hàm C= 2yz+4(xy+2xz) +8yz với điều kiện x+y+z=90
Cho biết mức carbon monoxide trung bình hàng ngày trong không khí sẽ là c(p)=0.4p+5 ppm khi dân số của khu vực đó là p nghìn người. Người ta ước tính rằng dân số của khu vực đó t năm sau kể từ bây giờ sẽ là p(t)=0.2t2+4 nghìn người. Khi nào ước tính carbon monoxide trung bình đạt 9 ppm
A. Sau xấp xỉ 2.9 năm sau
B. Sau xấp xỉ 4.2 năm sau
C. Sau xấp xỉ 3.7 năm sau
D. Sau xấp xỉ 5.5 năm sau
Giả sử hàm số f(x;y)= ax2 + 4xy+y2+4x có điểm tới hạn là (x0;y0). Khi đó điểm (x0;y0) là
A. Điểm cực tiểu nếu a<4
B. Điểm cực đại nếu a<4
C. Điểm cực tiểu nếu a>4
D. Điểm cực đại nếu a>4
Giả sử t năm sau một dự án sinh lời với tốc độ P1’(t)=60+t2 trăm đôla mỗi năm. Trong khi đó dự án đàu tư thứ 2 sẽ sinh lời với tốc độ P2’(t) = 180+2t trăm đôla mỗi năm. Biết rằng sau 12 năm kể từ bây giờ tốc độ sinh lời của dự án thứ 1 sẽ vượt thứ 2. Lợi nhuận vượt trội ròng trong khoảng thời gian 12 năm được tính bởi
A. 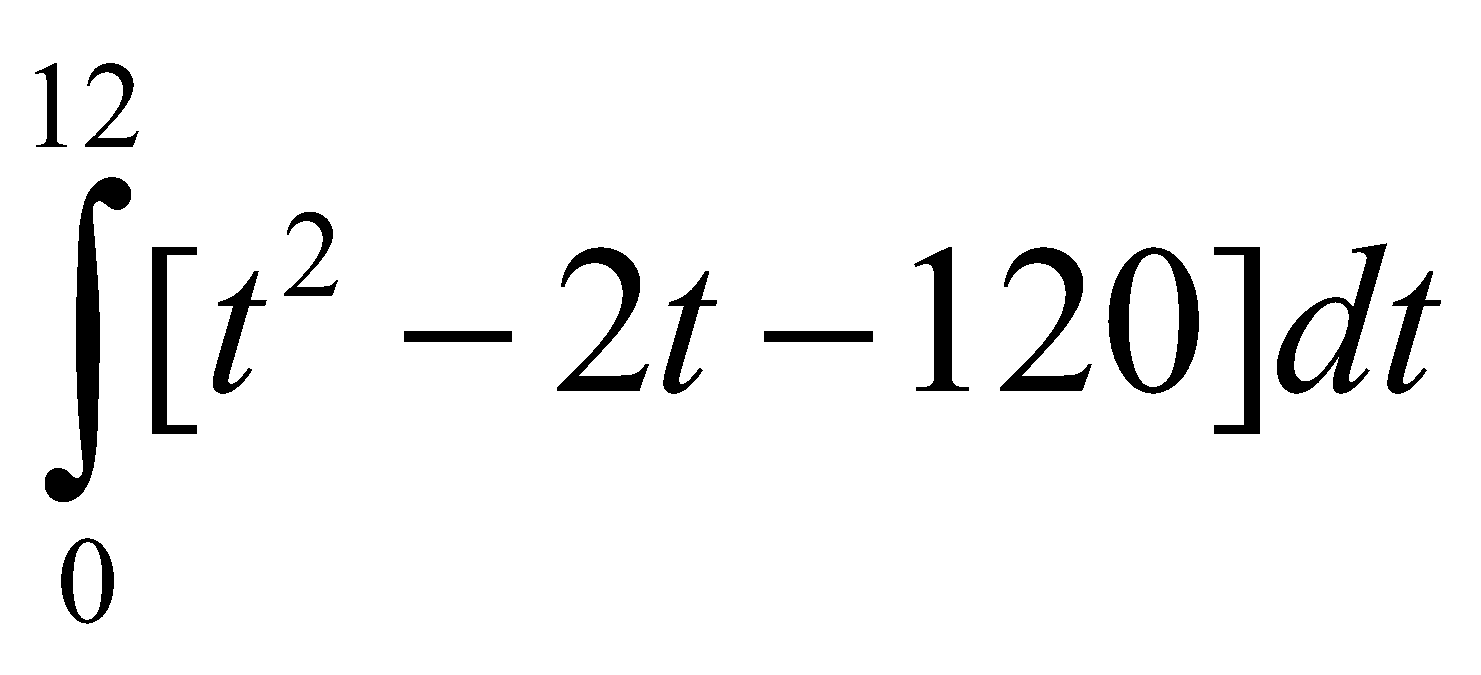
B.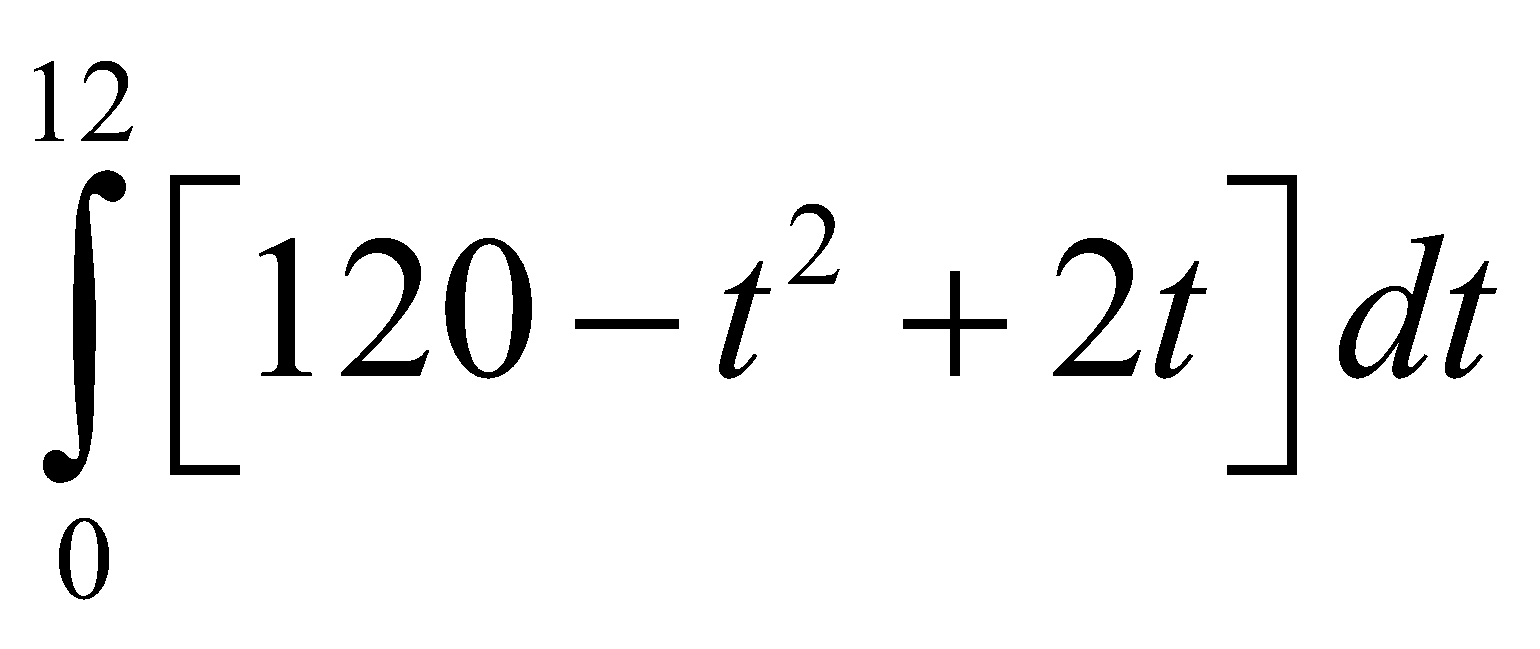
C.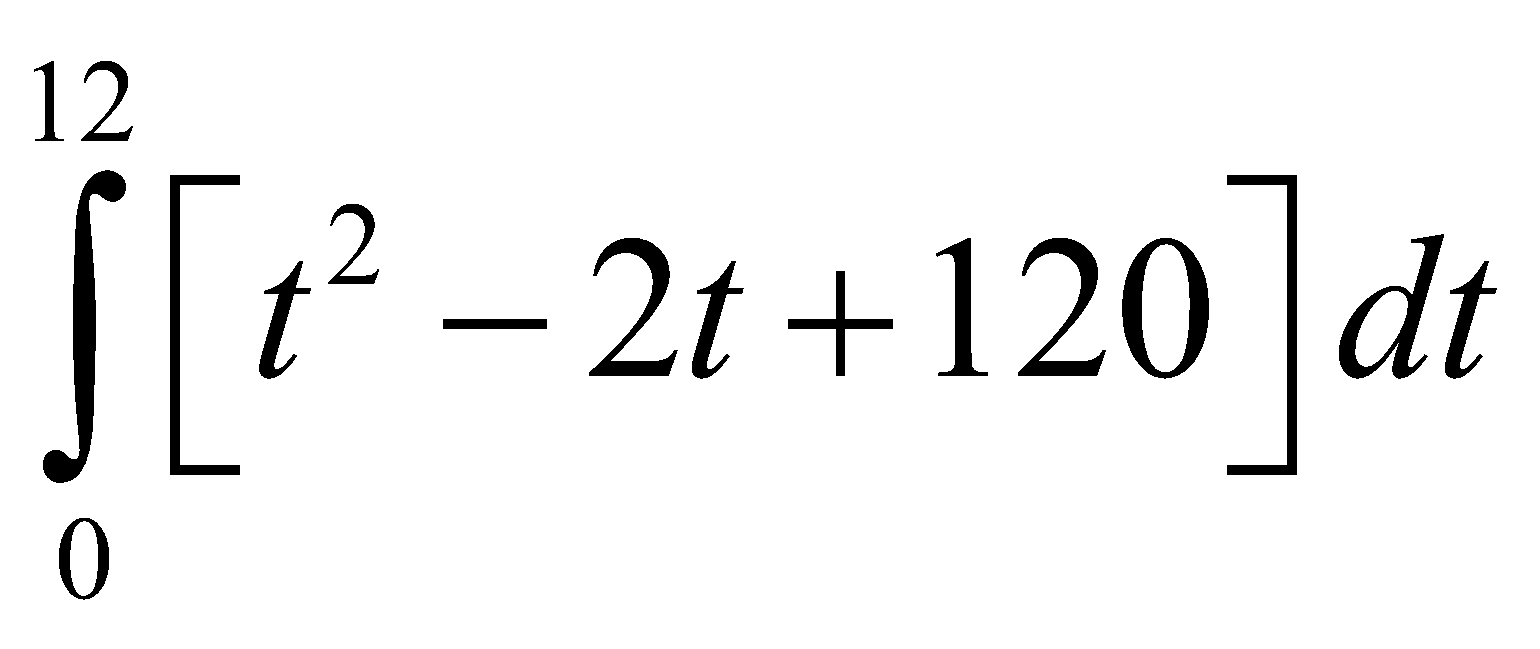
D.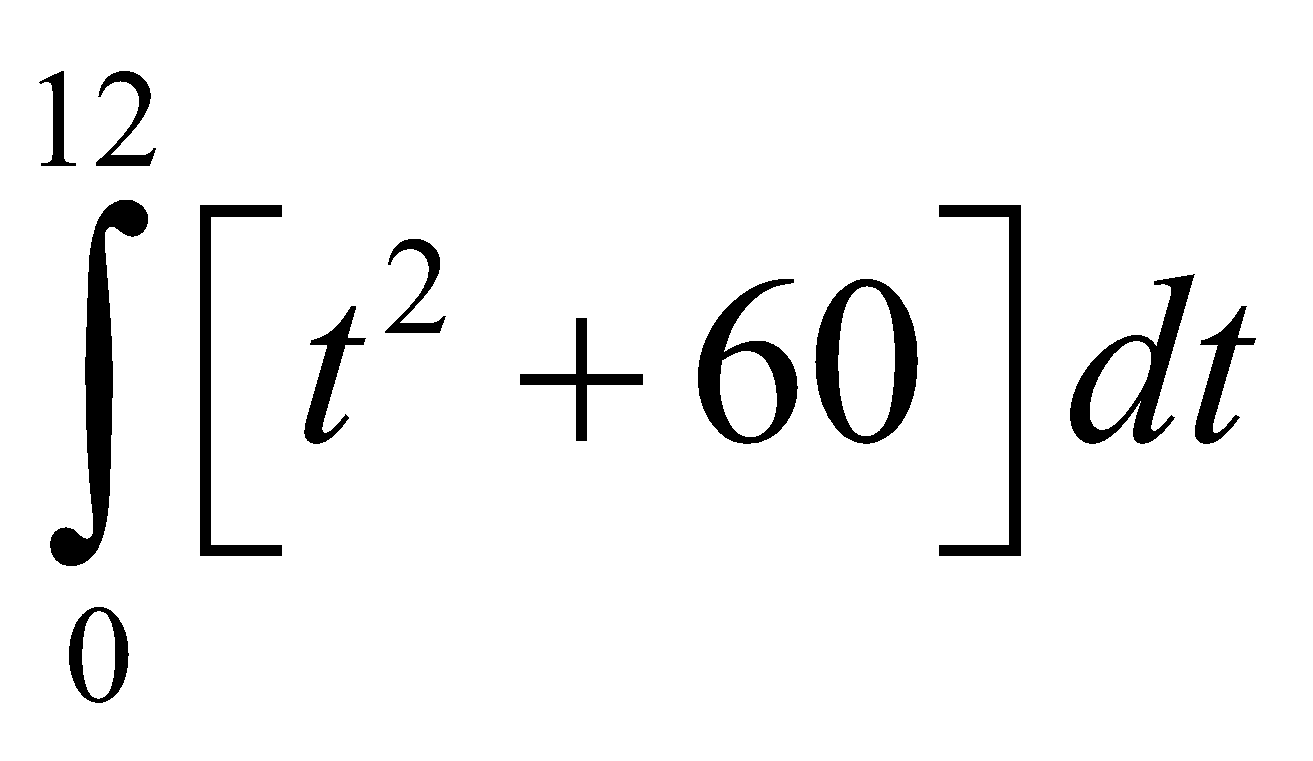
Độ co dãn của cầu theo giá đối với 1 loại hàng hóa tại mức p=p0 là E(p0) =0.38. Kết luận nào sau đây đúng
A. Tại mức giá p0’ nếu tăng 1% thì lượng cầu giảm 0.38%
B. Tại mức giá p0’, nếu tăng 1 đơn vị thì lượng cầu giảm 0.38 đơn vị
C. Tại mức giá p0’, nếu tăng 1 đơn vị thì lượng cầu giảm 0.38%
D. Tại mức giá p0’, nếu tăng 1% thì lượng cầu giảm 0.38 đơn vị
Sau khi ghép cây x năm, một loại cây tăng trưởng với tốc độ h’(x)=0.5 + 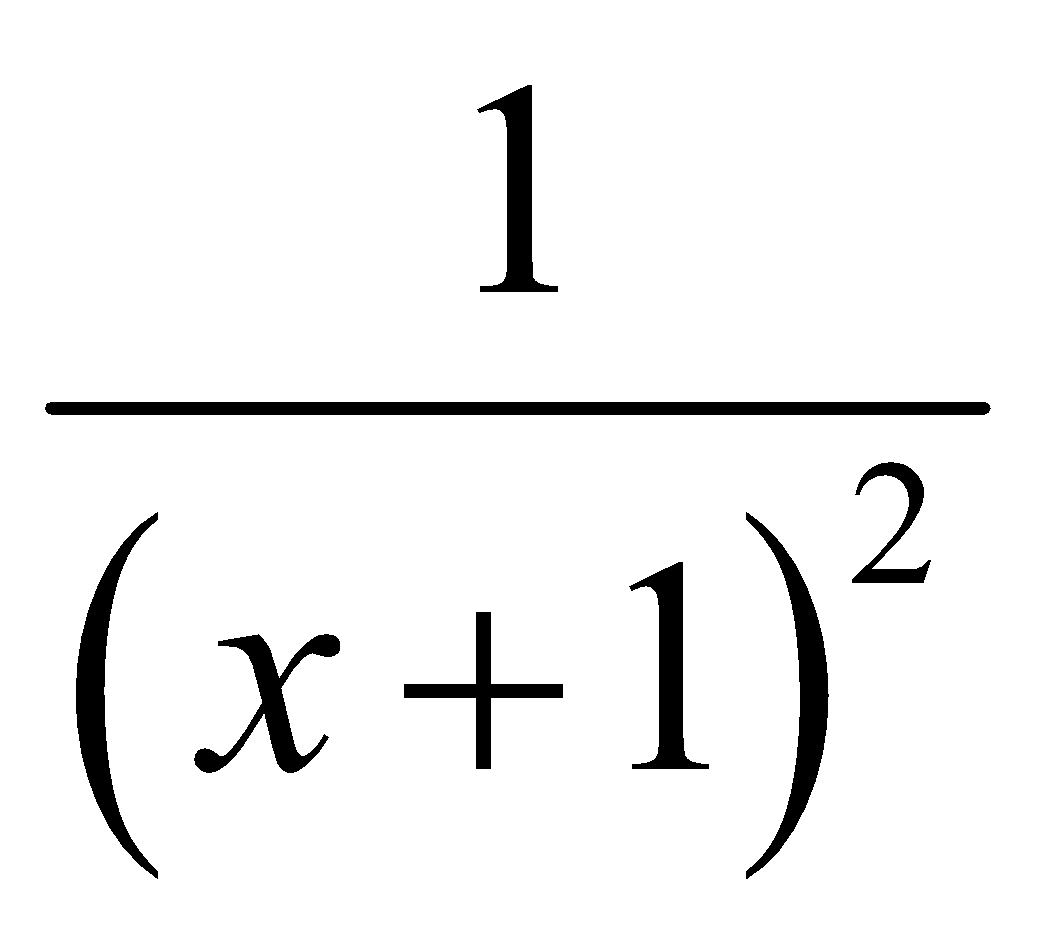 mét mỗi năm. Cây tăng trưởng bao nhiêu mét trong năm thứ 2:
mét mỗi năm. Cây tăng trưởng bao nhiêu mét trong năm thứ 2:
A.![]()
B.![]()
C.![]()
D.![]()
Một doanh nghiệp Sản xuất 1 loại sp có hàm Sản xuất Q = 50K 0.6L 0.4. doanh nghiệp này nhận được hợp đồng cung cấp 900 sản phẩm. Tìm K,L để doanh nghiệp Sản xuất theo hợp đồng tốn ít chi phí nhất khi giá thuê tư bản và lao động lần lượt là 18 và 12. Khi giải bài toán bằng phương pháp nhân tử Lagrange ta lập hàm Lagrange là
A. L = 50K0.6 L0.4 + (900 – 18K – 12L)
B. L = 18K+12L + (900 - 50K0.6 L0.4)
C. L= (18K+12L) + 900 - 50K 0.6 L0.4
D. L= (50K 0.6 L 0.4) + (900 - 18K-12L )
Cho hàm số y=5x2 − 4cosx + 3. Đạo hàm y′ là:
A. y′=10x+4sinx+3
B. y′=10x+4sinx
C. y′=10x−4sinx
D. y′=10x−4sinx+3
Cho hàm số y=(5x2−3x−1)6 . y′(1) có giá trị là:
A. 42
B. 1
C. 6
D. -42
Cho hàm số y = sin(2x−5). Đạo hàm y′ là:
A. y′=cos(2x−5)
B. y′=2.cos(2x−5)
C. y′=sin(2)
D. y′=2.sin(2x−5)
Biểu thức vi phân của hàm y = x2 . e-5x là:
A. dy = −5x2.e−5x.dx
B. dy = 2x.e−5x.dx
C. dy = −10x.e−5x.dx
D. dy = (2x−5x2)e−5x.dx
Cho hàm số y = ln(2x2 - 5x + 8). Tập xác định của hàm số là:
A. (−∞,2]
B. (2,+∞)
C. R
D. [2,+∞)
Đạo hàm của y = ![]() là:
là:
A. y′ = 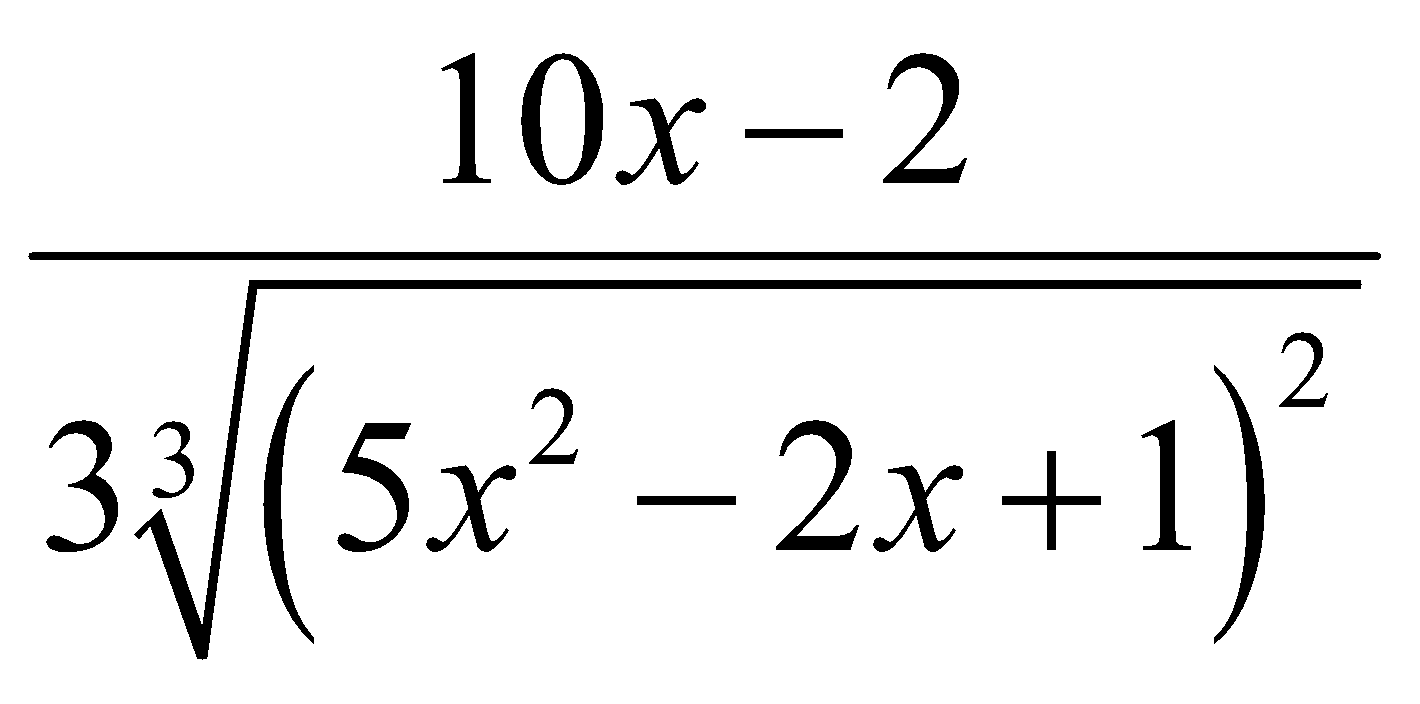
B. y′ =![]()
C. y′ =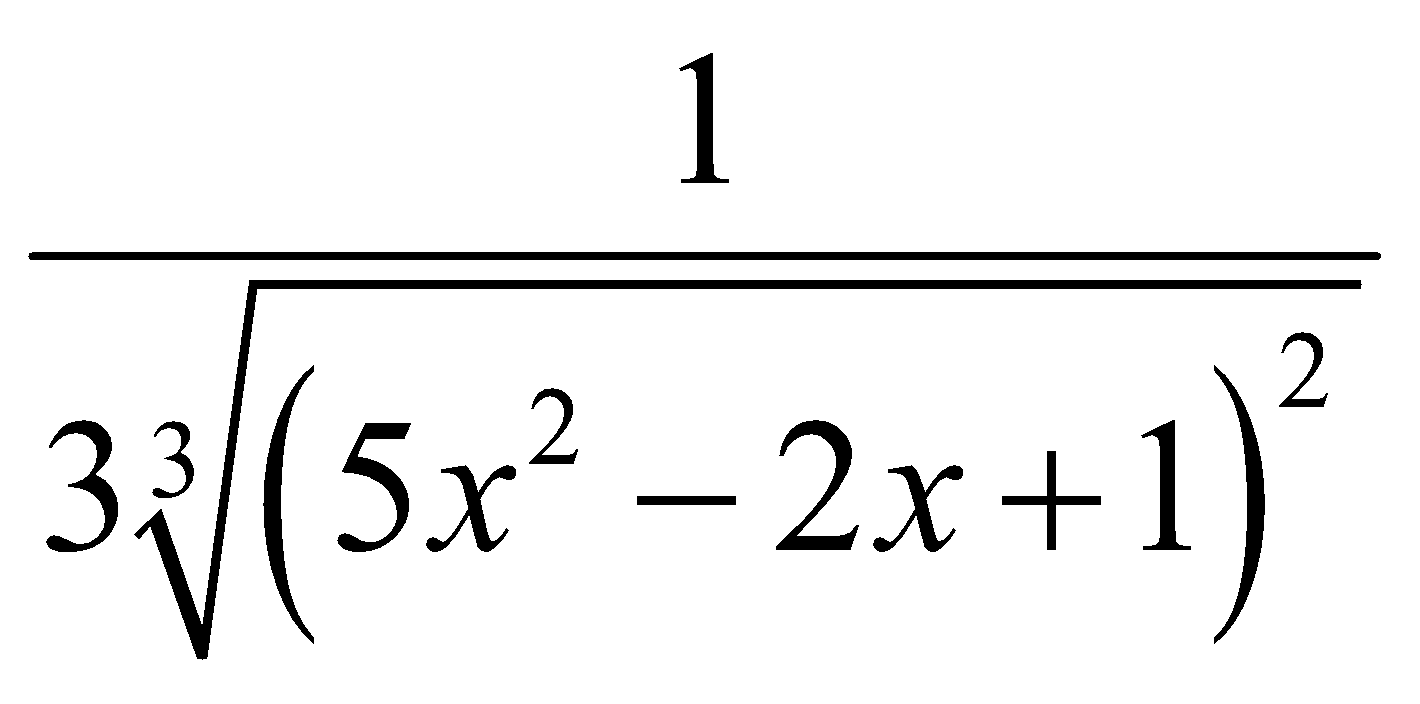
D. y′ = 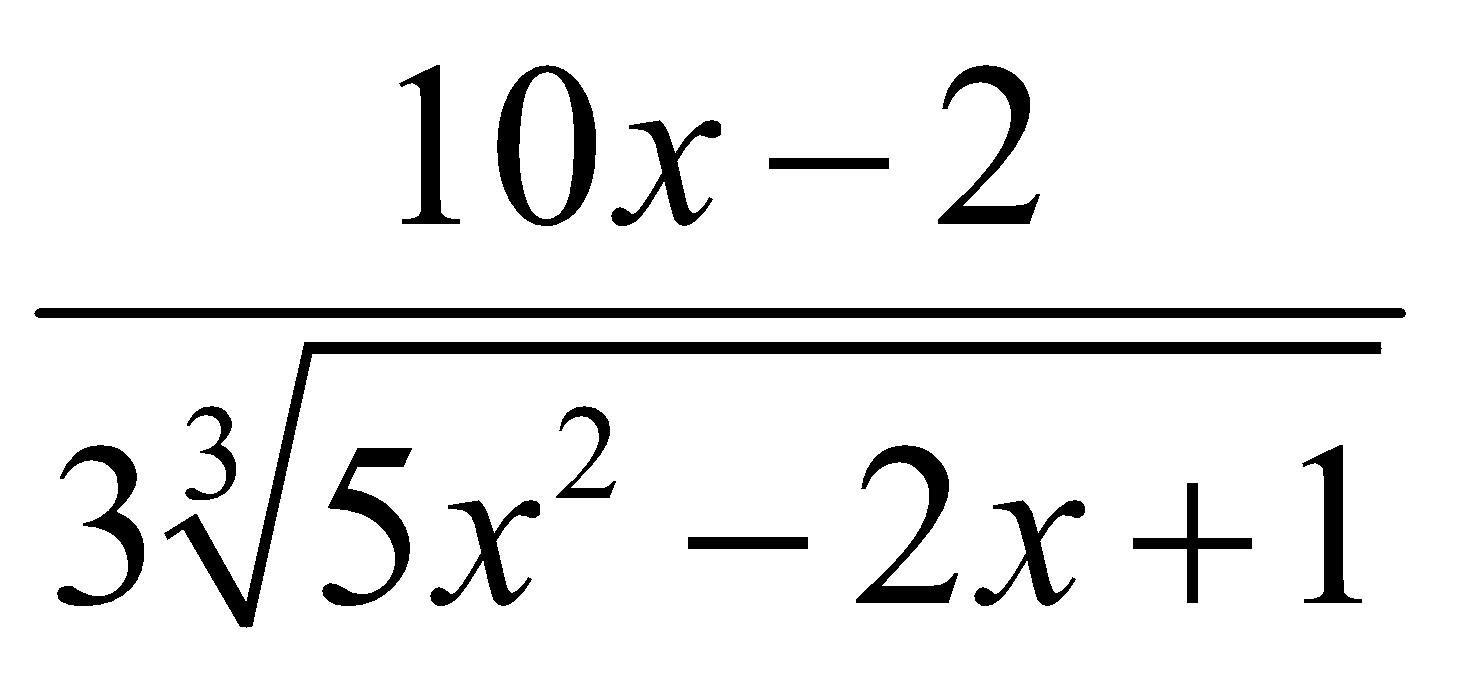
Cho hàm số y = ln3(2x), giá trị y’ (![]() là:
là:
A. y′(![]() ) =
) = ![]()
B. y′(![]() ) = 3
) = 3
C. y′(![]() ) =
) =![]()
D. y′(![]() ) =
) =![]()
Cho hàm số y = ln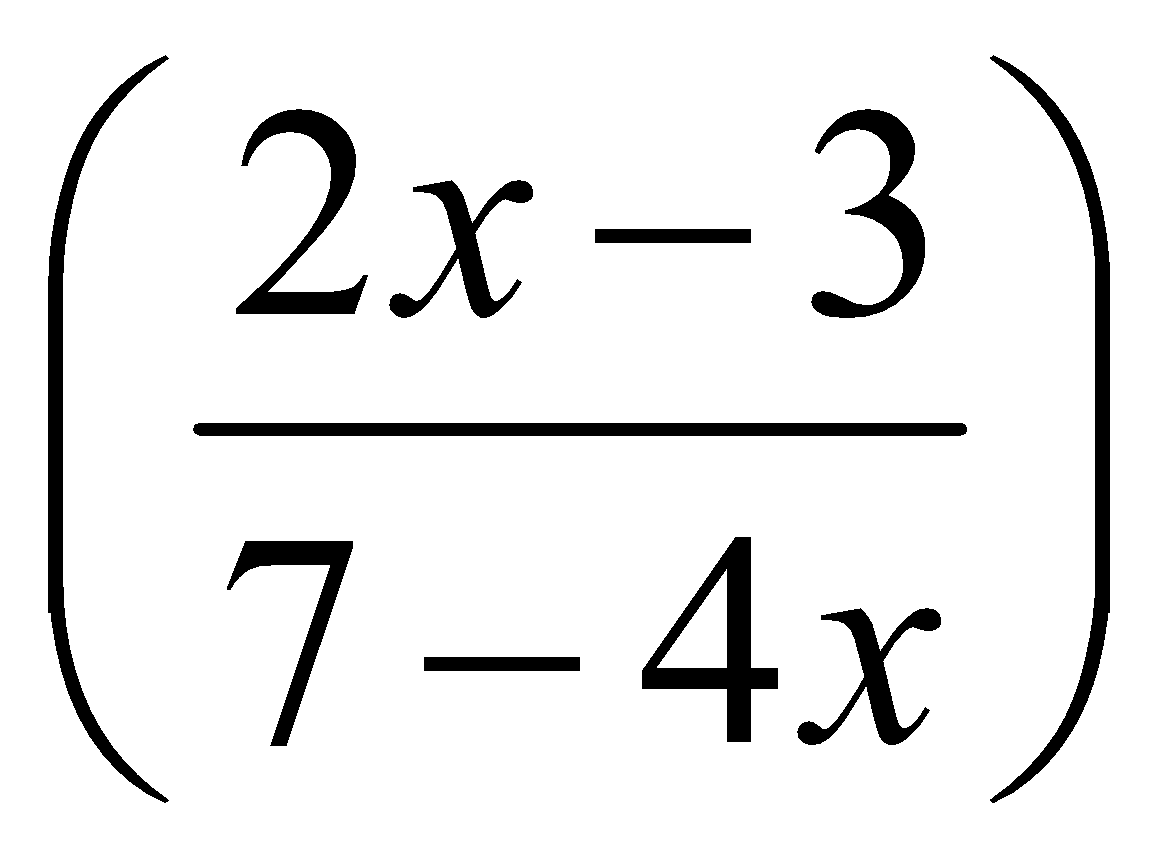 . Đạo hàm y’ có giá trị là:
. Đạo hàm y’ có giá trị là:
A. y’ = 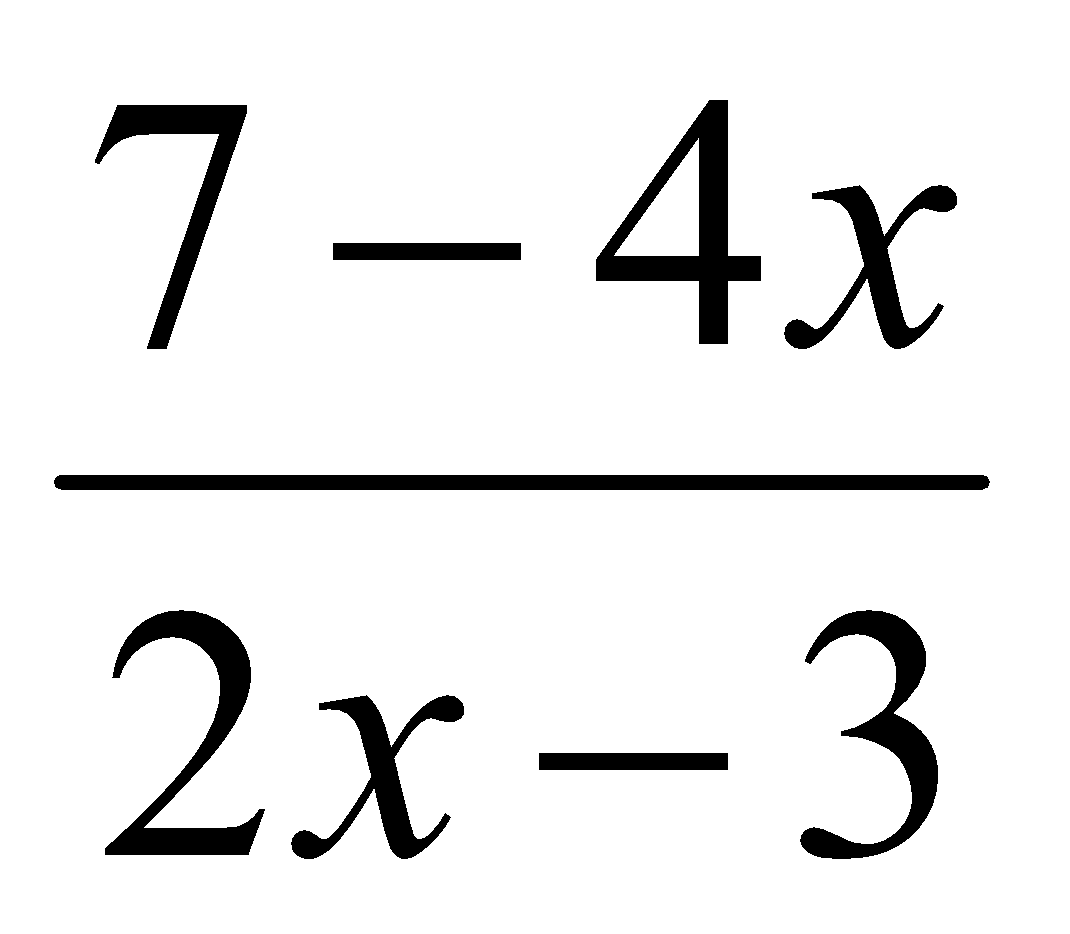
B. y’ =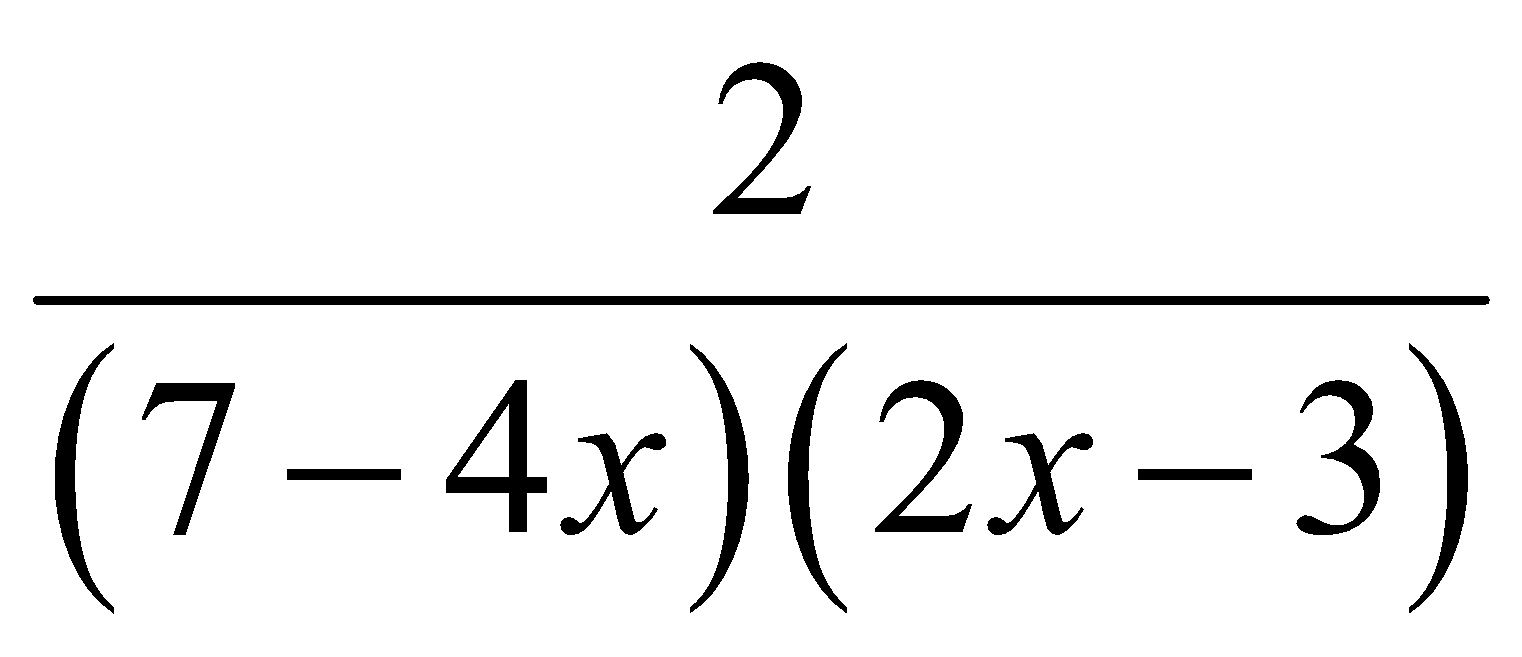
C. y’ =![]()
D. y’ = ln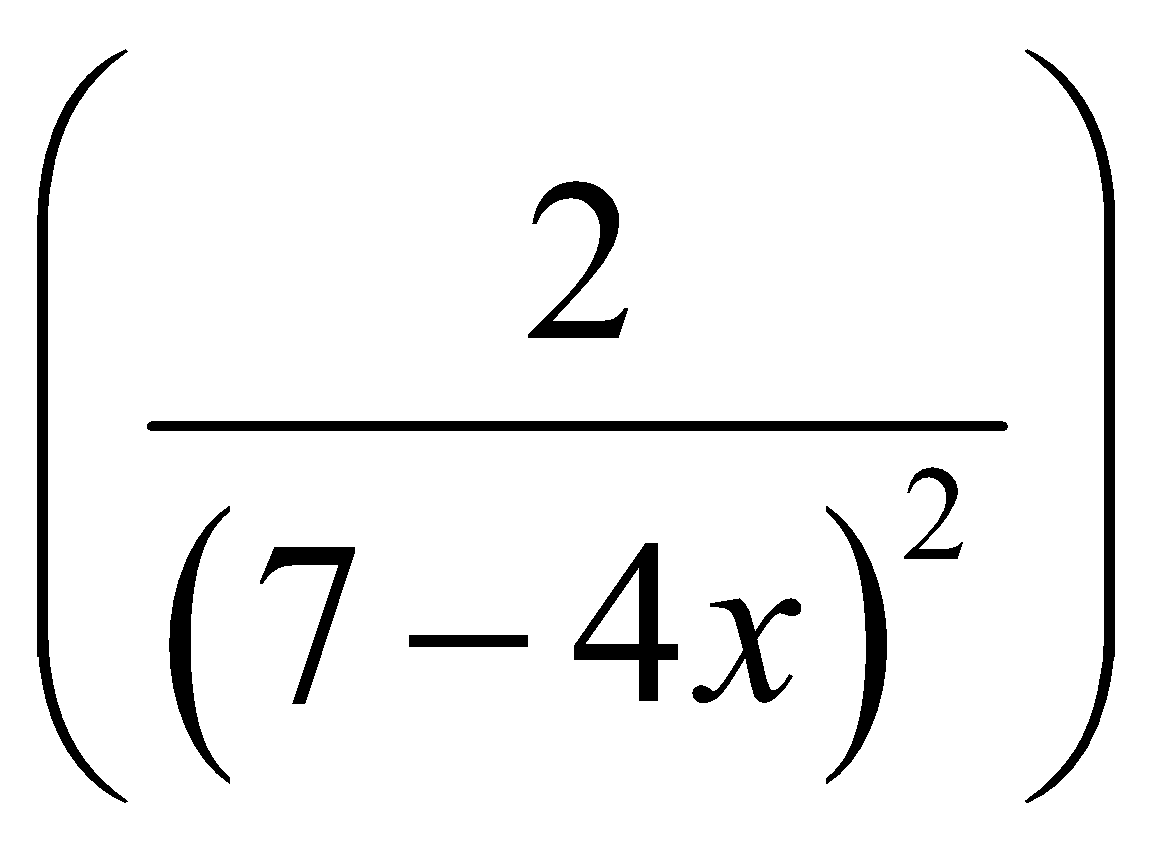
y = sin(![]() . Đạo hàm y’ là:
. Đạo hàm y’ là:
A. y’ = 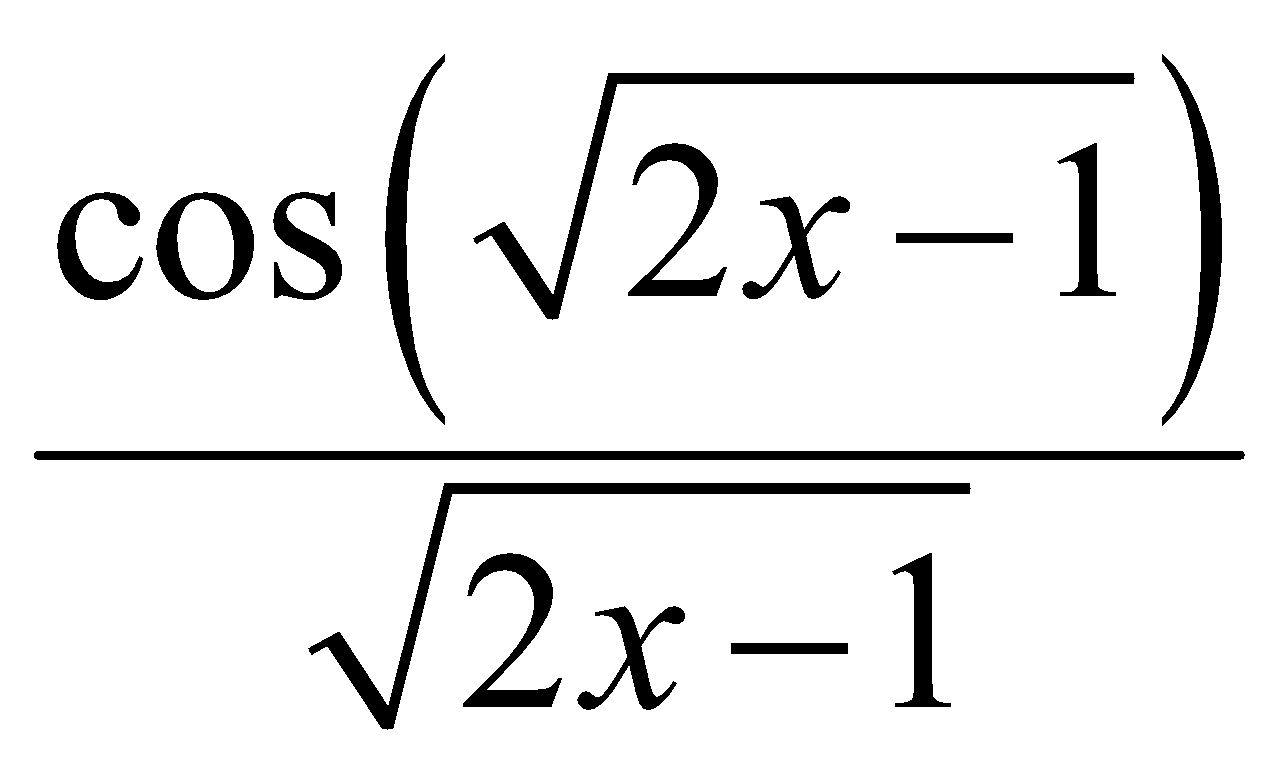
B. y’ = cos(![]()
C. y’ =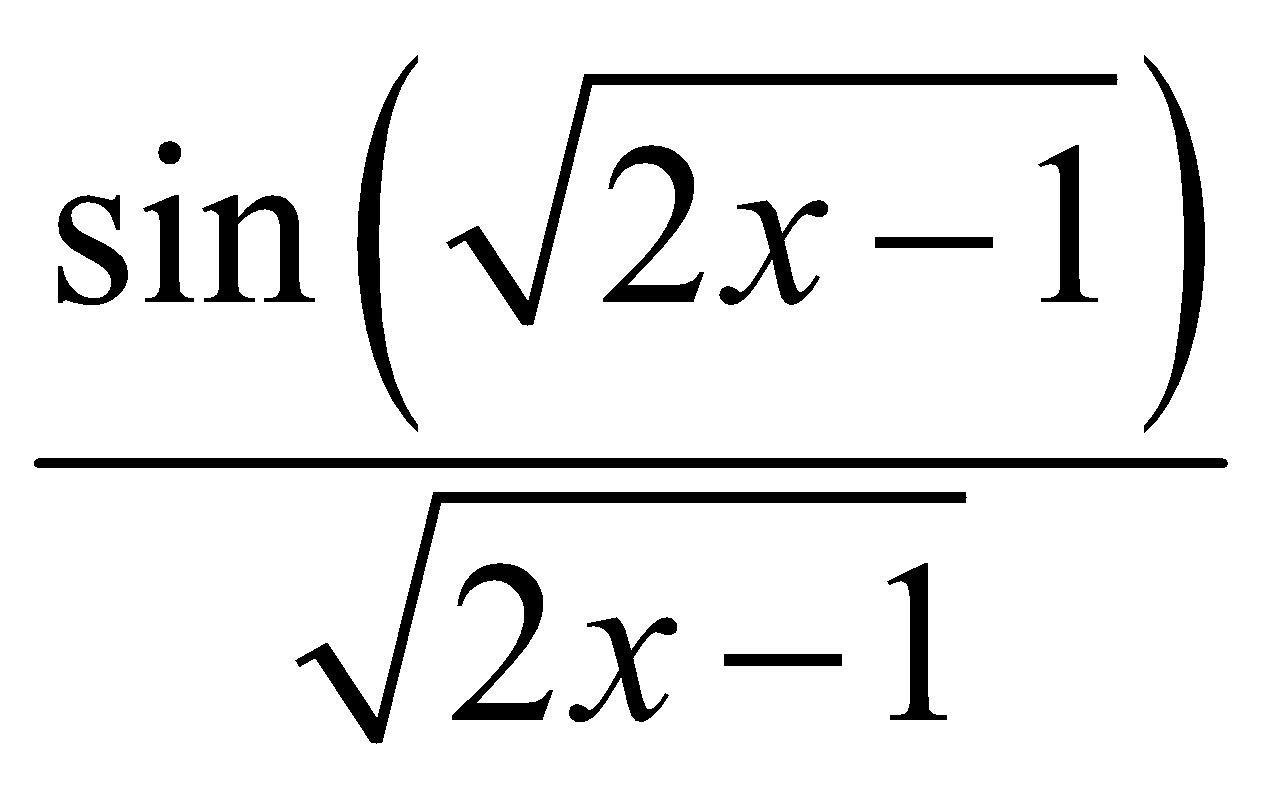
D. y’ = sin(![]() )
)
Cho hàm số y = ![]() . Số điểm cực trị của hàm số là:
. Số điểm cực trị của hàm số là:
A. 1
B. 4
C. 2
D. 3
