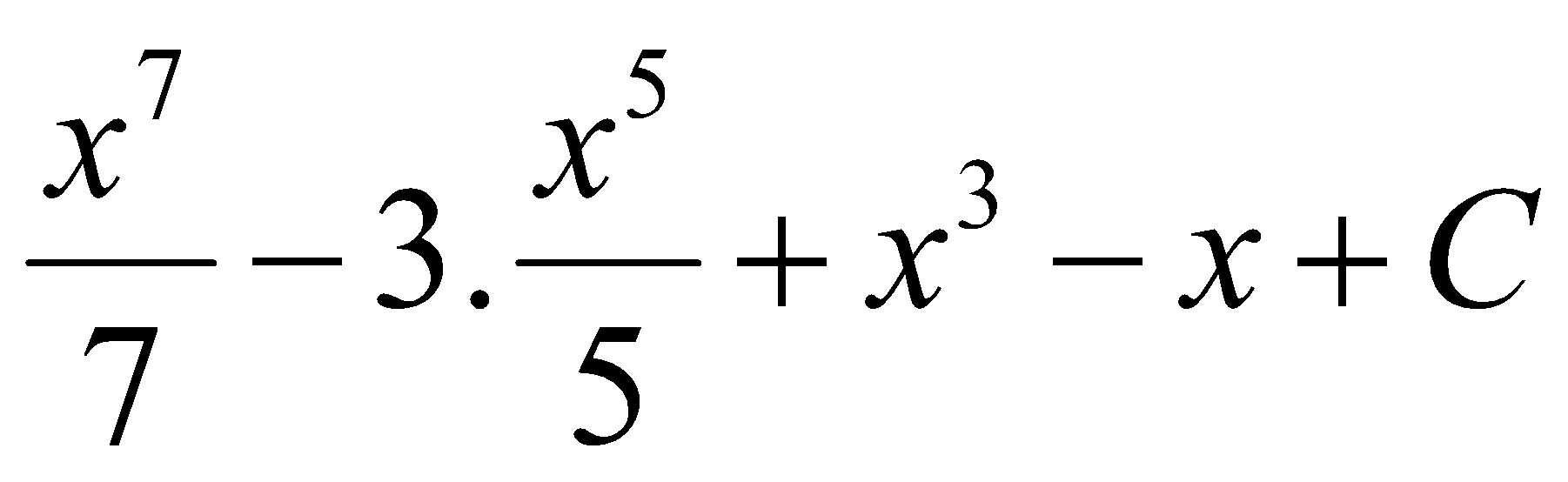26 CÂU HỎI
Cho hàm số y = ![]() .
.![]() +
+ ![]() . Tập xác định của hàm số là:
. Tập xác định của hàm số là:
A. {1,3}
B. (-∞,1∪3,+∞)
C. R
D. [1,3]
Với hàm số y = x . e2x thì df(![]() ) với số gia
) với số gia ![]() = 0,1 có giá trị là:
= 0,1 có giá trị là:
A. 0,2e
B. 0,1e
C. 0,3e
D. 1,5e
Cho hàm số y = ![]() . Đạo hàm cấp 2 y’’ là:
. Đạo hàm cấp 2 y’’ là:
A. y’’ = 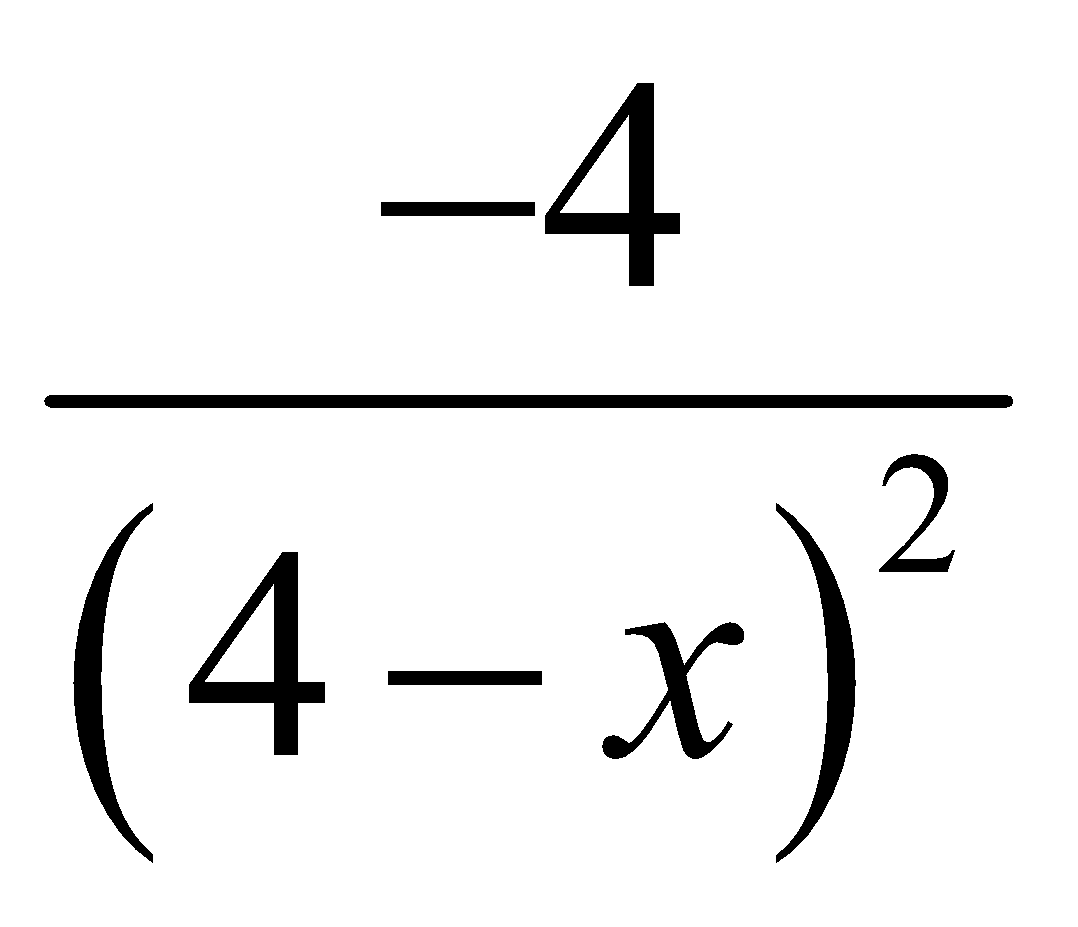
B. y’’ =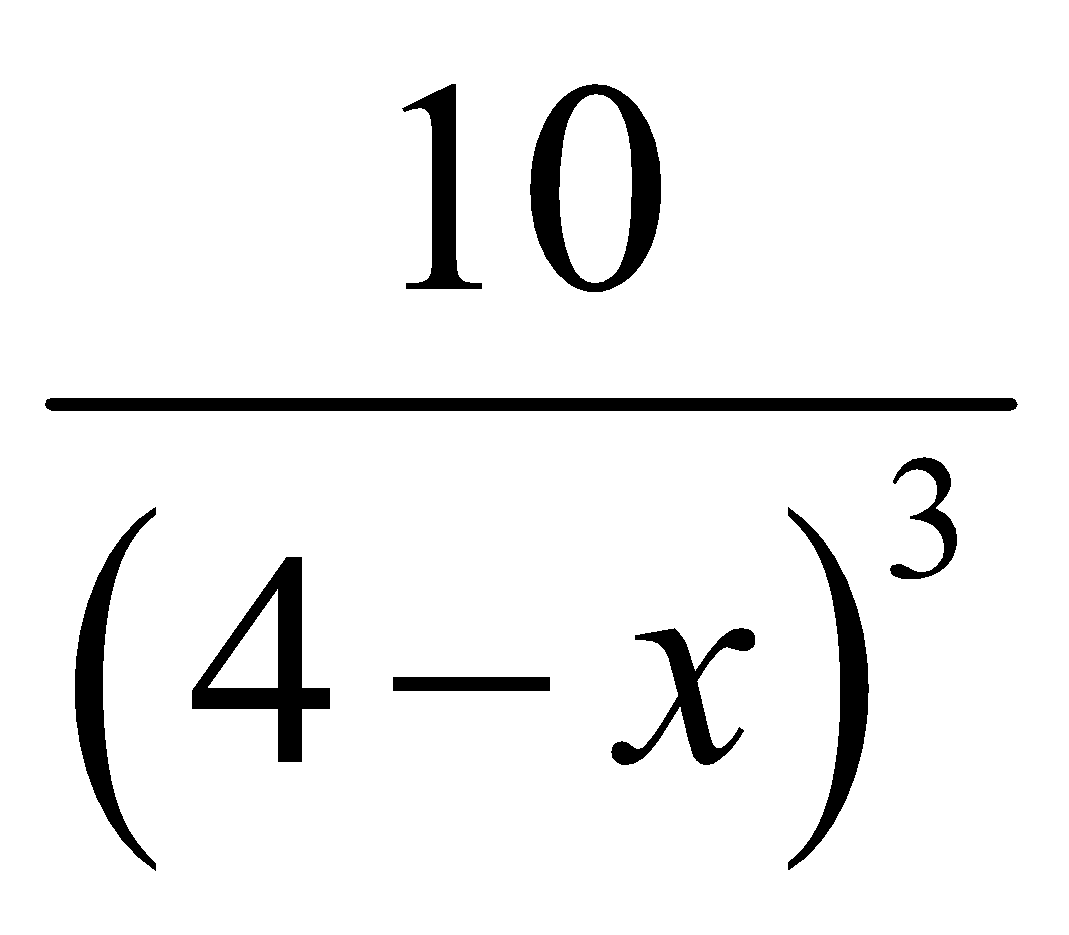
C. y’’ = -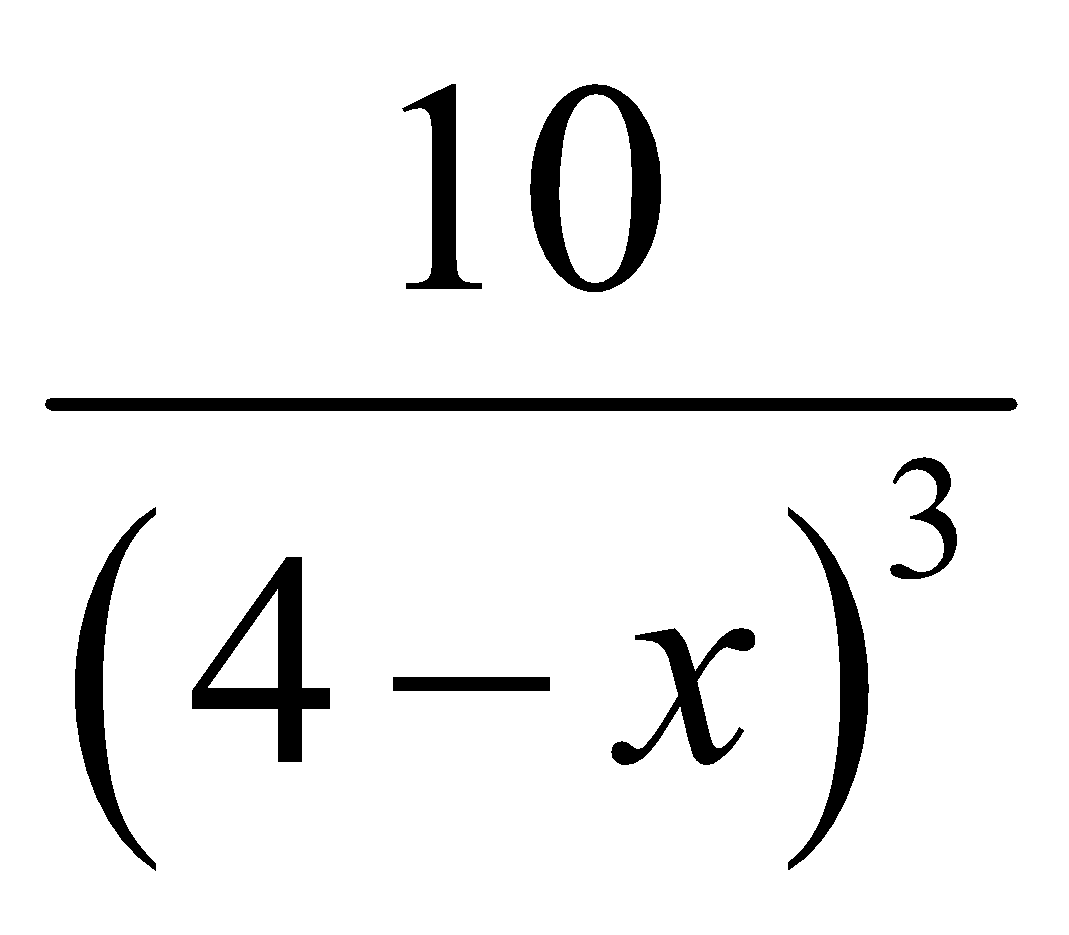
D. y’’ = ![]()
Cho hàm số y = ![]() . Tập xác định của hàm số là:
. Tập xác định của hàm số là:
A. [1,+∞)
B. [13,1]
C. (−∞,13]
D. [13,+∞)
Cho y = (3x – 2) . e-2x. Giá trị của y’’(1) là:
A. y’’(1) = 8e2
B. y’’(1) = -7e 2
C. y’’(1) = -8e-2
D. y’’(1) = -8e2
Đạo hàm của y = (2x-1) . tan (1-4x) là:
A. y′ = 2tan(1−4x) −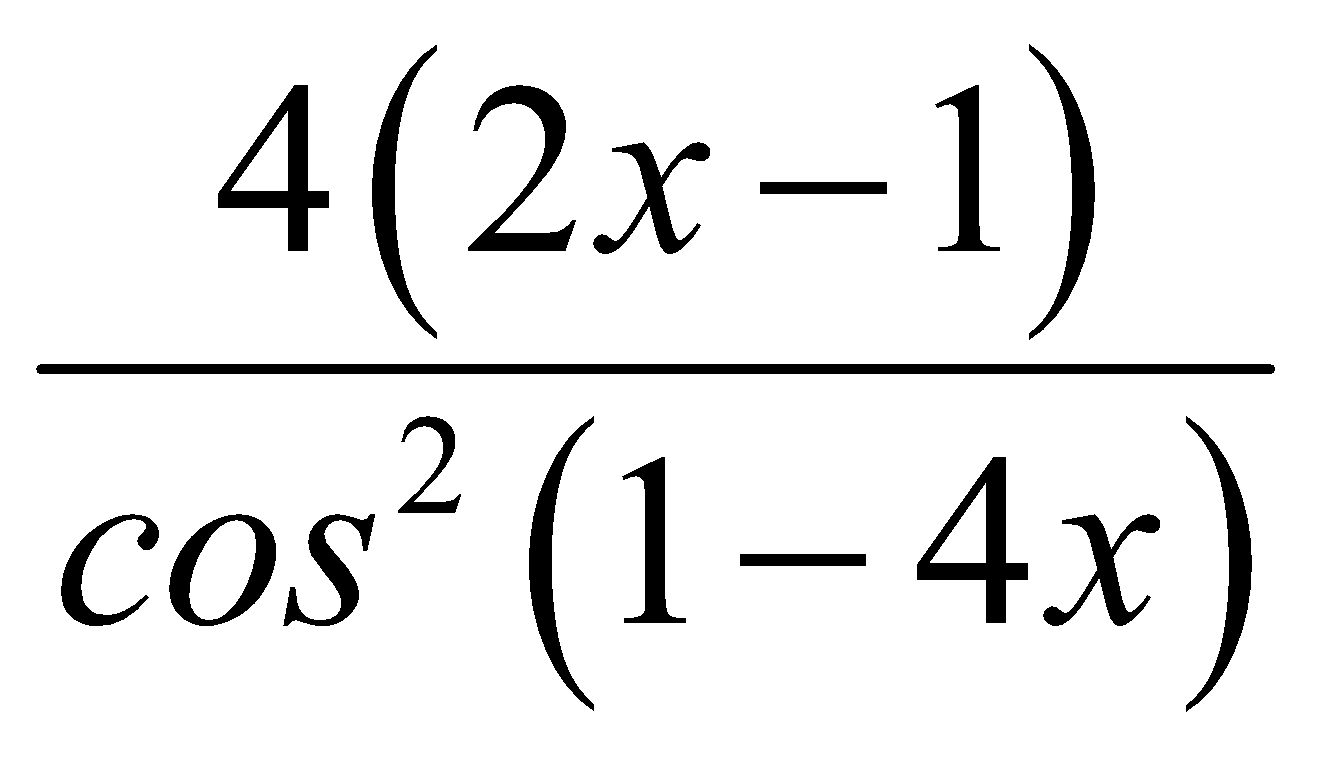
B. y′ = 2x−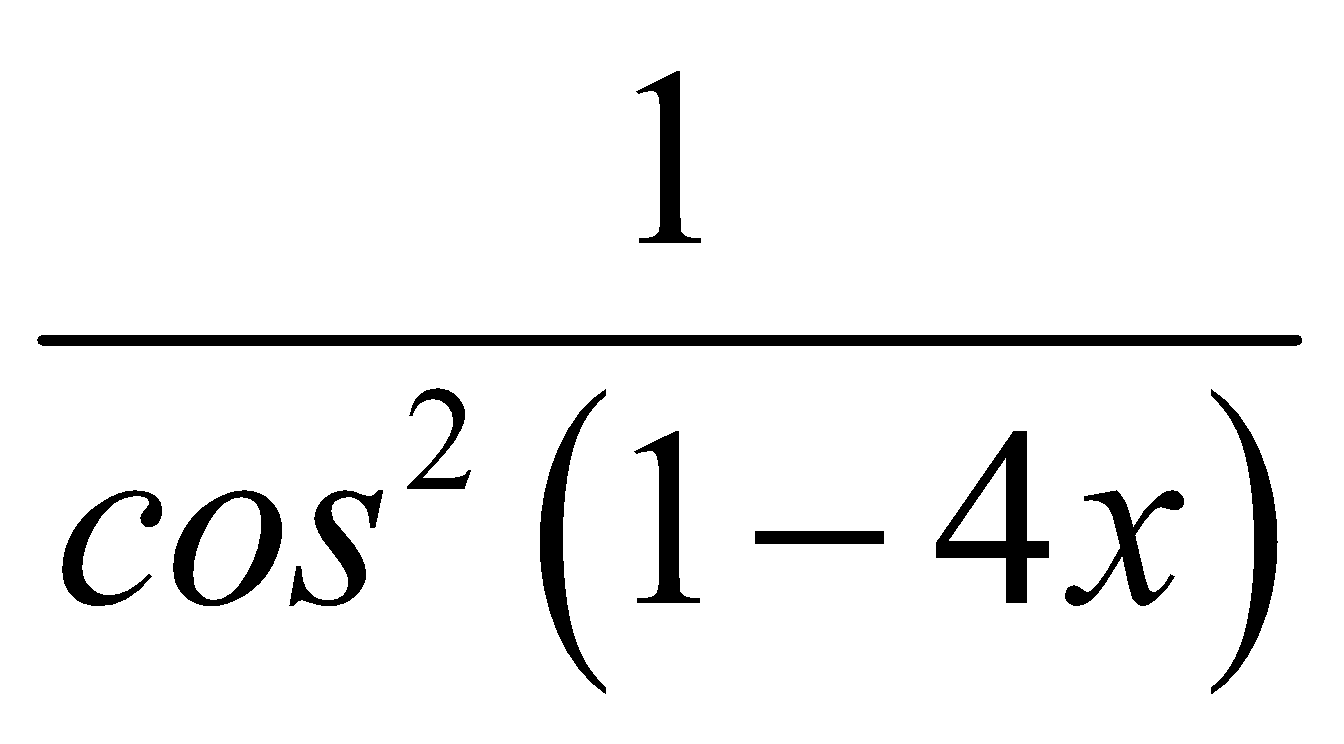
C. y′ = 2tan(1−4x) +![]()
D. y′=−8cos2(1−4x)
Cho y = ![]() . Đạo hàm cấp 2 của y là:
. Đạo hàm cấp 2 của y là:
A. y′′ = ![]() (
(![]()
B. y′′ =![]()
C. y′′ =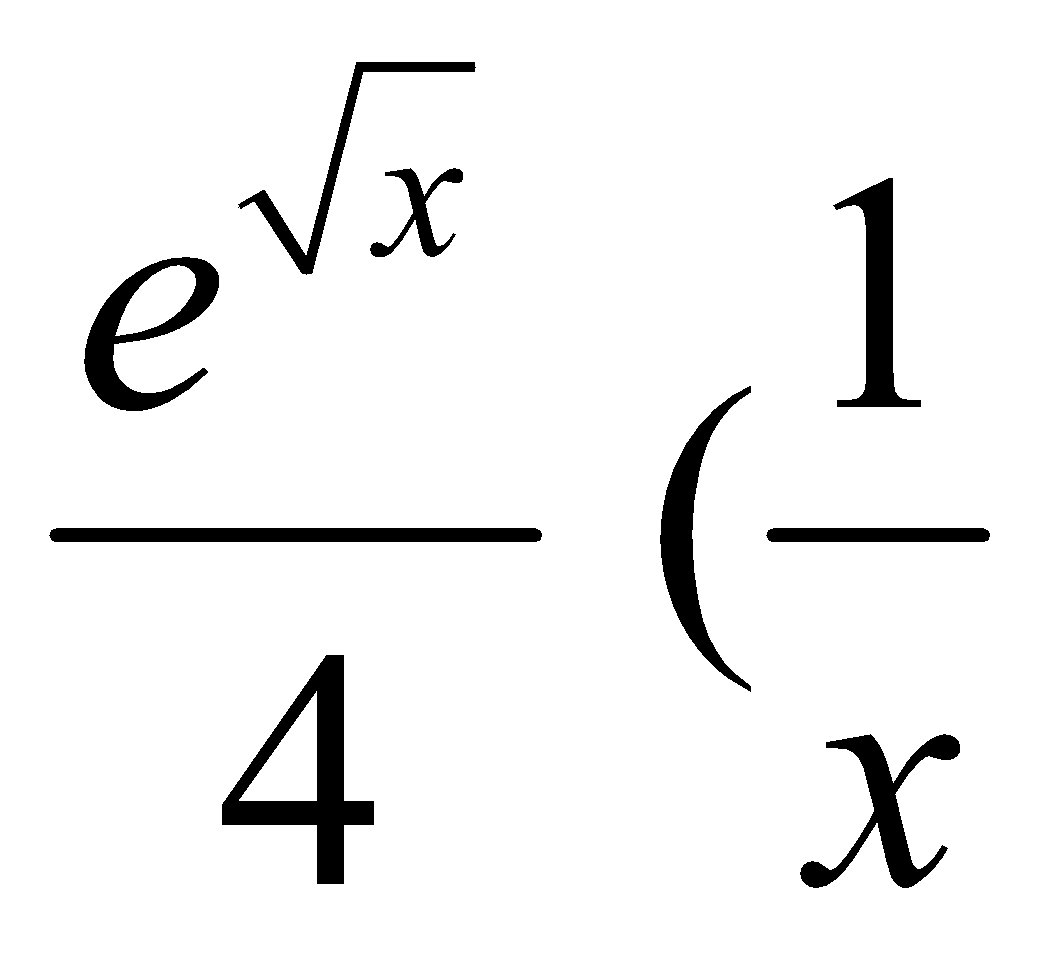 -
- ![]() )
)
D. y′′ = 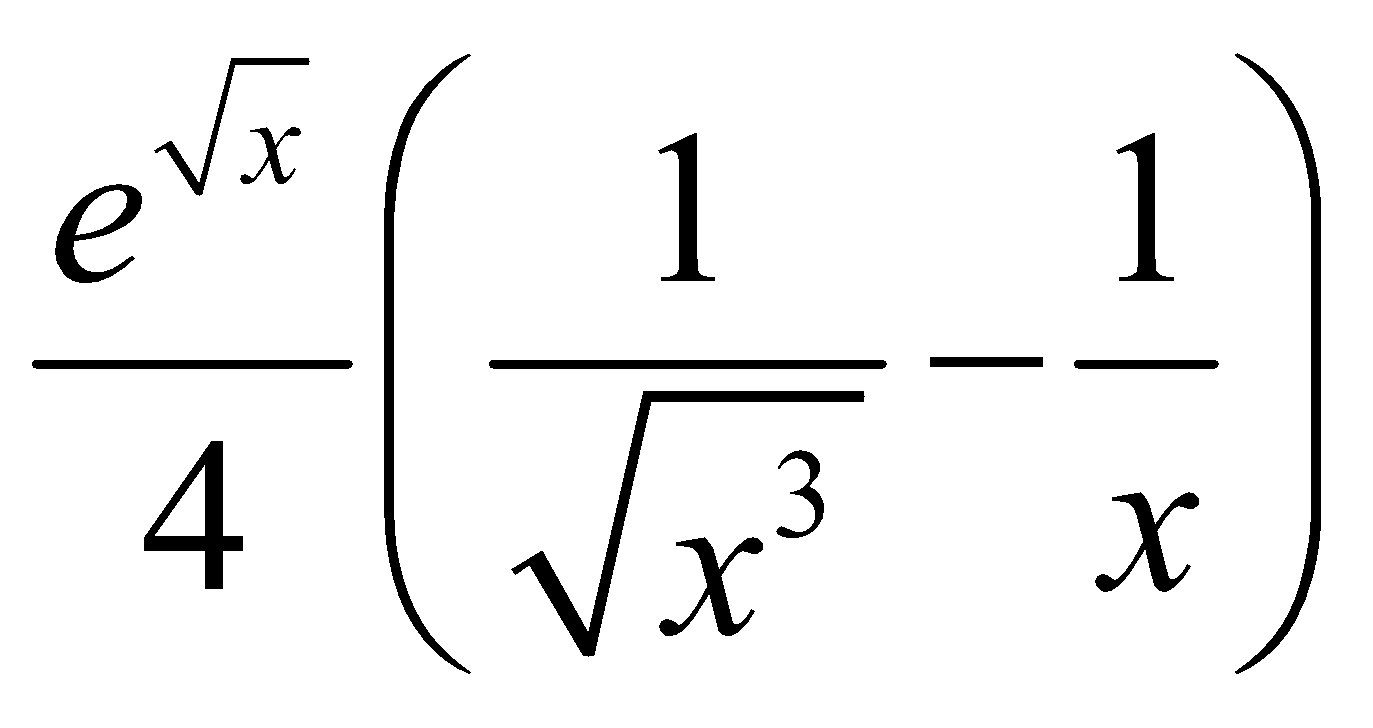
Cho hàm số y=sin(cosx). Đạo hàm y′ là :
A. y′=cos(cos x)
B. y′=−sinxsin(cos x)
C. y′=sin(−cos x)
D. y′=−sinxcos(cos x)
Đạo hàm của y = x2 . ![]() là:
là:
A. y’ = 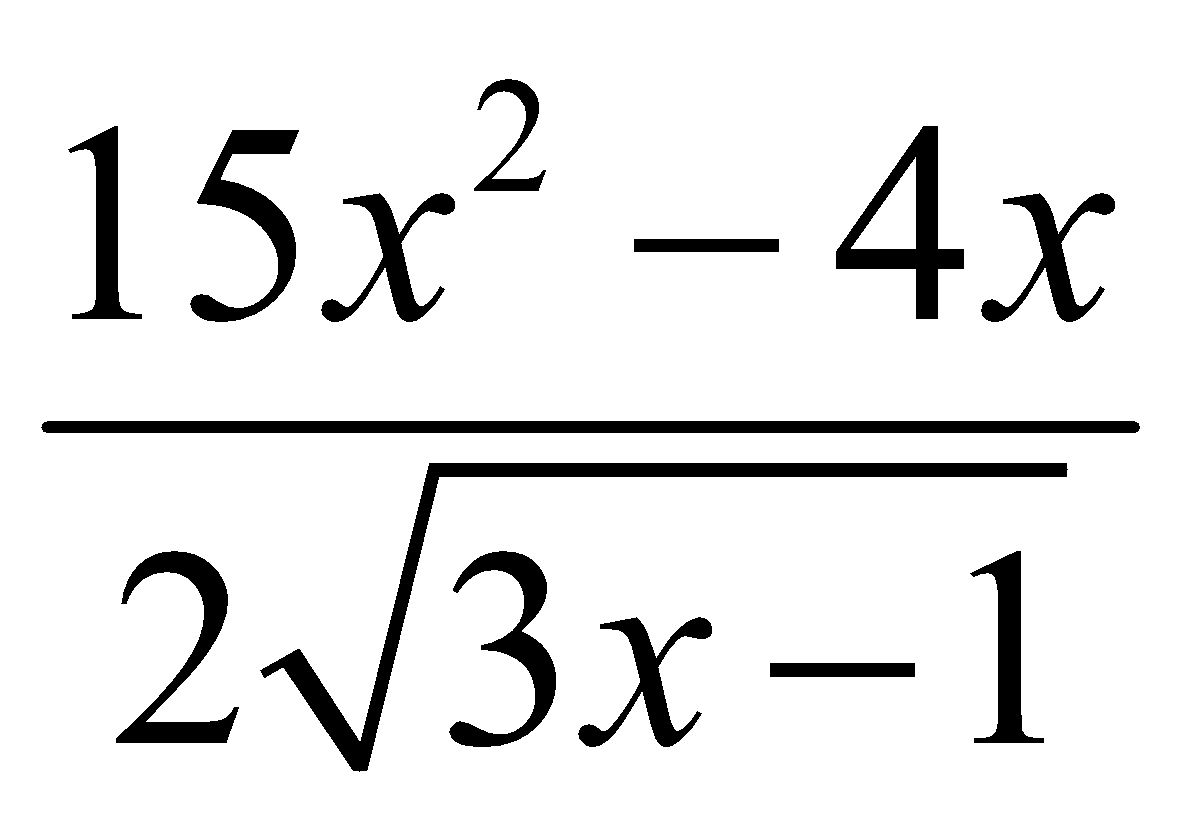
B. y’ =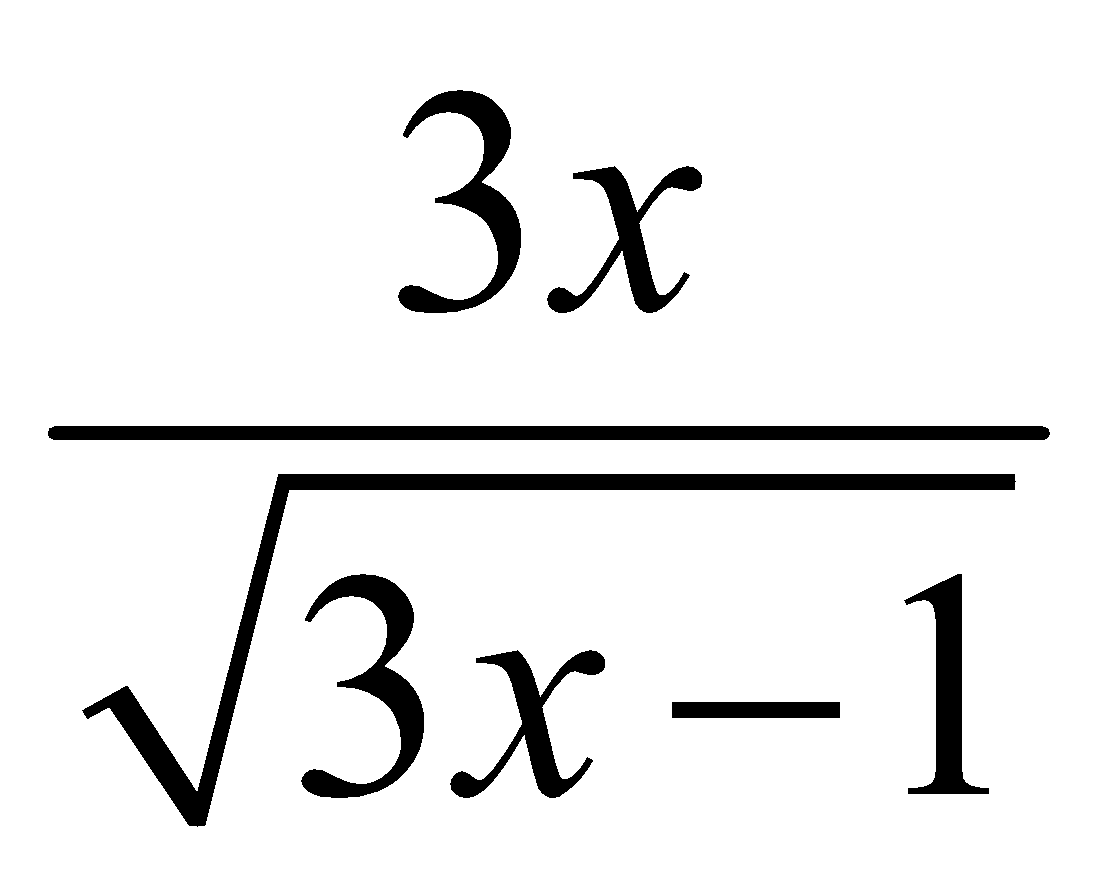
C. y’ =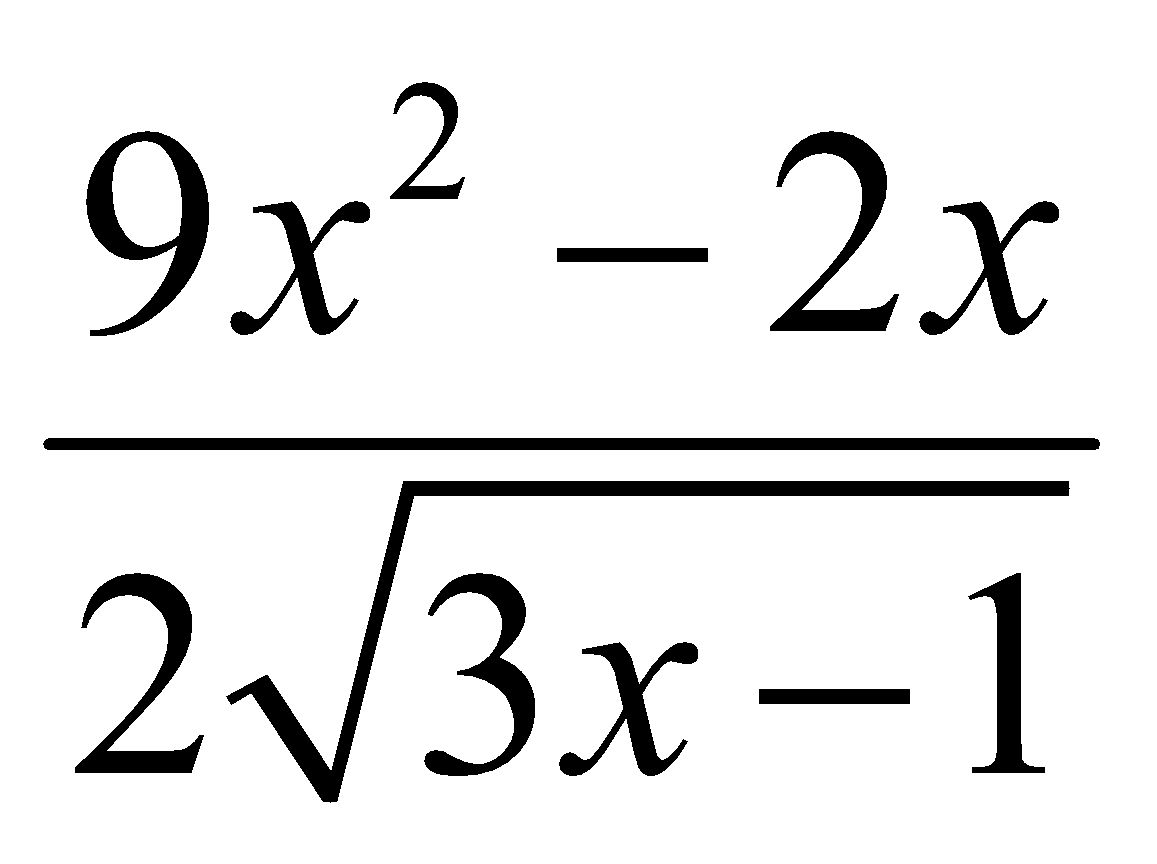
D. y’ = ![]()
Cho hàm số y = ![]() . Giá trị lớn nhất của hàm số là:
. Giá trị lớn nhất của hàm số là:
A. 0
B. 1
C. ![]()
D. ![]()
Cho hàm số y = (-3x +5). ![]() . Hàm số tăng trên:
. Hàm số tăng trên:
A. (![]() )
)
B. (-![]() và (
và (![]() , +
, +![]()
C.![]() ,
, ![]() )
)
D. (-![]() ) và (
) và (![]() , +
, +![]()
Cho hàm (x2 – 3x +2) . ![]() . Hàm số giảm trên:
. Hàm số giảm trên:
A. 2 khoảng (-![]() và (2 +
và (2 + ![]() , +
, +![]()
B. (2 +![]() , +
, +![]() )
)
C. (-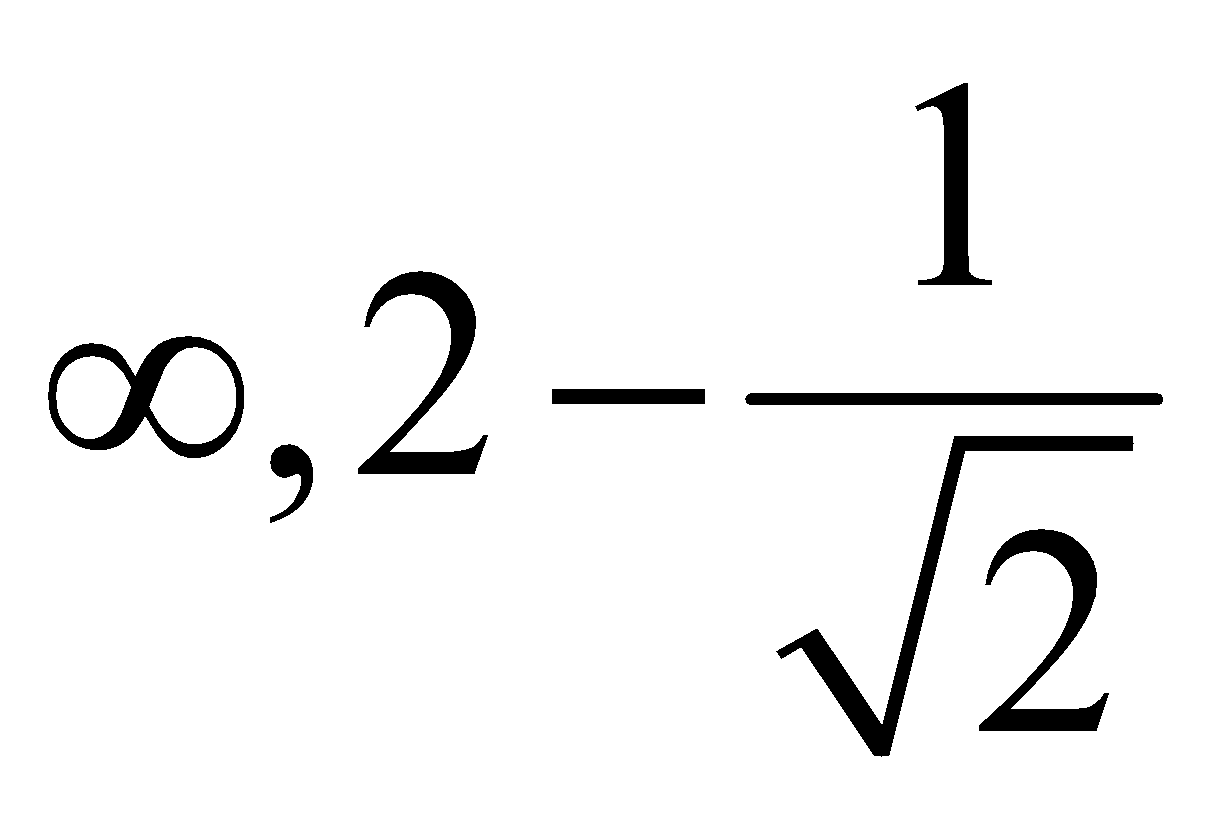 )
) ![]() )
)
D. (2 - ![]() , 2 +
, 2 + ![]() )
)
Cho hàm số y = x.ln2x. Số điểm dừng của hàm số là :
A. 3
B. 1
C. 4
D. 2
Cho hàm số y = (x2 – 5x +4)10. Hàm số tăng trên:
A. (1, ![]() ) và (4, +
) và (4, +![]()
B. (-![]()
C. (1,4)
D. (-![]()
Đường mức của hàm số w = x2 + 3y2 - x ứng với mức w0 = 1 có phương trình là :
A. x2 + 3y2 –x = 0
B. x2 + 3y2 – x = 2
C. x2 + 3y2 – x = 1
D. x2 + 3y2 – x = -1
Giá trị của hàm số x2 + 2xy – 3y2 tại điểm (1, -1) là :
A. –4
B. 0
C. 6
D. 4
Đạo hàm riêng theo biến y của hàm số w = 4x2 + 3xy – y2 tại điểm (1, 2) là:
A. 10
B. 9
C. –9
D. 14
Với hàm sản xuất dạng Cobb – Douglas Q=a.Kα Lβ(a, α, β>0) , theo quy luật lợi ích cận biên giảm dần các tham số α, β phải thỏa mãn điều kiện:
A. α≤1,β≤1
B. α≤0,β≤0
C. α≥0,β≥0
D. α≥1,β≥1
Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3x2 + y2 = 28. Hàm Lagrange L = 3x + 2y + λ (28 – 3x2 – y2) có các đạo hàm riêng cấp 1 Lx’ = 3 – 6 λx; Lx’ = 2 – 2 λy. Hàm số L có điểm dừng là M0 (x0, y0, λ0) với λ0 = ![]() và:
và:
A. x0 = 4; y0 = 2
B. x0 = 2; y0 = 4
C. x0 = -2; y0 = -4
D. x0 = -4; y0 = -2
Sử dụng phương pháp nhân tử Lagrange giải bài toán tìm cực trị có điều kiện, ta biết rằng hàm Lagrange L có điểm dừng M0 (x0, y0, -12) và L’xx = -2 λ; Lyx’’ = 0 ; L’’yy = -4 λ; gy’ = 1. Khi đó tại điểm (x0, y0), hàm số với điều kiện đã cho:
A. đạt giá trị cực đại.
B. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của x0, y0
C. không đạt cực trị.
D. đạt giá trị cực tiểu.
Xét hàm số 2 biến số w = f(x, y). Ký hiệu: D = 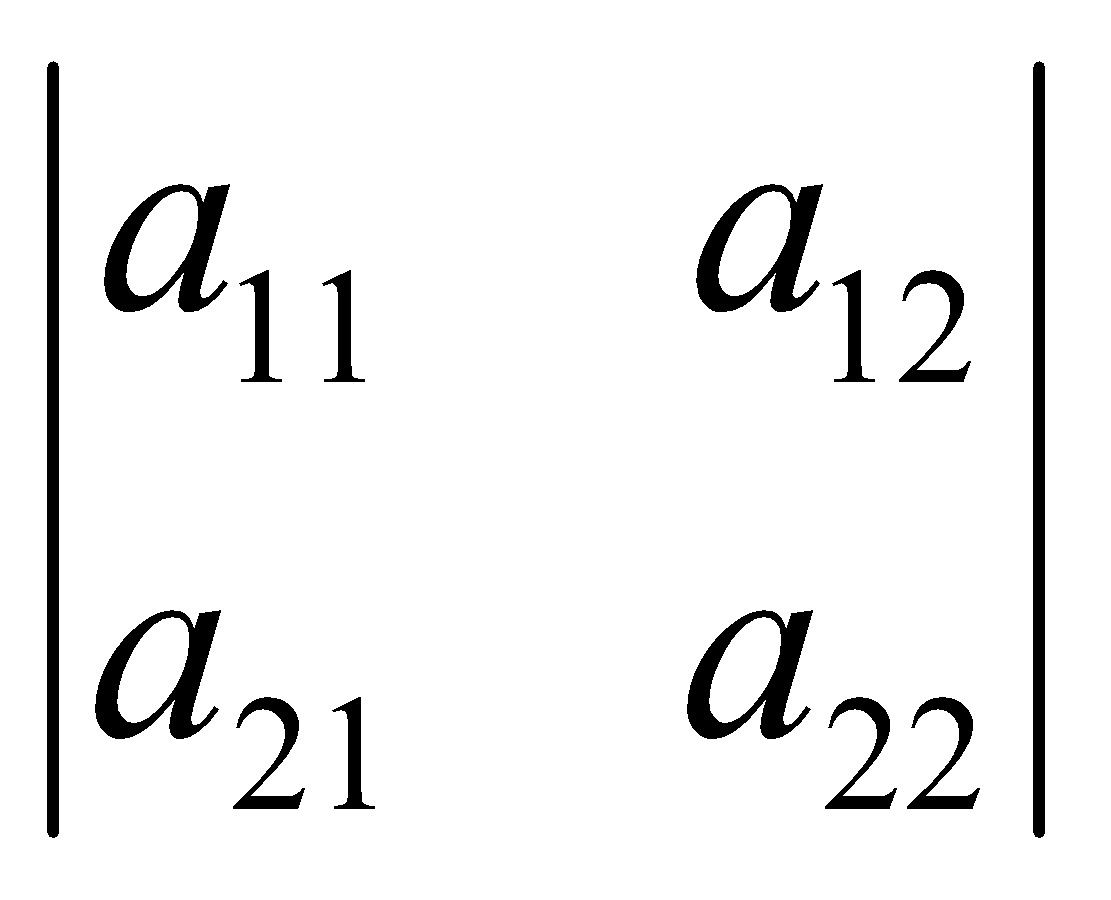 = a11. a22 – a12. a21 với a11, a12, a21, a22 lần lượt là giá trị của các đạo hàm riêng cấp 2 wxx’’, wxy’’, wyy’’ tính tại điểm dừng M0 (x0, y0). Khi đó nếu D>0 thì theo điều kiện đủ của cực trị, điểm M0 (x0, y0):
= a11. a22 – a12. a21 với a11, a12, a21, a22 lần lượt là giá trị của các đạo hàm riêng cấp 2 wxx’’, wxy’’, wyy’’ tính tại điểm dừng M0 (x0, y0). Khi đó nếu D>0 thì theo điều kiện đủ của cực trị, điểm M0 (x0, y0):
A. không là điểm cực trị của hàm số.
B. là điểm cực đại của hàm số.
C. là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a11
D. là điểm cực tiểu của hàm số.
Khi giả bài toán tìm cực trị của hàm số w = x2 + y2 với điều kiện ràng buộc là phương trình 3x + 2y = 26, hàm Lagrange L có điểm dừng là M0 (x0, y0, λ0) với y0 = λ0 và x0 có giá trị là:
A. 6
B. 4
C. ![]()
D. 2
Tính tích phân: ![]()
A.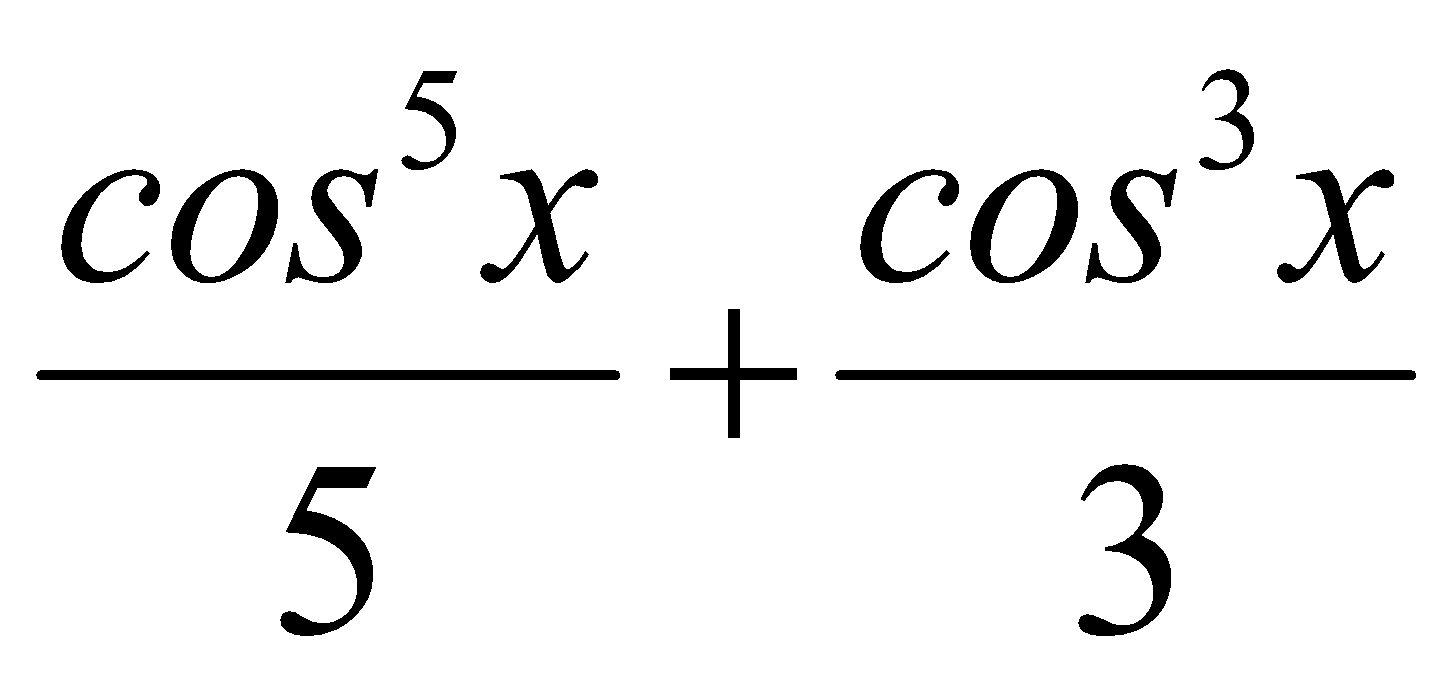 + C
+ C
B. 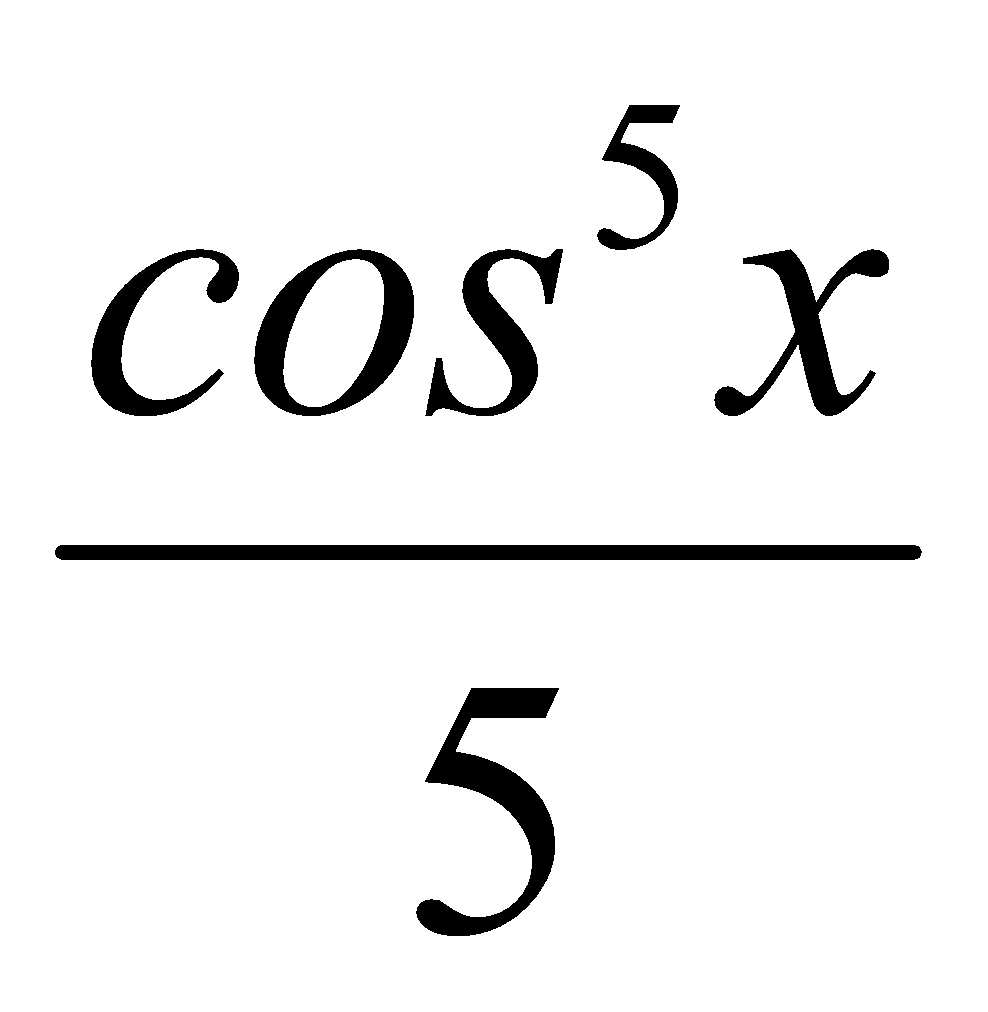 -
- 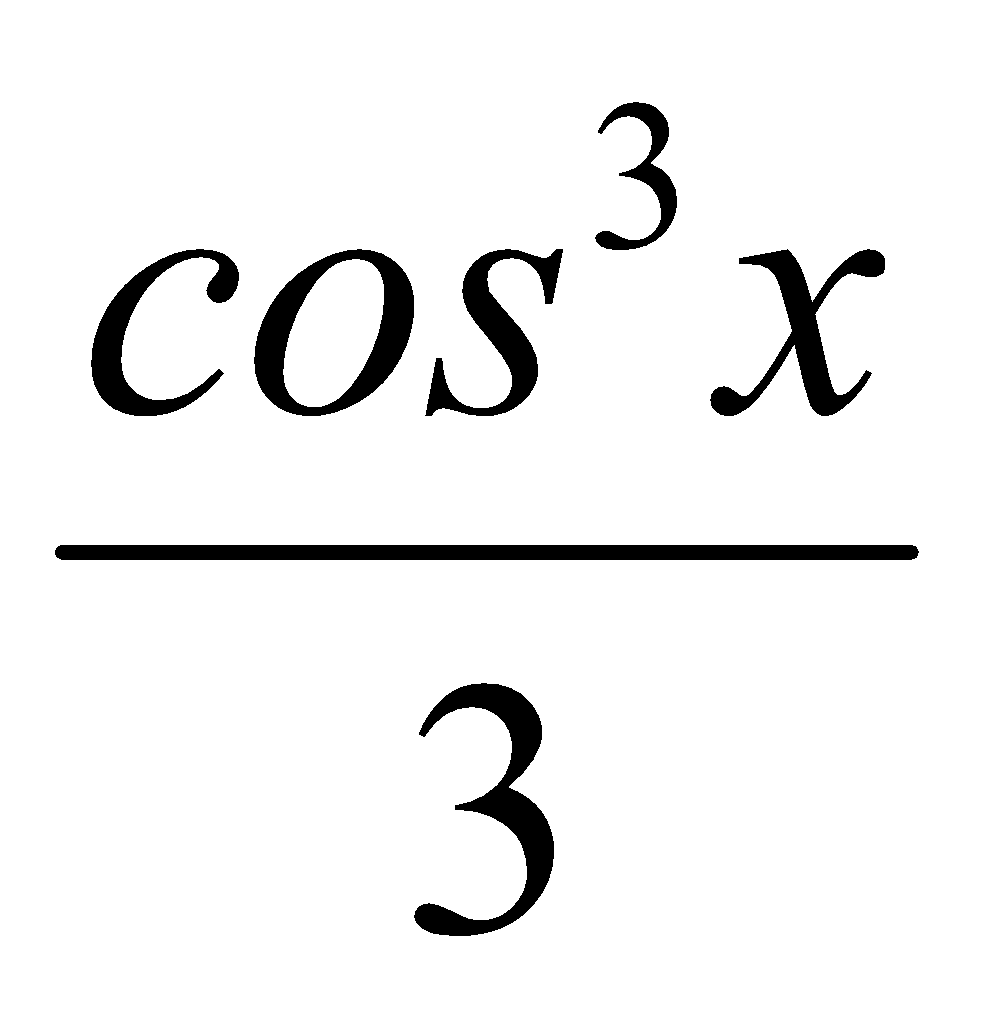 + C
+ C
C. 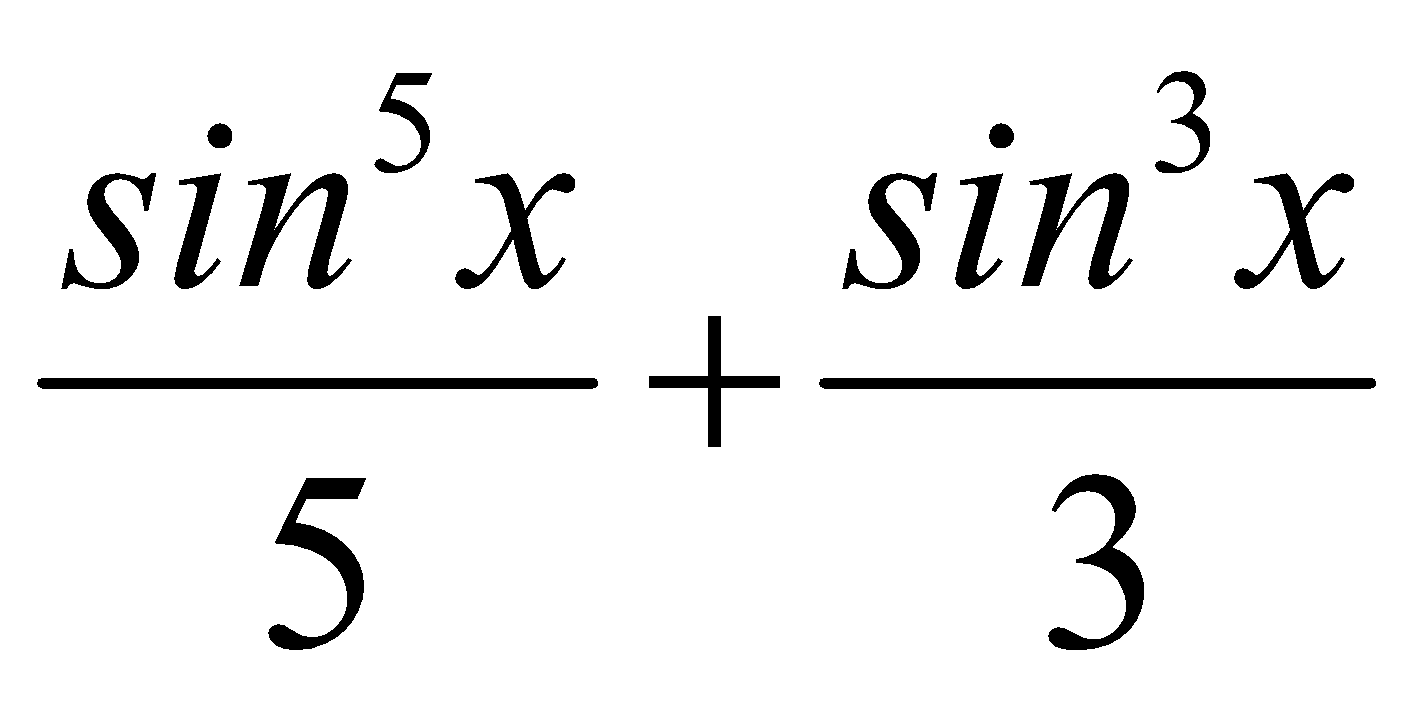 + C
+ C
D. ![]() -
- ![]() + C
+ C
Kết quả đúng của tích phân: I = ![]() .lnx.dx:
.lnx.dx:
A. 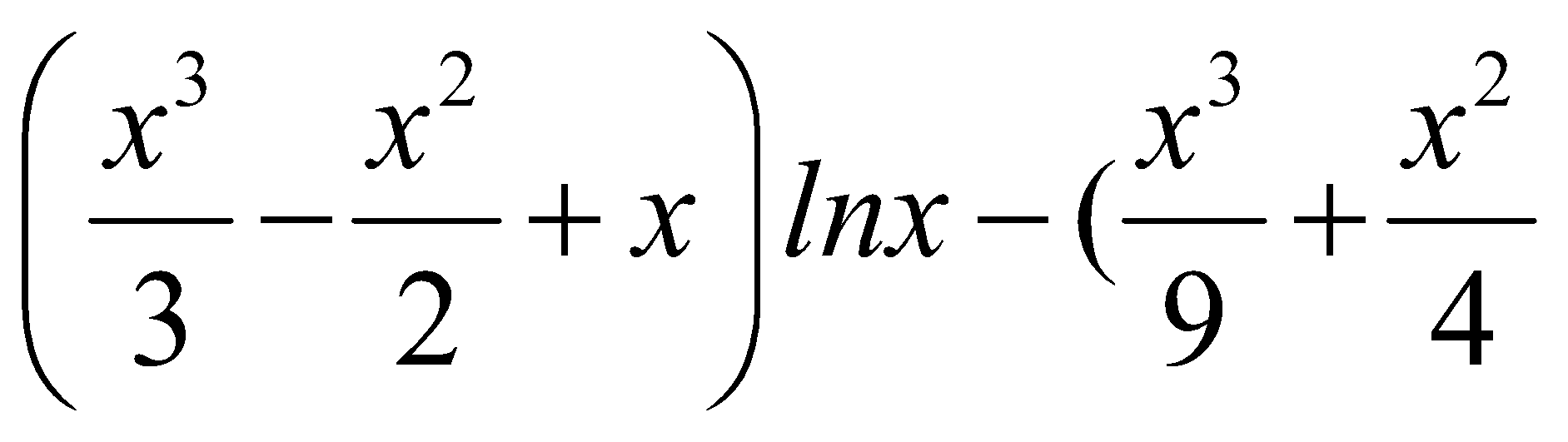 +x) + C
+x) + C
B. (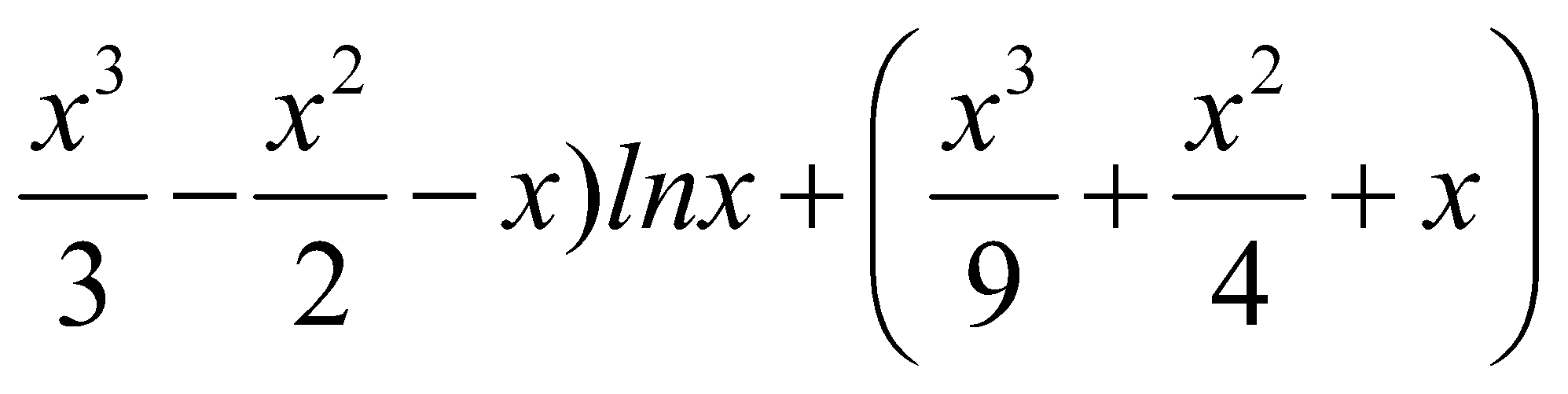 + C
+ C
C. ![]()
D. 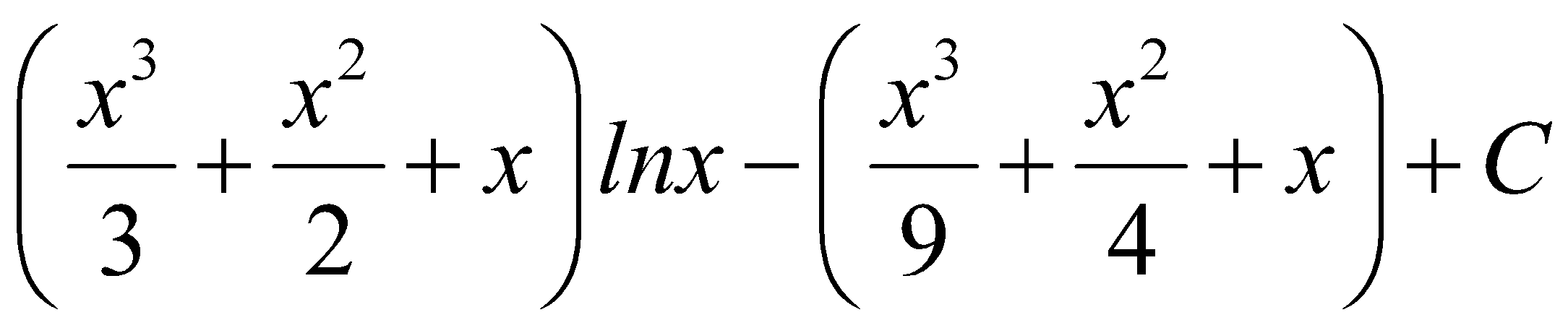
Tính tích phân: ![]()
A. ex. ![]() + C
+ C
B. –ex. ![]() + C
+ C
C. ex. ![]() + C
+ C
D. ex. ![]() + C
+ C
Tính tích phân 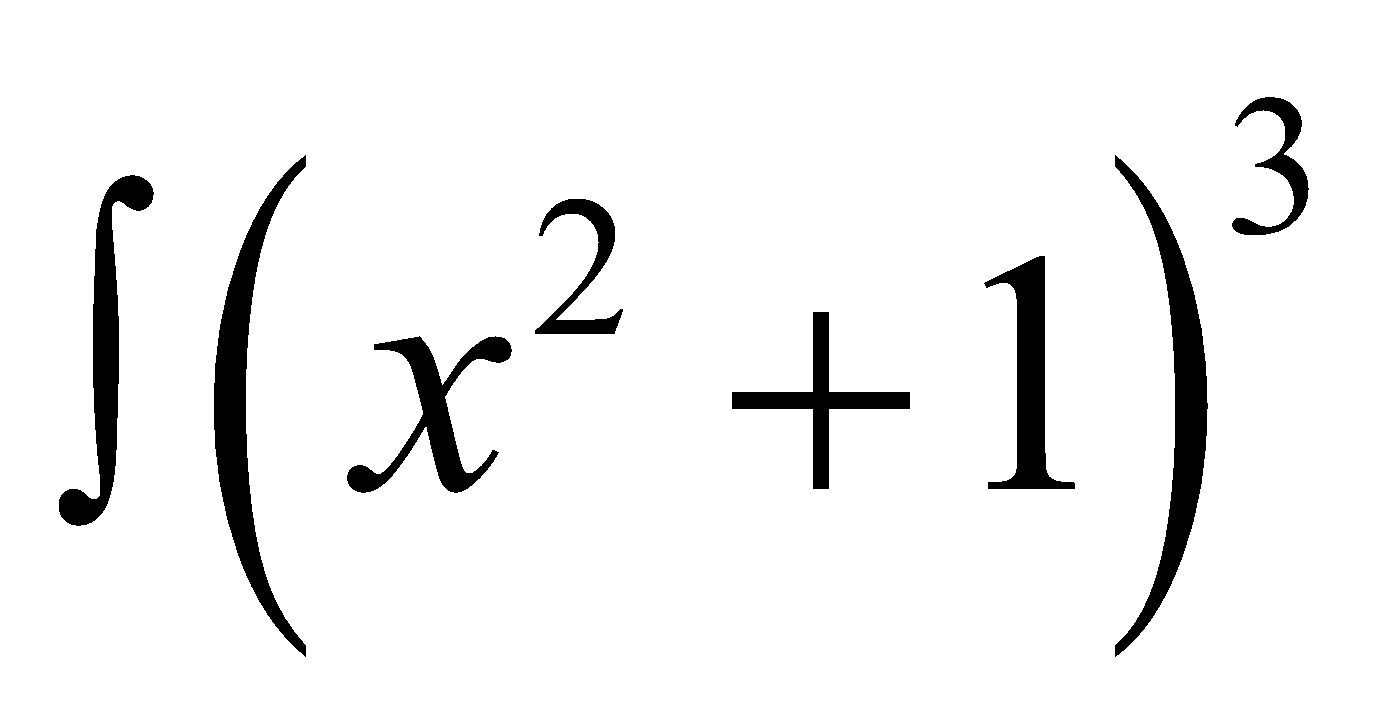 . dx
. dx
A. ![]()
B.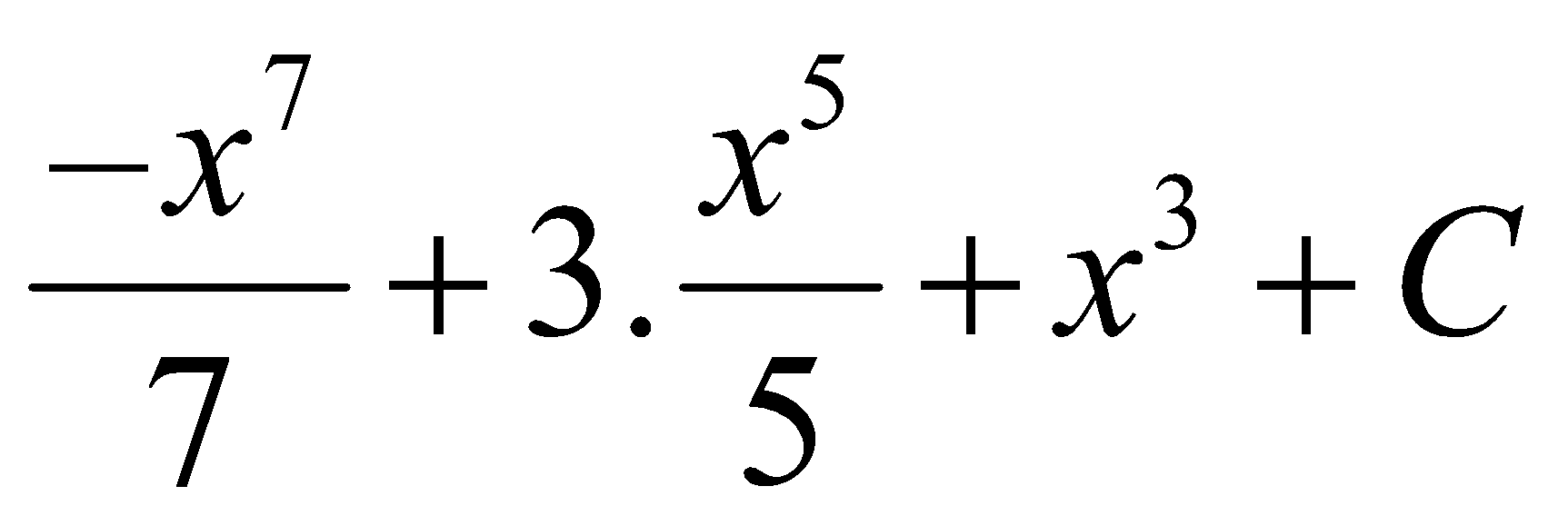
C.![]()
D.