Quiz

Đề kiểm tra 45 phút Toán 12 Chương 1 Hình học có đáp án (Đề 2)

Admin14 câu hỏiToánLớp 12

Bắt đầu ngay

14 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Có bao nhiêu khối đa diện đều?

A. 4.

B. 5.

C. 3.

D. 2.

2. Nhiều lựa chọn

Khái niệm nào sau đây đúng với khối chóp?

A. là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.

B. là phần không gian được giới hạn bởi hình chóp và cả hình chóp đó.

C. là phần không gian được giới hạn bởi hình chóp.

D. là khối đa diện có hình dạng là hình chóp.

3. Nhiều lựa chọn

Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất

A. Năm cạnh

B. Bốn cạnh

C. Ba cạnh

D. Hai cạnh

4. Nhiều lựa chọn

Hình chóp tứ giác đều có mấy trục đối xứng?

A. Không có

B. 1

C. 2

D. 3

5. Nhiều lựa chọn

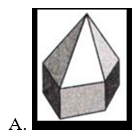
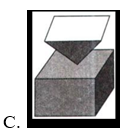
Trong các hình dưới đây, hình nào là khối đa diện?

6. Nhiều lựa chọn

Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành 4 khối tứ diện:

A. AMCN, AMND, BMCN, BMND

B. AMCN, AMND, AMCD, BMCN

C. BMCD, BMND, AMCN, AMDN

D. AMCD, AMND, BMCN, BMND

7. Nhiều lựa chọn

Số mặt phẳng đối xứng của tứ diện đều là:

A. 4.

B. 8.

C. 6.

D. 10.

8. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có 1 mặt phẳng đối xứng là?

A. (SAC)

B. (SAB)

C. (ABCD)

D. (SAD)

9. Nhiều lựa chọn

Cho hình chóp S.ABC, gọi M; N lần lượt là trung điểm của SA; SB. Tính tỉ số $\frac{V_{S . A B C}}{V_{S . M N C}}$

A. $\frac{1}{2}$

B. 4

C. 2

D. $\frac{1}{4}$

10. Nhiều lựa chọn

Tính thể tích khối tứ diện đều cạnh a?

A. $\frac{a^{3} \sqrt{2}}{12}$

B. $\frac{a^{3} \sqrt{2}}{4}$

C. $a^{3}$

D. $\frac{a^{3}}{6}$

11. Nhiều lựa chọn

Cho lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại A. Hình chiếu của A’ lên (ABC) là trung điểm của BC. Tính thể tích khối lăng trụ ABC.A'B'C' biết $A B = a, A C = a \sqrt{3}, A A' = 2 a$

A. $\frac{a^{3}}{2}$

B. $\frac{3 a^{3}}{2}$

C. $a^{3} \sqrt{3}$

D. $3 a^{3} \sqrt{3}$

12. Nhiều lựa chọn

Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng $a \sqrt{3} v à \hat{B C D} = 120 °$ . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chop S.ABCD.

A. $\frac{\sqrt{3} a^{3}}{12}$

B. $\frac{3 \sqrt{3} a^{3}}{2}$

C. $\frac{\sqrt{3} a^{3}}{4}$

D. $\frac{3 \sqrt{3} a^{3}}{4}$

13. Nhiều lựa chọn

Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh $A B = a, A D = a \sqrt{2}, S A ⊥ (A B C D)$ góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:

A. $\sqrt{2} a^{3}$

B. $\sqrt{6} a^{3}$

C. $3 a^{3}$

D. $3 \sqrt{2} a^{3}$

14. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.

A. $V = \frac{a^{3}}{24}$

B. $V = \frac{3 a^{3}}{24}$

C. $V = \frac{a^{3} \sqrt{3}}{24}$

D. $V = \frac{a^{3} \sqrt{2}}{24}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube