24 CÂU HỎI
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x - y + 3 = 0\]. Vec-tơ nào sau đây không là vecto pháp tuyến của mặt phẳng (P) .
A.\[\vec a = (3, - 3,0)\]
B. \[\vec a = (1, - 2,3)\]
C. \[\vec a = ( - 1,1,0)\]
D. \[\vec a = (1, - 1,0)\]
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận \[\overrightarrow n = \left( { - 2,4,1} \right)\;\]làm vectơ pháp tuyến.
A.\[2x - 3y + 4z + 12 = 0\]
B. \[2x - 4y - z - 12 = 0\]
C. \[2x - 4y - z + 10 = 0\]
D. \[ - 2x + 4y + z + 11 = 0\]
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng \[(P):2x - y + 3z + 4 = 0\] là:
A.\[2x - y + 3z + 7 = 0\]
B. \[2x + y - 3z + 7 = 0\]
C. \[x - 3y + 2z + 7 = 0\]
D. \[2x - y + 3z - 7 = 0\]
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2), B(2,−3,−2). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
A.\[x + y + 2z - 1 = 0\]
B. \[2x + y + z - 1 = 0\]
C. \[x + y + 2z = 0\]
D. \[x + y + 2z + 1 = 0\]
Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
A.\[ - x - 3y = 0\]
B. \[3x + y + 3z - 6 = 0\]
C. \[15x - y - 3z - 12 = 0\]
D. \[15x - y - 3z - 12 = 0\]
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1) . Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
A.\[x + y + z = 0\]
b. \[2x + y + z - 2 = 0\]
C. \[x + 2y + z - 2 = 0\]
D. \[x + y + z - 1 = 0\]
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với \[\left( Q \right):x + 2y - 3z + 1 = 0\;\]và \[\left( R \right):2x - 3y + z + 1 = 0\;\].
A.\[2x + 4y + z = 0\]
B. \[x + 2y - z - 3 = 0\]
C. \[x + y + z + 1 = 0\]
D. \[x + y + z - 1 = 0\]
Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng \[\left( P \right):x + 2y + 2z + 11 = 0\;\]và \[\left( Q \right):x + 2y + 2z + 2 = 0\;\]. Tính khoảng cách giữa (P) và (Q).
A.9
B.6
C.5
D.3
Viết phương trình mặt phẳng (P) song song với mặt phẳng \[\left( Q \right):x + y - z - 2 = 0\;\]và cách (Q) một khoảng là \(2\sqrt 3 \).
A.\[x + y - z + 4 = 0\;\] hoặc \[x + y - z - 8 = 0\;\].
B.\[x + y - z - 4 = 0\;\] hoặc \[x + y - z + 8 = 0\;.\]
C.\[x + y - z + 4 = 0\;\] hoặc \[x + y - z + 8 = 0\;\].
D.\[x + y - z - 4 = 0\;\] hoặc \[x + y - z - 8 = 0\;\].
Trong không gian Oxyz, cho hai mặt phẳng \[\left( P \right):3x - my - z + 7 = 0,\left( Q \right):6x + 5y - 2z - 4 = 0.\] Hai mặt phẳng (P và (Q) song song với nhau khi m bằng
A.\[m = 4\]
B. \[m = - \frac{5}{2}\]
C. \[m = - 30\]
D. \[m = \frac{5}{2}\]
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \[\left( P \right):mx + y - 2z - 2 = 0\;\]và \[\left( Q \right):x - 3y + mz + 5 = 0\]. Tìm tất cả các giá trị thực của m để hai mặt phẳng đã cho vuông góc với nhau.
A.m=−2
B.m=3
C.m=−3
D.m=2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[\left( P \right):ax + by + cz - 27 = 0\;\]qua hai điểm A(3,2,1),B(−3,5,2) và vuông góc với mặt phẳng \[\left( Q \right):3x + y + z + 4 = 0\;\]. Tính tổng \[S = a + b + c.\]
A.S=−2
B.S=2
C.S=−4
D.S=−12
Trong hệ trục toạ độ không gian Oxyz, cho \[A\left( {1,0,0} \right),B\left( {0,b,0} \right),C\left( {0,0,c} \right),\] biết b,c>0, phương trình mặt phẳng \[\left( P \right):y - z + 1 = 0\;\]. Tính \[M = c + b\] biết \[\left( {ABC} \right) \bot \left( P \right),\;d\left( {O,\left( {ABC} \right)} \right) = \frac{1}{3}\]
A.2
B. \(\frac{1}{2}\)
C. \[\frac{5}{2}\]
D. 1
Cho mặt phẳng (P) có phương trình \[x + 3y - 2z + 1 = 0\;\] và mặt phẳng (Q) có phương trình \[x + y + 2z - 1 = 0\]. Trong các mặt phẳng tọa độ và mặt phẳng (Q) , xác định mặt phẳng tạo với (P) góc có số đo lớn nhất.
A.Mặt phẳng (Oxy)
B.Mặt phẳng (Oyz)
C.Mặt phẳng (Oxz)
D.Mặt phẳng (Q)
Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho\[M{A^2} - M{B^2} = 2\]. Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình \[x - 3y + 4z - 5 = 0\].
B.(S) là mặt phẳng có phương trình \[x - 3y + 4z - 2 = 0\].
C.(S) là mặt phẳng có phương trình \[x - 3y + 4z + 4 = 0\].
D.(S) là mặt phẳng có phương trình \[x - 3y + 4z - 3 = 0\].
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình \[x + 2y - 2z + 1 = 0\;\] và \[x - 2y + 2z - 1 = 0\]. Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q). Tìm khẳng định đúng.
A.(S) là mặt phẳng có phương trình x=0.
B.(S) là mặt phẳng có phương trình \[2y - 2z + 1 = 0\].
C.(S) là đường thẳng xác định bởi giao tuyến của hai mặt phẳng có phương trình x=0 và \[2y - 2z + 1 = 0.\]
D.(S) là hai mặt phẳng có phương trình x=0x=0 và \[2y - 2z + 1 = 0.\]
Với mỗi giá trị của tham số m, xét mặt phẳng (Pm) xác định bởi phương trình \[mx + m\left( {m + 1} \right)y + {\left( {m - 1} \right)^2}z - 1 = 0\]. Tìm tọa độ của điểm thuộc mọi mặt phẳng (Pm).
A. (1,−2,1)
B.(0,1,1)
C.(3,−1,1)
D.Không có điểm như vậy.
Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng \[(Q):19x - 6y - 4z + 27 = 0\;\]và \[(R):42x - 8y + 3z + 11 = 0\;\]là:
A.\[3x + 2y + 6z - 23 = 0\]
B. \[3x - 2y + 6z - 23 = 0\]
C. \[3x + 2y + 6z + 23 = 0\]
D. \[3x + 2y + 6z - 12 = 0\]
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
A.\[2x - y + 3z + 20 = 0\]
B. \[2x - y + 3z + 12 = 0\]
C. \[2x - y + 3z - 20 = 0\]
D.\[2y + y - 3z + 20 = 0\]
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x′Ox,y′Oy,z′Oz lần lượt tại các điểm A,B,C sao cho \[OA = OB = OC \ne 0\]?
A.3.
B.1.
C.4.
D.8.
Cho mặt phẳng \[\left( \alpha \right)\;\]đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng \[\left( \alpha \right)\;\]tạo với mặt phẳng (Oyz) một góc bằng 600. Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng \[\left( \alpha \right)\]
A.1
B.\[\frac{3}{2}\]
C. \[\frac{2}{{\sqrt 3 }}\]
D. 2
Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng (A′BC) và (ABC′) bằng:
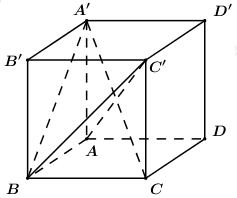
A.\[\frac{{\sqrt 3 }}{2}\]
B. \[\frac{{\sqrt 2 }}{2}\]
C. 0
D. \[\frac{1}{2}\]
Trong không gian Oxyz, hai mặt phẳng \[4x - 4y + 2z - 7 = 0\;\]và \[2x - 2y + z + 4 = 0\;\]chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:
A.\[V = \frac{{125}}{8}\]
B. \[V = \frac{{81\sqrt 3 }}{8}\]
C. \[V = \frac{{9\sqrt 3 }}{2}\]
D. \[V = \frac{{27}}{8}\]
Trong không gian Oxyz, cho ba mặt phẳng \[\left( P \right):x + y + z - 1 = 0,\;\left( Q \right):2x + my + 2z + 3 = 0\;\]và \[\left( R \right): - x + 2y + nz = 0\]. Tính tổng \[m + 2n\], biết \[\left( P \right) \bot \left( R \right)\;\]và \[\left( P \right)//\left( Q \right)\]
A. -6
B. 1
C. 0
D. 6

