30 CÂU HỎI
Hàm số \[y = {\log _a}x(0 < a \ne 1)\] xác định trên:
A.(0;1)
B.R
C.\[R \setminus \left\{ 0 \right\}\]
D. \[\left( {0; + \infty } \right)\]
Hàm số \[y = {\log _a}x\] có đạo hàm là:
A.\[y' = {\log _a}x\]
B. \[y' = x\ln a\]
C. \[y' = \frac{1}{{x\ln a}}\]
D. \[y' = \frac{1}{x}\ln a\]
Chọn mệnh đề đúng:
A.\[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1\]
B. \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 - x} \right)}}{x} = 1\]
C. \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln x}}{x} = 1\]
D. \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{{1 + x}} = 1\]
Tiệm cận đứng của đồ thị hàm số \[y = {\log _a}x(0 < a \ne 1)\] là đường thẳng:
A.x=1
B.y=0
C.y=1
D.x=0
Điểm \[({x_0};{y_0})\;\]thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\] nếu:
A.\[{y_0} = {\log _a}{x_0}\]
B. \[{y_0} = x_0^a\]
C. \[{y_0} = {a^{{x_0}}}\]
D. \[{x_0} = {\log _a}{y_0}\]
Điểm nào sau đây không thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\]?
A.\[\left( {1;0} \right)\]
B. \[\left( {a,1} \right)\]
C. \[\left( {{a^2};a} \right)\]
D. \[\left( {{a^2};2} \right)\]
Cho hàm số \[y = {\log _{\frac{\pi }{4}}}x\]. Khẳng định nào sau đây sai?
A.Hàm số đã cho nghịch biến trên tập xác định
B.Đồ thị hàm số đã cho có một tiệm cận đứng là trục Oy
C.Hàm số đã cho có tập xác định \[D = \left( {0; + \infty } \right)\;\]
D.Đồ thị hàm số đã cho luôn nằm phía trên trục hoành.
Gọi (C) là đồ thị hàm số y=logx. Tìm khẳng định đúng?
A.Đồ thị (C) có tiệm cận đứng
B.Đồ thị (C) có tiệm cận ngang.
C.Đồ thị (C) cắt trục tung.
D.Đồ thị (C) không cắt trục hoành.
Trong các khẳng định sau, khẳng định nào đúng?
A.\[log\left( {a + b} \right) = \log a + \log b;\forall a > 0;b > 0\]
B.\[{a^{x + y}} = {a^x} + {a^y};\,\forall a > 0;\,x,y \in \,R\]
C.Hàm số \[y = {e^{10x + 2017}}\] đồng biến trên R
D.Hàm số \[y = {\log _{12}}x\] nghịch biến trên khoảng \[(0; + \infty )\]
Cho a,b là các số thực, thỏa mãn 0<a<1<b, khẳng định nào sau đây là đúng?
A.\[{\log _b}a + {\log _a}b < 0\]
B. \[{\log _b}a > 1\]
C. \[{\log _a}b > 0\]
D. \[{\log _a}b + {\log _b}a \ge 2\]
Cho \[a > 0,a \ne 1\]. Tìm mệnh đề đúng trong các mệnh đề sau:
A.Tập xác định của hàmsố \[y = {a^x}\]là \[\left( {0; + \infty } \right)\]
B.Tập giá trị của hàmsố \[y = {\log _a}x\] là tập R
C.Tập giá trị của hàmsố \[y = {a^x}\] là tập R
D.Tập xác định của hàmsố \[y = {\log _a}x\] là tập R
Tìm tập xác định D của hàm số \[y = {\log _{\sqrt 2 }}\left( {\frac{{ - 3}}{{2 - 2x}}} \right)\]
A.\[D = ( - \infty ;1)\]
B. \[D = [1; + \infty )\]
C. \[D = ( - \infty ;1]\]
D. \[D = (1; + \infty )\]
Đạo hàm hàm số \[y = {\log _{2018}}\left( {2018x + 1} \right)\] là:
A.\[\frac{1}{{x\ln 2018}}\]
B. \[\frac{{2018}}{{2018\left( {x + 1} \right)\ln 2018}}\]
C. \[\frac{1}{{\left( {2018x + 1} \right)\ln 2018}}\]
D.\[\frac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\]
Tính đạo hàm hàm số \[y = \ln \left( {1 + \sqrt {x + 1} } \right)\]
A.\[y' = \frac{1}{{2\sqrt {x + 1} \left( {1 + \sqrt {x + 1} } \right)}}\]
B. \[y' = \frac{1}{{1 + \sqrt {x + 1} }}\]
C. \[y' = \frac{1}{{\sqrt {x + 1} \left( {1 + \sqrt {x + 1} } \right)}}\]
D. \[y' = \frac{2}{{\sqrt {x + 1} \left( {1 + \sqrt {x + 1} } \right)}}\]
Cho a,b là các số thực dương, thỏa mãn \[{a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\] và \[{\log _b}\frac{1}{2} < {\log _b}\frac{2}{3}\]. Mệnh đề nào dưới đây đúng?
A.a > 1,0 < b < 1
B.0 < a < 1,0 < b < 1
C.0 < a < 1,b > 1
D.a > 1,b > 1
Hàm số nào trong các hàm số sau có đồ thị phù hợp với hình vẽ bên?
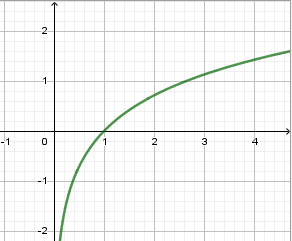
A.\[y = {e^x}\]
B. \[y = {\log _{0,5}}x\]
C. \[y = {e^{ - x}}\]
D. \[y = {\log _{\sqrt 7 }}x\]
Nếu gọi \[({G_1})\]là đồ thị hàm số \[y = {a^x}\;\] và \[({G_2})\]là đồ thị hàm số \[y = lo{g_a}x\;\] với \[0 < a \ne 1\]. Mệnh đề nào dưới đây đúng ?
A.\[({G_1})\]và \[({G_2})\] đối xứng với nhau qua trục hoành.
B. \[({G_1})\]và \[({G_2})\] đối xứng với nhau qua trục tung.
C. \[({G_1})\]và \[({G_2})\] đối xứng với nhau qua đường thẳng y = x.
D. \[({G_1})\]và \[({G_2})\] đối xứng với nhau qua đường thẳng y = −x.
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số \[y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\] được cho trong hình vẽ sau:
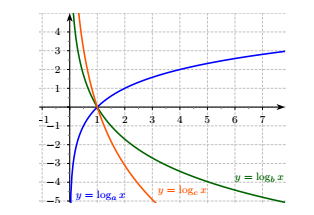
Mệnh đề nào dưới đây đúng?
A.a
B.b
C.a
D.c
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = log\left( {{x^2} - 2mx + 4} \right)\]có tập xác định là R
A.m<2
2
B.m=2
C.m<−2 hoặc m>2−2 hoặc m>
D.−2
Cho x,y là các số thực thỏa mãn \[{\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1\]. Tìm giá trị nhỏ nhất Pmin của biểu thức \[P = 2x - y.\]
A.\[{P_{\min }} = 4\]
B. \[{P_{\min }} = - 4\]
C. \[{P_{\min }} = 2\sqrt 3 \]
D. \[{P_{\min }} = \frac{{10\sqrt 3 }}{3}\]
Tìm tập giá trị T của hàm số \[f'\left( x \right) = \frac{{1 - \ln x}}{{{x^2}}}\] với \[x \in [1;{e^2}].\]
A.\[{\rm{T}} = \left[ {0;e} \right]\]
B. \[{\rm{T}} = \left[ {\frac{1}{e};e} \right]\]
C. \[{\rm{T}} = \left[ {0;\frac{1}{e}} \right]\]
D. \[{\rm{T}} = \left[ { - \frac{1}{e};e} \right]\]
Tìm tham số m để hàm số \[y = \frac{{{{\log }_{\frac{1}{2}}}x - 2}}{{{{\log }_2}x - m}}\] đồng biến trên khoảng (0;1).
A.m>0.
B.\[m \ge - 2\;\;\;\]
C.\[m \ge 0\]
D.m>−2.
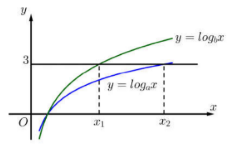
Hàm số \[y = {\log _a}x\]và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ \[{x_1},{x_2}\]. Biết rằng \[{x_2} = 2{x_1},\], giá trị của ab bằng:
A.\(\frac{1}{2}\)
B. \(\sqrt 3 \)
C. 2
D. \[\sqrt[3]{2}\]
Hàm số \[y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\] nghịch biến trên khoảng nào dưới đây?
A.\[\left( {1; + \infty } \right)\]
B. \[\left[ {1; + \infty } \right)\]
C. \[\left( {0; + \infty } \right)\]
D. \(\mathbb{R}\)
Tập xác định của hàm số \[f\left( x \right) = {\log _{\frac{1}{2}}}\left( {{{\log }_4}\left( {{{\log }_{\frac{1}{4}}}\left( {{{\log }_{16}}\left( {{{\log }_{\frac{1}{{16}}}}x} \right)} \right)} \right)} \right)\] là một khoảng có độ dài n/m, với m và n là các số nguyên dương và nguyên tố cùng nhau. Khi đó m−n bằng:
A.−240
B.271
C.241
D.−241
Cho hai hàm số \[y = \ln \left| {\frac{{x - 2}}{x}} \right|\]và\(y = \frac{3}{{x - 2}} - \frac{1}{x} + 4m - 2020\). Tổng tất cả các giá trị nguyên của tham số m để hai đồ thị hàm số cắt nhau tại một điểm duy nhất bằng:
A.506
B.1011
C.2020
D.1010
Đồ thị của hàm số y = f(x) đối xứng với đồ thị của hàm số \[y = {a^x}(a > 0,a \ne 1)\;\] qua điểm M(1;1). Giá trị của hàm số y = f(x) tại \[x = 2 + lo{g_a}\frac{1}{{2020\;}}\] bằng:
A.−2020
B.−2018
C.2020
D.2019
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị \[y = {\log _a}x,y = {\log _b}x\] và trục hoành lần lượt tại A,B và H phân biệt ta đều có 3HA=4HB (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
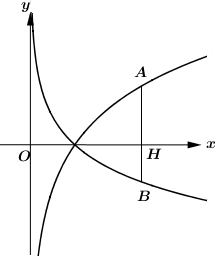
A.\[{a^3}{b^4} = 1\]
B. \[3a = 4b\]
C. \[4a = 3b\]
D. \[{a^4}{b^3} = 1\]
Cho hàm số \[f\left( x \right) = \ln \left( {{e^x} + m} \right)\]có \[f'\left( { - \ln 2} \right) = \frac{3}{2}\]. Mệnh đề nào dưới đây đúng?
A.\[m \in \left( { - 2;\,\,0} \right).\]
B. \[m \in \left( { - 5;\, - 2} \right).\]
C. \[m \in \left( {0;\,\,1} \right).\]
D. \[m \in \left( {1;\,\,3} \right).\]
Xét các số thực a, b thỏa mãn a>b>1. Tìm giá trị nhỏ nhất Pmin của biểu thức \[P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\frac{a}{b}\].
A.\[{P_{\min }} = 19\]
B. \[{P_{\min }} = 13\]
C. \[{P_{\min }} = 14\]
D. \[{P_{\min }} = 15\]

