Quiz

Tổng hợp đề thi thptqg môn Toán cực hay mới nhất (Đề số 03)

Admin50 câu hỏiToánTốt nghiệp THPT

50 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Đường cong trong hình dưới đây là một phần đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D

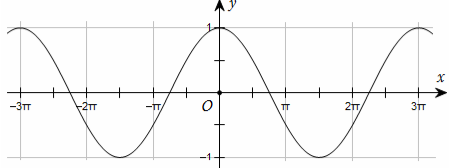
Hỏi hàm số đó là hàm số nào?

A. $y = \cos \frac{3 x}{2}$

B. $y = \cos \frac{3 x}{2}$

C. $y = \sin \frac{3 x}{2}$

D. $y = \cos \frac{2 x}{3}$

2. Nhiều lựa chọn

Đặt $a = \log_{7} 11, b = \log_{2} 7 .$ Biểu diễn $\log_{\sqrt{7}} \frac{121}{8} = ma + \frac{n}{b} .$ Tính tổng $m^{2} + n^{2} .$

A. -5

B. 52

C. 5

D. $\frac{13}{4}$

3. Nhiều lựa chọn

Với giá trị nào của m thì hàm số $y = x^{3} + {mx}^{2} + 1$ đồng biến trong khoảng $(1; 2)$ ?

A. $m > o$

B. $m \geq - \frac{3}{2}$

C. $- \frac{3}{2} < m \leq 0$

D. $m \geq 0$

4. Nhiều lựa chọn

Trong các khẳng định sau, khẳng định nào là đúng?

A. $a \subset (P), b \subset (Q)$ và a chéo b thì (P)//(Q)

B. $a / / b, b \subset (P), a ⊄ (P), a \subset (Q), (P) \cap (Q) = c$ thì a//c

C. a//b và $b \subset (P)$ thì a//(P)

D. $(Q) \cap (P) = a, (R) \cap (P) = b$ và a//b thì (R)//(Q)

5. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , $AD = 2 a, AB = BC = a, SA$ vuông góc với đáy, SB tạo với đáy một góc $30^{o} .$ Tính tỉ số thể tích $\frac{V_{SABD}}{V_{SBCD}} ?$

A. $\frac{1}{2}$

B. 3

C. $\frac{1}{4}$

D. 2

6. Nhiều lựa chọn

Tiếp tuyến của đồ thị hàm số $y = x^{3} + 3 x^{2}$ tại tiếp điểm $M (- 1; 2)$ có hệ số góc k bằng

A. k = 2

B. k = -2

C. k = -1

D. k = -3

7. Nhiều lựa chọn

Trong không gian Oxyz cho các đường thẳng

$d_{1} : \{\begin{cases} x + 2 y - 3 z + 1 = 0 \\ 2 x - 3 y + z + 1 = 0 \end{cases}$ và $d_{2} : \{\begin{cases} x = 2 + at \\ y = - 1 + 2 t \\ z = 3 - 3 t \end{cases}$

Trong đó t là tham số, a là một số thực cho trước. Xác định a để tồn tại mặt phẳng (Q) chứa $d_{1}$ và vuông góc với $d_{2}$

A. a = 1

B. a = -1

C. a = 2

D. a = -2

8. Nhiều lựa chọn

Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức $- 2, 4 i, x + 2 i$ . Với giá trị nào của x thì A, B, M thẳng hàng.

A. x = 1

B. x = -3

C. x = 3

D. x = -1

9. Nhiều lựa chọn

Để kiểm tra chất lượng sản phần từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phân kiểm nghiệm chọn ngẫu nhiên 3 hộp sữa để phân tích mẫu. Tính xác suất để 3 hộp sữa được chọn có cả 3 loại.

A. $\frac{15}{22}$

B. $\frac{7}{22}$

C. $\frac{3}{11}$

D. $\frac{8}{11}$

10. Nhiều lựa chọn

Hàm số $f (x) = e^{x} cosx$ có một nguyên hàm $F (x)$ là kết quả nào sau đây, biết nguyên hàm này bằng $\frac{3}{2}$ khi x=0

A. $F (x) = \frac{cosx . e^{x} - sinx . e^{x}}{2} + 1$

B. $F (x) = \frac{sinx . e^{x} - cosx . e^{x}}{2} + 2$

C. $F (x) = \frac{cosx . e^{x} + sinx . e^{x}}{2} + 1$

D. $F (x) = \frac{{cosxe}^{x}}{2} + 1$

11. Nhiều lựa chọn

Cho đa giác đều 20 đỉnh nội tiếp đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật.

A. $\frac{6}{323}$

B. $\frac{23}{4845}$

C. $\frac{3}{323}$

D. $\frac{37}{4845}$

12. Nhiều lựa chọn

Hình vẽ sau đây giống đồ thị của hàm số nào nhất?

A. $\frac{x + 1}{2 x - 2}$

B. $\frac{x + 2}{2 x - 2}$

C. $\frac{x - 1}{2 x + 2}$

D. $\frac{x - 3}{2 x - 2}$

13. Nhiều lựa chọn

Giới hạn $\lim_{x \to 1} \frac{x^{2} - mx + m - 1}{x - 1}$ (m là tham số) có giá trị bằng

A. 2 - m

B. 0

C. m - 2

D. $+ \infty$

14. Nhiều lựa chọn

Cho hai đường thẳng $d : x + y - 1 = 0$ và $d^{'} : x + y - 5 = 0$ . Phép tịnh tiến theo vecto $\vec{u}$ biến đường thẳng d thành d’. Khi đó, độ dài bé nhất của là bao nhiêu?

A. 5

B. $\sqrt{2}$

C. $2 \sqrt{2}$

D. $4 \sqrt{2}$

15. Nhiều lựa chọn

Cho hàm số phù hợp với bảng biến thiên sau. Phát biểu nào sau đây là đúng?

A. Giá trị cực tiểu của hàm số là 0

B. Giá trị cực đại của hàm số là −1

C. Hàm số đạt cực đại tại x = -1 và đạt cực tiểu tại x = 0

D. Hàm số đạt cực tiểu tại x = -1 và đạt cực đại tại x = 2

16. Nhiều lựa chọn

Cho $0 < a < 1, 0 < x < y .$ . Phát biểu nào sau đây là đúng?

A. $lga > 0$

B. $lna > 0$

C. $\log_{a} x > \log_{a} y$

D. $a^{x} < a^{y}$

17. Nhiều lựa chọn

Tìm giá trị của m để đồ thị hàm số $y = x^{4} - 2 x^{2} - 3 + m$ cắt trục hoành tại 4 nghiệm phân biệt.

A. $m \leq 4$

B. $3 < m < 4$

C. $m < 4$

D. $m > 3$

18. Nhiều lựa chọn

Trong mặt phẳng Oxy, cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc $45^{o}$ ?

A. $(0; \sqrt{2})$

B. $(- 1; 1)$

C. $(\sqrt{2}; 0)$

D. $(1; 0)$

19. Nhiều lựa chọn

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x^{3} + 2 x + 1$ (C) , tiếp tuyến của đồ thị tại x = 1 và đường thẳng x = 0, thuộc góc phần tư thứ (I),(IV) là

A. $\frac{5}{2}$

B. $\frac{3}{4}$

C. 4

D. 3

20. Nhiều lựa chọn

Tỉ số thể tích hình cầu và thể tích hình trụ cùng ngoại tiếp một hình lập phương bằng

A. $\sqrt{2}$

B. $2 \sqrt{3}$

C. $2 \sqrt{2}$

D. $\sqrt{3}$

21. Nhiều lựa chọn

Cho hình phẳng (H) giới hạn bởi các đường y=x,y=−x,x=3. Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành.

A. $\frac{\sqrt{3} a}{2}$

B. $π$

C. $2 \sqrt{3}$

D. $\sqrt{3}$

22. Nhiều lựa chọn

Tìm giao tuyến của hai mặt phẳng $(P) : x - 2 y + z - 3 = 0$ và $(Q) : x - 3 y + z - 4 = 0$ .

A. $d : \{\begin{cases} x = - t \\ y = - 1 \\ z = 1 - t \end{cases}$

B. $d : \{\begin{cases} x = t \\ y = - 1 \\ z = 1 - t \end{cases}$

C. $d : \{\begin{cases} x = t \\ y = - t \\ z = 1 - t \end{cases}$

D. $d : \{\begin{cases} x = t \\ y = - 1 + t \\ z = 1 - t \end{cases}$

23. Nhiều lựa chọn

Cho hàm số $f (x) = \{\begin{cases} 2 x - 2 khix \neq 3 \\ m - 1 khix = 3 \end{cases}$ (m là tham số). Hàm số đã cho liên tục tại x = 3 khi m bằng

A. m = 3

B. m = 4

C. m = 1

D. m = 5

24. Nhiều lựa chọn

Cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 4 x - 2 y + 2 z + 5 = 0$ và mặt phẳng $(P) : 3 x - 2 y + 6 z + m = 0$ . (S) và (P) giao nhau khi

A. m > 3 hoặc m < 2

B. m > 9 hoặc m < -5

C. $- 5 \leq m \leq 9$

D. $2 \leq m \leq 3$

25. Nhiều lựa chọn

Với giá trị nào của m thì điểm $A (1; 2)$ và hai điểm cực trị của đồ thị hàm số $y = x^{3} + 3 x^{2} + m$ thẳng hàng?

A. $m = \frac{1}{2}$

B. m = 4

C. m = 3

D. m = 2

26. Nhiều lựa chọn

Tìm véctơ $\vec{u}$ biết rằng véctơ $\vec{u}$ vuông góc với véctơ $\vec{a} = (1; - 2; 1)$ và thỏa mãn $\vec{u} . \vec{b} = - 1; \vec{u} . \vec{c} = - 5, \vec{b} = (4; - 5; 2), \vec{c} = (8; 4; - 5) .$

A. $\vec{u} = (5; 3; 1)$

B. $\vec{u} = (3; - 5; 1)$

C. $\vec{u} = (1; 3; 5)$

D. $\vec{u} = (- 1; 3; 5)$

27. Nhiều lựa chọn

Số nghiệm của phương trình $\tan (x + \frac{π}{6}) = \sqrt{3}$ thuộc đoạn $[\frac{π}{2}; 2 π]$ là

A. 4

B. 1

C. 3

D. 2

28. Nhiều lựa chọn

Số phức z thỏa mãn $(2 + 3 i) \bar{z} + (1 - i) z = 3 + 5 i$ . Tìm môđun của số phức z.

A. 11

B. $\frac{\sqrt{610}}{11}$

C. $\frac{23}{11}$

D. 9

29. Nhiều lựa chọn

Cho hình lăng trụ đứng có đáy là một hình vuông cạnh a và chiều cao bằng 4a. Tính diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó.

A. $12 {πa}^{2}$

B. $18 {πa}^{2}$

C. $9 {πa}^{2}$

D. $15 {πa}^{2}$

30. Nhiều lựa chọn

Phần thực của số phức $w = 1 + (1 + i) + {(1 + i)}^{2} + {(1 + i)}^{3} + . .. + {(1 + i)}^{1999}$ bằng

A. 0

B. $\frac{1}{\sqrt{2}}$

C. 1

D. $\frac{1}{2}$

31. Nhiều lựa chọn

Tính giá trị biểu thức $A = \frac{2 I + 1}{I + 3}$ biết $I =_{- 2}^{1} |x| dx$

A. $\frac{12}{11}$

B. $\frac{5}{2}$

C. $\frac{2}{5}$

D. $\frac{11}{12}$

32. Nhiều lựa chọn

Cho hàm số $y = x - e^{x} .$ Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $(0; + \infty)$

B. Hàm số có tập xác định là $(0; + \infty)$

C. Hàm số đạt cực đại tại x = 0

D. Hàm số không có cực trị

33. Nhiều lựa chọn

Cho cấp số nhân $(u_{n})$ có $u_{1} = - \frac{1}{2}$ và $u_{2} = 1$ . Tính $u_{8}$

A. 64

B. $\frac{1}{256}$

C. 256

D. -128

34. Nhiều lựa chọn

Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = x \sqrt{4 - x^{2}}$

A. -2

B. 4

C. 2

D. 0

35. Nhiều lựa chọn

Cho hai hàm số $y = a^{x}$ và $y = \log_{a} x$ với $(0 < a \neq 1)$ . Khẳng định sai là?

A. Đồ thị hàm số $y = \log_{a} x$ nằm phía trên trục Ox

B. Hàm số $y = a^{x}$ có tập xác định là tập số thực

C. Đồ thị hàm số $y = a^{x}$ nhận Ox làm đường tiệm cận ngang

D. Hàm số $y = a^{x}$ và $y = \log_{a} x$ đồng biến trên mỗi tập xác định tương ứng của nó khi a>1

36. Nhiều lựa chọn

Giá trị lớn nhất của hàm số $y = 2 sinx - 3 \cos 2 x + 1$ là

A. 12

B. 2

C. 6

D. 4

37. Nhiều lựa chọn

Tìm tập xác định của hàm số $y = \sqrt{\log_{x} {(x - 2)}^{2} - 1}$

A. $x \geq 4$

B. $x \neq 2$

C. $x \geq 0, x \neq 1$

D. $x > 2$

38. Nhiều lựa chọn

Một đàn ong có số lượng là $5 {.10}^{3}$ thành viên. Biết mỗi năm, số lượng thành viên của đàn ong tăng 2% so với năm trước. Hỏi sau 5 năm, số lượng thành viên của đàn ong là bao nhiêu?

A. ${5.10}^{3} .1, 12^{5}$ (thành viên).

B. $5 {.10}^{3} (1 + 0, 02^{5})$ (thành viên).

C. $5 {.10}^{3} + 1, 02^{5}$ (thành viên).

D. $5 {.10}^{3} . 1, 02^{5}$ (thành viên).

39. Nhiều lựa chọn

Tìm giá trị của a để $I = \int_{0}^{a} \frac{5 x + 7}{x^{2} + 3 x + 2} dx = 3 \ln 2 + 2 \ln 3 .$

A. $a = \frac{3}{2}$

B. a = 1

C. a = 3

D. a = 2

40. Nhiều lựa chọn

Cho hàm số $f (x) = \frac{x^{2} - 4 x}{7 x}$ với $x \neq 0$ . Phải bổ sung thêm giá trị $f (0)$ bằng bao nhiêu thì hàm số $f (x)$ liên tục trên R?

A. 0

B. $\frac{4}{7}$

C. $\frac{1}{7}$

D. $- \frac{4}{7}$

41. Nhiều lựa chọn

Cho $x > 0, x \neq 1$ thỏa mãn biểu thức $\frac{1}{\log_{2} x} + \frac{1}{\log_{3} x} + . .. + \frac{1}{\log_{1993} x} = M$ . Chọn khẳng định đúng trong các khẳng định sau

A. $x = \sqrt[1993]{\frac{1993!}{M}}$

B. $x = \frac{1993!}{M}$

C. $x = 1993^{M}$

D. $x = \sqrt[M]{1993!}$

42. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại $A, AB = 2 a, AC = 2 a$ . Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy (ABC) một góc $45^{o} .$ Khoảng cách từ A đến mặt phẳng (SBC) là

A. $\frac{\sqrt{3} a}{\sqrt{11}}$

B. $\frac{2 \sqrt{5} a}{\sqrt{11}}$

C. $\frac{\sqrt{5} a}{\sqrt{11}}$

D. $\frac{2 \sqrt{3} a}{\sqrt{11}}$

43. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x}{x + 1}$ . Tìm điểm M thuộc đồ thị (C), biết tiếp tuyến của (C) tại M cắt Ox và Oy tại hai điểm A, B và ΔOAB có diện tích bằng 14.

A. $M (2; \frac{4}{3})$

B. $M (\frac{1}{2}; \frac{2}{3})$

C. $M (3; \frac{3}{2})$

D. $M (1; 1)$ hoặc $M (- \frac{1}{2}; - 2)$

44. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, $AB = a, AD = 2 a .$ . Khoảng cách giữa hai đường thẳng AB và SD bằng $a \sqrt{3}$ . Thể tích khối chóp S.ABCD bằng

A. $\frac{2 \sqrt{3} a^{3}}{3}$

B. $\frac{\sqrt{3} a^{3}}{6}$

C. $\frac{\sqrt{3} a^{3}}{3}$

D. $\frac{\sqrt{3} a^{3}}{2}$

45. Nhiều lựa chọn

Viết phương trình đường thẳng Δ qua $A (0; 1; 0)$ và cắt cả hai đường thẳng $d_{1} : \frac{x - 2}{1} = \frac{y - 1}{2} = \frac{z}{1}; d_{2} \{\begin{cases} x + z - 3 = 0 \\ y - z = 0 \end{cases}$ .

A. $\{\begin{cases} x + y - 2 z - 1 = 0 \\ x + 3 y - 2 z - 3 = 0 \end{cases}$

B. $\{\begin{cases} 3 x + y - 2 z - 1 = 0 \\ x + 3 y - 2 z - 3 = 0 \end{cases}$

C. $\{\begin{cases} y - 2 z - 1 = 0 \\ x + 3 y - 3 = 0 \end{cases}$

D. $\{\begin{cases} y - 2 z - 1 = 0 \\ x + 3 y - 2 z - 3 = 0 \end{cases}$

46. Nhiều lựa chọn

Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết $SO = h; OB = R; OH = x (0 < x < h) .$ Tìm thể tích lớn nhất của hình trụ.

A. $\frac{2 {πR}^{2} h}{27}$

B. $\frac{2 {πR}^{2} h}{9}$

C. $\frac{4 {πR}^{2} h}{9}$

D. $\frac{4 {πR}^{2} h}{27}$

47. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A, $\hat{ABC} = 30^{0}$ tam giác SBC đều cạnh a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABC). Tính khoảng cách từ A đến (SBC).

A. $\frac{a}{\sqrt{6}}$

B. $\frac{3 a \sqrt{14}}{7}$

C. $\frac{a \sqrt{2}}{3}$

D. $\frac{2 a}{\sqrt{7}}$

48. Nhiều lựa chọn

Từ các chữ số $A = \{0; 1; 2; 3; 4; 5\}$ có thể lập được bao nhiêu số tự nhiên có 5 chữ số và số đó chia hết cho 3?

A. 1980

B. 2160

C. 1120

D. 1080

49. Nhiều lựa chọn

Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B, $AB = BC = 2 a$ , $\hat{SAB} = \hat{SCB} = 90^{o}$ . Và khoảng cách từ A đến mặt phẳng (SBC) bằng $a \sqrt{2}$ . Tính diện tích mặt cầu ngoại tiếp S.ABC theo a.