10 bài tập Một số bài toán hàm hợp liên quan đến giá trị lớn nhất và giá trị nhỏ nhất của hàm số của hàm có lời giải

Giá trị lớn nhất của hàm số f(x) = |x³ – 3x² – 1| trên đoạn [−1; 3] là

Cho hàm số y = f(x) có đạo hàm của hàm số như sau: f'(x) = (x – 3)(x + 3)(x – 1)². Gọi g(x) = f(−2x + 3). Khi đó giá trị nhỏ nhất của hàm số g(x) trên đoạn [0; 3] là:

Cho hàm số y = f(x) liên tục trên tập ℝ và có bảng biến thiên như sau

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x² – 2x) trên đoạn \(\left[ { - \frac{3}{2};\frac{7}{2}} \right]\). Tìm khẳng định sai trong các khẳng định sau.

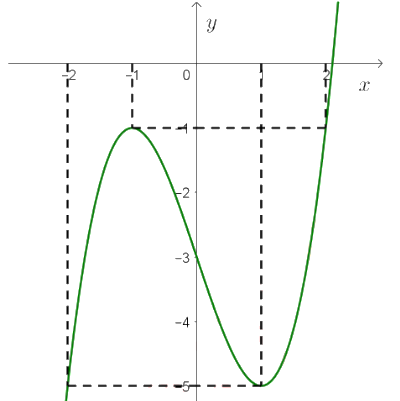
Cho hàm số y = f(x) có đồ thị như hình vẽ. Gọi M, m là các giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \sqrt {2x - {x^2}} \). Giá trị của 2M – m bằng

Cho hàm số y = f(x) liên tục trên ℝ có đồ thị như hình vẽ

Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(1 − cosx) trên \(\left[ {0;\frac{{3\pi }}{2}} \right]\). Giá trị của M + m bằng

Cho hàm số y = f(x) có đồ thị trên đoạn [−2; 4] như hình vẽ bên. Tìm \[\mathop {\max }\limits_{\left[ { - 2;{\rm{ 4}}} \right]} \left| {f\left( x \right)} \right|\].

Cho đồ thị hàm số y = f(x) như hình vẽ.

Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = |f(x)| trên đoạn [−1; 1] lần lượt là M, m. Tính giá trị của biểu thức T = 673M – 2019m.

Cho hàm số y = f(x) có đồ thị hàm số như hình vẽ

Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = |f(2x – 1)| trên đoạn \(\left[ {0\,;\,\frac{1}{2}} \right]\). Tính giá trị M – m.

Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau

Giá trị nhỏ nhất của hàm số y = f(|x|) trên đoạn [−2; 4] bằng