13 CÂU HỎI
Cho ba vecto . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng?
A. Một trong ba vecto đó bằng
B. Có hai trong ba vecto đó cùng phương
C. Có một vecto không cùng hướng với hai vecto còn lại.
D. Có hai trong ba vecto đó cùng hướng
Các đường thẳng cùng vuông góc với một đường thẳng thì.
A. Thuộc một mặt phẳng
B. vuông góc với nhau
C.song song với một mặt phẳng
D. song song với nhau.
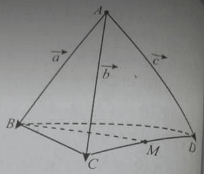
Cho tứ diện ABCD và đặt . Gọi M là trung điểm của CD.
Vecto bằng:
A.
B.
C.
D.
Cho tứ diện ABCD và đặt . Gọi M là trung điểm của CD.
Vecto bằng:
A.
B.
C.
D.
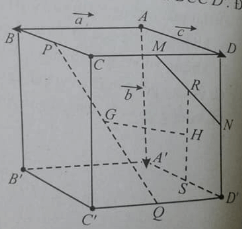
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt .
Vecto bằng:
A.
B.
C.
D.
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt .
Đường thẳng GG’ song song với mặt phẳng (AA’B’B) vì:
A. Vecto cùng phương với vecto
B. Vecto cùng phương với vecto
C. Vecto đồng phẳng với hai vecto
D. Vecto đồng phẳng với hai vecto .
Mệnh đề nào sau đây sai?
A. Qua một điểm O cho trước có duy nhất một mặt phẳng (P) vuông góc với một đường thẳng a cho trước.
B. Qua một điểm O cho trước có duy nhất một đường thẳng a vuông góc với một mặt phẳng (P) cho trước.
C. Có duy nhất một mặt phẳng (P) đi qua một điểm O cho trước, vuông góc với một đường thẳng a cho trước.
D. Có duy nhất một đường thẳng a vuông góc với một mặt phẳng (P) cho trước, biết rẳng (P) đi qua điểm O cho trước.
Mặt phẳng trung trực của đoạn thẳng AB
A. Luôn luôn vuông góc với AB tại một điểm bất kì trên AB.
B. Luôn cách đều hai đầu mút A và B.
C. Luôn vuông góc với AB tại trung điểm của AB.
D. Luôn luôn song song với AB.
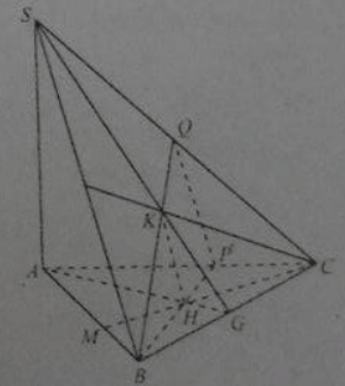
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Đường thẳng BH vuông góc với đường thẳng:
A. AG
B. SC
C. CM
D. SG
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Mặt phẳng (BKH) vuông góc với đường thẳng:
A. SC
B. AC
C. AH
D. AB
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Mặt phẳng (BKH) vuông góc với mặt phẳng:
A. (ABC)
B. (SAB)
C. (SAG)
D. (SAC)
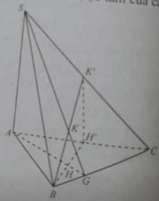
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC:
Mặt phẳng (BKH) vuông góc với đường thẳng:
A. SC
B. AC
C. AH
D. AB
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC:
Đường thẳng HK vuông góc với mặt phẳng:
A. (ABC)
B. (BK’H’)
C. (ASG)
D. (SBC)
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
