16 CÂU HỎI
Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình có nghiệm duy nhất?
A. 4
B. 3
C. 1
D. 2
Giả sử phương trình (với m là tham số) có hai nghiệm . Tìm giá trị nhỏ nhất của biểu thức
A.
B.
C.
D.
Gọi S là tập hợp các giá trị của tham số m sao cho parabol (P): cắt Ox tại hai điểm phân biệt A, B thỏa mãn OA = 3OB. Tính tổng T các phần tử của S.
A. T = 3.
B. T = −15.
C. .
D. T = −9.
Phương trình có bao nhiêu nghiệm?
A. 2
B. 3
C. 1
D. 0
Tập nghiệm của phương trình là:
A.
B.
C.
D.
Tìm m để phương trình có ba nghiệm phân biệt.
A. m = ±1.
B. m = 1.
C. m = −1.
D. m = 0.
Phương trình có bao nhiêu nghiệm nguyên?
A. 4
B. 1
C. 2
D. 0
Cho hàm số có đồ thị (P), và đường thẳng (d) có phương trình . Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho đạt giá trị nhỏ nhất
A.
B.
C.
D.
Số nghiệm của phương trình là:
A. 3
B. 1
C. 4
D. 2
Tập hợp tất cả các giá trị của tham số m để phương trình có nghiệm là:
A.
B.
C.
D.
Cho phương trình . Tìm m để phương trình có một nghiệm duy nhất?
A.
B.
C.
D. m=2
Tổng bình phương các nghiệm của phương trình là:
A. 5
B. 13
C. 10
D. 25
Tìm tất cả các giá trị của m để phương trình có nghiệm
A. m ∈ (−∞; 5].
B. m ∈ [−4; −3].
C. m ∈ [−4; 5].
D. m ∈ [3; +∞)
Cho hàm số f(x) xác định trên R có đồ thị như hình vẽ.
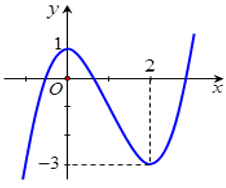
Phương trình có bao nhiêu nghiệm?
A. 1
B. 3
C. 2
D. 4
Tổng các bình phương các nghiệm của phương trình là:
A. 17
B. 4
C. 16
D. 8
Tìm phương trình đường thẳng . Biết đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 6?
A.
B.
C.
D.


