Quiz

194 câu Chuyên đề Toán 12 Bài 4: Tiệm cận có đáp án

Admin190 câu hỏiToánLớp 12

190 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có $\lim_{x \to - \infty} f (x) = - 3$ và $\lim_{x \to + \infty} f (x) = 3$ . Mệnh đề nào dưới đây đúng?

A. Đồ thị hàm số đã cho có hai tiệm cận ngang là x=3 và y=-3

B. Đồ thị hàm số đã cho có hai tiệm cận ngang là x=3 và y=-3

C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang

D. Đồ thị hàm số đã cho không có tiệm cận ngang

2. Nhiều lựa chọn

Cho hàm số $y = f (x)$ xác định và có đạo hàm trên $ℝ \ \{- 2; 1\}$ và có bảng biến thiên như sau:

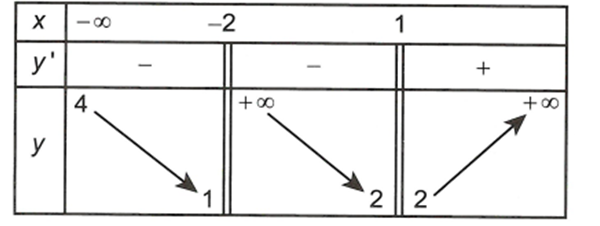
Cho hàm số y=f(x) xác định và có đạo hàm trên R/{-2,1} và có bảng biến thiên như sau: Phương trình đường tiệm cận đứng của đồ (ảnh 1)

Phương trình đường tiệm cận đứng của đồ thị hàm số đã cho là

A. $x = - 2$ và x=1

B. không có tiệm cận đứng

C. x=-2

D. x=1

3. Nhiều lựa chọn

Cho hàm số y = f(x) có đồ thị như hình vẽ dưới.

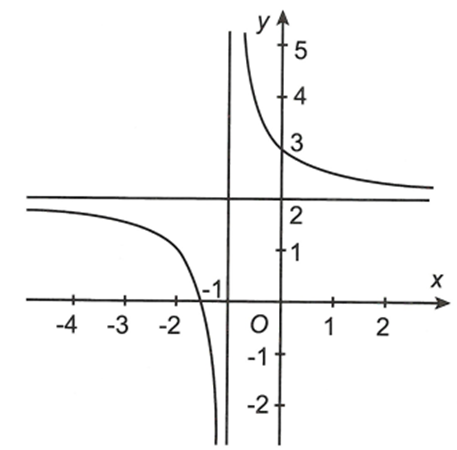
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới. Phương trình các đường tiệm cận của đồ thị hàm số y=f(x) là (ảnh 1)

Phương trình các đường tiệm cận của đồ thị hàm số $y = f (x)$ là

A. x=1 và y=-2

B. x=1 và y=2

C. x=-1 và y=2

D.x=1 và y=-2

4. Nhiều lựa chọn

Phương trình các đường tiệm cận của đồ thị hàm số $y = \frac{x + 1}{x - 2}$ là

A. $x = - 2 y = 1$

B. $x = 1; y = 2$

C. $x = 2; y = 1$

D. $x = 2; y = - 1$

5. Nhiều lựa chọn

Đồ thị hàm số nào sau đây nhận đường thẳng x=2 là tiệm cận đứng?

A. $y = \frac{2 x}{x - 2}$

B. $y = 2$

C. $y = \frac{2 x}{x + 2}$

D. $y = x - 2 - \frac{2}{x}$

6. Nhiều lựa chọn

Tọa độ tâm đối xứng của đồ thị hàm số $y = \frac{3 x + 1}{x - 1}$ là

A. $(- 1; 3)$

B. $(- 1; 1)$

C. $(3; 1)$

D. $(1; 3)$

7. Nhiều lựa chọn

Các đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 1}{x - 1}$ tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

A. 2 (đvdt)

B. 3 (đvdt)

C. 1 (đvdt)

D. 4 (đvdt)

8. Nhiều lựa chọn

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{|x - \sqrt{2}|}{x - 2}$ là

A. 4

B. 3

C. 2

D. 1

9. Nhiều lựa chọn

Đồ thị của hàm số $y = \frac{x + 1}{x^{2} + 2 x - 3}$ có bao nhiêu đường tiệm cận?

A. 3

B. 2

C. 1

D. 0

10. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{|x| + 1}{|x| - 1}$ có bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 4

D. 3

11. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{(x^{2} - 3 x + 2) \sin x}{x^{3} - 4 x}$ có bao nhiêu đường tiệm cận đứng?

A. 1

B. 2

C. 3

D. 4

12. Nhiều lựa chọn

Số đường tiệm cận của đồ thị hàm số $y = \frac{\sqrt{x + 9} - 3}{x^{2} + x}$ là

A. 3

B. 4

C. 2

D. 1

13. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{\sqrt{16 - x^{2}}}{x (x - 16)}$ có bao nhiêu đường tiệm cận?

A. 4

B. 2

C. 0

D. 1

14. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{\sqrt{x + 1}}{|x| - 1}$ có bao nhiêu đường tiệm cận?

A. 0

B. 1

C. 2

D. 3

15. Nhiều lựa chọn

Phương trình các đường tiệm cận ngang của đồ thị hàm số $y = \frac{2 x + 1 + \sqrt{x^{2} + 1}}{x - 3}$ là

A. $y = 1$

B. y=3 và y=1

C. $y = 2$

D. $y = 3$

16. Nhiều lựa chọn

Biết các đường tiệm cận của đường cong $(C) : y = \frac{6 x + 1 - \sqrt{x^{2} - 2}}{x - 5}$ và trục tung cắt nhau tạo thành một đa giác $(H)$ . Mệnh đề nào dưới đây đúng?

A. $(H)$ là một hình chữ nhật có diện tích bằng 8

B. $(H)$ là một hình vuông có diện tích bằng 4

C. $(H)$ là một hình vuông có diện tích bằng 25

D. $(H)$ là một hình chữ nhật có diện tích bằng 10

17. Nhiều lựa chọn

Cho hàm số $y = x + \sqrt{x^{2} + 2 x + 3}$ . Khi đó, đồ thị hàm số

A. có tiệm cận đứng và không có tiệm cận ngang

B. có tiệm cận ngang và không có tiệm cận đứng

C. có tiệm cận đứng và tiệm cận ngang

D. không có cả tiệm cận đứng và tiệm cận ngang

18. Nhiều lựa chọn

Phương trình các đường tiệm cận ngang của đồ thị hàm số $y = \frac{|x|}{\sqrt{x^{2} - 1}}$ là

A. y=1 và $y = - 1$

B. $y = 1$

C. $y = - 1$

D. Không có tiệm cận ngang

19. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có $\lim_{x \to + \infty} f (x) = 2$ và $\lim_{x \to - \infty} f (x) = - 2$ . Mệnh đề nào sau đây đúng?

A. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng y=2 và y=-2

B. Đồ thị hàm số đã cho không có đường tiệm cận ngang

C. Đồ thị hàm số đã cho có đúng một đường tiệm cận ngang

D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng x=2 và x=-2

20. Nhiều lựa chọn

Hàm số $y = f (x)$ xác định với mọi $x \neq \pm 1$ , có $\lim_{x \to 1^{+}} f (x) = + \infty, \lim_{x \to {(- 1)}^{-}} = - \infty, \lim_{x \to + \infty} f (x) = + \infty$ , $\lim_{x \to - \infty} f (x) = - \infty$ . Mệnh đề nào dưới đây đúng?

A. Đồ thị hàm số có hai tiệm cận đứng

B. Đồ thị hàm số có một tiệm cận đứng

C. Đồ thị hàm số không có tiệm cận đứng

D. Đồ thị hàm số có hai tiệm cận ngang

21. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có $\lim_{x \to 3^{+}} f (x) = - \infty$ và $\lim_{x \to 3^{-}} f (x) = 2$ . Mệnh đề nào sau đây đúng?

A. Đường thẳng $y = 2$ là tiệm cận ngang của đồ thị hàm số $y = f (x)$

B. Đồ thị hàm số $y = f (x)$ không có tiệm cận đứng

C. Đường thẳng x=3 là tiệm cận đứng của đồ thị hàm số $y = f (x)$

D. Đường thẳng x=3 không phải là tiệm cận của đồ thị hàm số $y = f (x)$

22. Nhiều lựa chọn

Cho hàm số $f (x)$ xác định và liên tục trên $ℝ \ \{- 1\}$ có bảng biến thiên như sau

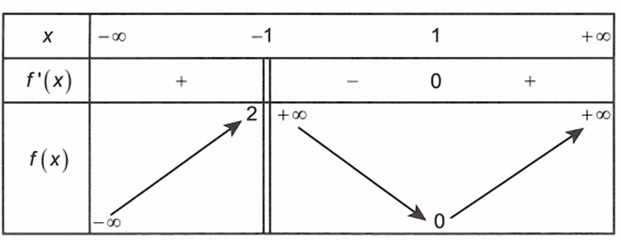
$Cho hàm số f(x) xác định và liên tục trên R\{-1} có bảng biến thiên như sau Mệnh đề nào sau đây sai? (ảnh 1)$

Mệnh đề nào sau đây sai?

A. Đồ thị hàm số không có tiệm cận ngang

B. Hàm số không có đạo hàm tại x=-1

C. Hàm số đã cho đạt cực tiểu tại x=1

D. Đồ thị hàm số không có tiệm cận đứng

23. Nhiều lựa chọn

Cho hàm số $y = f (x)$ xác định trên $ℝ \ \{1\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình dưới

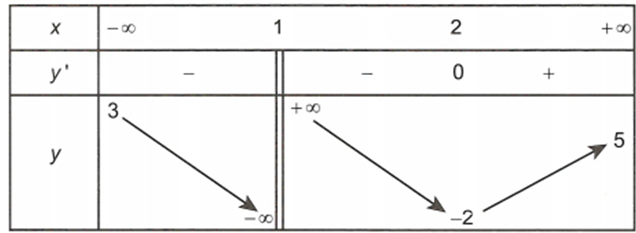
$Cho hàm số y= f(x) xác định trên R\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình dưới (ảnh 1)$

Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

A. 3

B. 1

C. 2

D. 4

24. Nhiều lựa chọn

Cho hàm số y=f(x) xác định trên R\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau

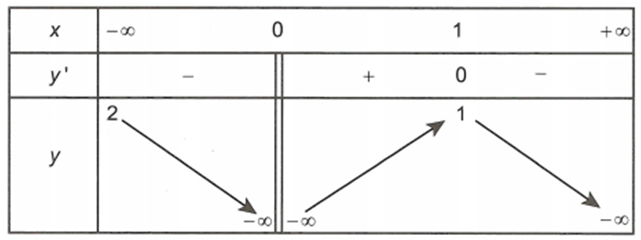
$Cho hàm số y=f(x) xác định trên R\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau (ảnh 1)$

Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 3

D. 4

25. Nhiều lựa chọn

Cho hàm số y= f(x) có bảng biến thiên như sau

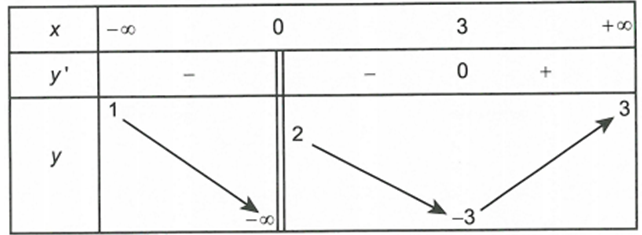
Cho hàm số y=f(x) có bảng biến thiên như sau Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là (ảnh 1)

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

A. 3

B. 4

C. 1

D. 2

26. Nhiều lựa chọn

Cho hàm số y= f(x) có bảng biến thiên như hình vẽ. Đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

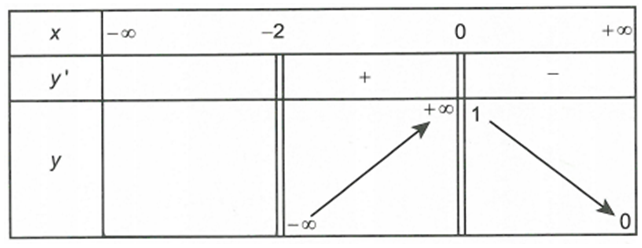
Cho hàm số y= f(x) có bảng biến thiên như hình vẽ. Đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận? (ảnh 1)

A. 4

B. 1

C. 3

D. 2

27. Nhiều lựa chọn

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=f(x) có bảng biến thiên như sau

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y= f(x) có bảng biến thiên như sau (ảnh 1)

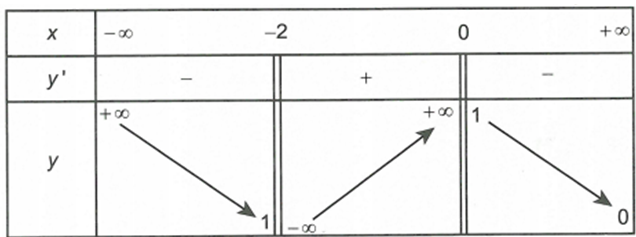
A. 0

B. 1

C. 3

D. 2

28. Nhiều lựa chọn

Phương trình đường tiệm cận ngang của đồ thị hàm số $y = \frac{x + 2}{1 - x}$ là

A. $y = - 1$

B. $x = - 1$

C. x= 1

D. y=1

29. Nhiều lựa chọn

Đồ thị của hàm số $y = \frac{x + 2}{3 - x}$ có bao nhiêu đường tiệm cận?

A. 2

B. 3

C. 1

D. 4

30. Nhiều lựa chọn

Đường tiệm cận đứng của đồ thị hàm số $y = \frac{2 x - 1}{x + 1}$ là

A. y= -2

B. x=1

C. y=2

D. x=-1

31. Nhiều lựa chọn

Hàm số nào dưới đây có đồ thị nhận đường thẳng x=2 là đường tiệm cận?

A. $y = \frac{5 x}{2 - x}$

B. $y = x - 2 + \frac{1}{x + 1}$

C. $y = \frac{2}{x + 2}$

D. $y = \frac{1}{x + 1}$

32. Nhiều lựa chọn

Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 - 5 x}{2 x + 3}$ là

A. $(- \frac{3}{5}; \frac{5}{2})$

B. $(- \frac{5}{2}; - \frac{3}{2})$

C. $(- \frac{3}{2}; - \frac{5}{2})$

D. $(\frac{3}{2}; - \frac{5}{2})$

33. Nhiều lựa chọn

Tổng khoảng cách từ điểm $M (1; - 2)$ đến hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 1}{x - 1}$ là

A. 4

B. 2

C. 1

D. 3

34. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{2 x}{x^{2} + 1}$ có bao nhiêu đường tiệm cận ngang?

A. 2

B. 1

C. 3

D. 0

35. Nhiều lựa chọn

Đường thẳng y=-1 là tiệm cận ngang của đồ thị hàm số nào sau đây?

A. $y = \frac{1 + x}{1 - x}$

B. $y = \frac{2 x^{2} + 3 x + 2}{x - 2}$

C. $y = \frac{2 x - 2}{x + 2}$

D. $y = \frac{1 + x^{2}}{1 + x}$

36. Nhiều lựa chọn

Phương trình đường tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} - 2 x + 3}{2 x - 4}$ là

A. $x = 2$

B. $x = - 1$

C. $y = 1$

D. $x = 1$

37. Nhiều lựa chọn

Phương trình đường tiệm cận ngang của đồ thị hàm số $y = \frac{2 x}{x + 1} - \frac{3 x}{2 x - 1}$ là

A. $y = 2$

B. $x = \frac{1}{2}$

C. $y = \frac{1}{2}$

D. $y = - \frac{3}{2}$

38. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{x^{2} - 5 x + 6}{x^{2} - 3 x + 2}$ có bao nhiêu đường tiệm cận đứng?

A. 1

B. 3

C. 0

D. 2

39. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x^{2} - 3 x + 2}{x^{2} - 2 x - 3}$ . Mệnh đề nào sau đây sai?

A. Đồ thị hàm số có ba đường tiệm cận

B. Đồ thị hàm số có hai tiệm cận đứng là $x = - 1$ và $x = 3$

C. Đồ thị hàm số có tiệm cận ngang là $y = \frac{1}{2}$

D. Đồ thị hàm số có tiệm cận ngang là y=2

40. Nhiều lựa chọn

Số đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 2017}{|x| + 1}$ là

A. 1

B. 2

C. 3

D. 4

41. Nhiều lựa chọn

Số đường tiệm cận đứng và tiệm cận ngang của đồ thị tham số $y = \frac{x^{3} + x}{x^{2} - x - 2}$ là

A. 2

B. 1

C. 3

D. 0

42. Nhiều lựa chọn

Số đường tiệm cận của đồ thị hàm số $y = \frac{1 - \sqrt{4 - x^{2}}}{x^{2} - 2 x - 3}$ là

A. 0

B. 2

C. 3

D. 1

43. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{\sqrt{x^{2} - 2 x - 3}}{x - 2}$ có bao nhiêu đường tiệm cận?

A. 3

B. 1

C. 2

D. 4

44. Nhiều lựa chọn

Phương trình các đường tiệm cận của đồ thị hàm số $y = \frac{\sqrt{4 - x} + 1}{\sqrt{x} - 1}$ là

A. $x = 1; y = 2$

B. $x = 1$

C. $x = 0; y = - 1$

D. $x = 1; y = - 1$

45. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{x + 1}{\sqrt{4 - x^{2}}}$ có bao nhiêu đường tiệm cận?

A. 2

B. 0

C. 1

D. 4

46. Nhiều lựa chọn

Đồ thị hàm số nào sau đây có đúng hai đường tiệm cận ngang?

A. $y = \frac{\sqrt{x^{2} - x}}{|x| + 2}$

B. $y = \frac{\sqrt{x + 2}}{|x| - 2}$

C. $y = \frac{|x| - 2}{x + 1}$

D. $y = \frac{\sqrt{4 - x^{2}}}{x + 1}$

47. Nhiều lựa chọn

Đồ thị hàm số nào sau đây có đúng hai đường tiệm cận ngang?

A. $y = \frac{\sqrt{x^{2} - x}}{|x| + 2}$

B. $y = \frac{\sqrt{x + 2}}{|x| - 2}$

C. $y = \frac{|x| - 2}{x + 1}$

D. $y = \frac{\sqrt{4 - x^{2}}}{x + 1}$

48. Nhiều lựa chọn

Gọi n, d lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số $y = \frac{\sqrt{1 - x}}{(x - 1) \sqrt{x}}$ . Giá trị của n, d là

A. $n = 1; d = 2$

B. $n = 0; d = 1$

C. $n = 0; d = 2$

D. $n = d = 1$

49. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{\sqrt{3 x^{2} + 2}}{\sqrt{2 x + 1} - x}$ có tất cả bao nhiêu đường tiệm cận?

A. 1

B. 4

C. 3

D. 2

50. Nhiều lựa chọn

Phương trình các đường tiệm cận ngang của đồ thị hàm số $y = \frac{2 x - 1}{\sqrt{4 x^{2} + 3}}$ là

A. $y = 1$

B. $y = 1$ và $y = - 1$

C. $y = 2$

D. $y = 2$ và $y = - 2$

51. Nhiều lựa chọn

Đồ thị hàm số $y = 2 x - 1 + \sqrt{4 x^{2} - 4}$ có bao nhiêu đường tiệm cận ngang?

A. 1

B. 0

C. 3

D. 2

52. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{2 x}{\sqrt{x^{2} + 1} - x}$ có bao nhiêu đường tiệm cận?

A. 2

B. 1

C. 3

D. 4

53. Nhiều lựa chọn

Đồ thị hàm số $y = \sqrt{4 x^{2} + 4 x + 3} - \sqrt{4 x^{2} + 1}$ có bao nhiêu đường tiệm cận ngang?

A. 2

B. 0

C. 1

D. 3

54. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{\sqrt{x^{2} - 4}}{2 x^{2} - 5 x + 2}$ có bao nhiêu đường tiệm cận?

A. 2

B. 1

C. 3

D. 4

55. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{2 x + 4}{x - m}$ có tiệm cận đứng là

A. $m < - 2$

B. $m \neq - 2$

C. $m > - 2$

D. $m = - 2$

56. Nhiều lựa chọn

Giá trị của tham số thực m để đồ thị hàm số $y = \frac{(2 m - 1) x + 1}{x - m}$ có đường tiệm cận ngang $y = 3$ là

A. m=1

B. m=0

C. m=2

D. m=3

57. Nhiều lựa chọn

Tập hợp các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x - 1}{m x - 1}$ có tiệm cận đứng là

A. R

B. $ℝ \ \{0\}$

C. $ℝ \ \{1\}$

D. $ℝ \ \{0; 1\}$

58. Nhiều lựa chọn

Tập hợp các giá trị của tham số m để đồ thị hàm số $y = \frac{x - 3}{m x - 1}$ không có tiệm cận đứng là

A. R

B. $\{0; \frac{1}{3}\}$

C. $\{\frac{1}{3}\}$

D. $\{0\}$

59. Nhiều lựa chọn

Cho hàm số $y = \frac{a x + b}{x + 1}$ . Biết đồ thị hàm số đã cho đi qua điềm $A (0; - 1)$ và có đường tiệm cận ngang là $y = 1$ . Giá trị $a + b$ bằng

A. 1

B. 0

C. 3

D. 2

60. Nhiều lựa chọn

Giá trị thực của tham số m để đường tiệm cận đứng của đồ thị hàm số $y = \frac{x + 1}{2 x + m}$ đi qua điểm $A (1; 2)$ là

A. m=4

B. m=-2

C. m=-4

D. m=2

61. Nhiều lựa chọn

Cho hàm số $y = \frac{m x + 1}{x - 2 m}$ với tham số $m \neq 2$ . Giao điểm của hai đường tiệm cận của đồ thị hàm số thuộc đường thẳng nào dưới đây?

A. $x + 2 y = 0$

B. $2 x + y = 0$

C. $x - 2 y = 0$

D. $y = 2 x$

62. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{4 x - 5}{x - m}$ có tiệm cận đứng nằm bên phải trục tung là

A. $m > 0$ và $m \neq 2$

B. $m > 0$

C. $m > 0$ và $m \neq \frac{3}{4}$

D. $m < 0$

63. Nhiều lựa chọn

Cho hàm số $y = \frac{2}{x^{2} - 2 m x + 3 m - 1}$ . Giá trị của tham số thực m để đồ thị hàm số đã cho nhận đường thẳng $x = 2$ là tiệm cận đứng là

A. m=3

B. m=2

C. $m \neq 3$

D. $m \neq 2$

64. Nhiều lựa chọn

Giá trị thực của tham số m để đồ thị hàm số $y = \frac{2 x^{2} - 3 x + m}{x - m}$ không có tiệm cận đứng là

A. $m = 0$

B. $m = 1$

C. $m = 0; m = 1$

D. $m = 0; m = - 1$

65. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{m x^{2} - 2 x + 1}{2 x + 1}$ có tiệm cận đứng là

A. $m = 8$

B. $m = 0$

C. $m \neq 4$

D. $m \neq - 8$

66. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{x - 1}{x^{2} - 2 m x + n + 6}$ (m, n là tham số) nhận đường thẳng x=1 là tiệm cận đứng, giá trị của m+n bằng

A. 6

B. 10

C. -4

D. -7

67. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{(2 m - n) x^{2} + m x + 1}{x^{2} + m x + n - 6}$ nhận trục hoành và trục tung làm hai tiệm cận. Giá trị $m + n$ bằng

A. 8

B. 9

C. 6

D. -6

68. Nhiều lựa chọn

Cho hàm số $y = \frac{a x^{2} + x - 1}{4 x^{2} + b x + 9}$ có đồ thị (a, b là các số thực dương và $a b = 4$ ). Biết rằng (C) có tiệm cận ngang $y = c$ và có đúng một tiệm cận đứng.

Giá trị của tổng $T = 3 a + b - 24 c$ bằng

A. 8

B. 9

C. 6

D. 11

69. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{(2 m + 1) x^{2} + 3}{\sqrt{x^{4} + 1}}$ có đường tiệm cận ngang đi qua điểm $A (1; - 3)$ là

A. $m = 0$

B. $m = \pm 1$

C. $m = - 2$

D. $m = 2$

70. Nhiều lựa chọn

Biết đồ thị hàm số $y = 2 x + \sqrt{a x^{2} + b x + 4}$ có tiệm cận ngang $y = - 1$

Giá trị $2 a - b^{3}$ bằng

A. 56

B. -56

C. 72

D. -72

71. Nhiều lựa chọn

Có bao nhiêu giá trị của tham số m để đồ thị hàm số $y = \frac{m x + \sqrt{x^{2} - 2 x + 3}}{2 x - 1}$ có một đường tiệm cận ngang là $y = 2$ ?

A. 0

B. vô số

C. 1

D. 2

72. Nhiều lựa chọn

Biết rằng đồ thị hàm số $y = \frac{a x + 1}{x - b}$ có tiệm cận đứng là $x = 2$ , tiệm cận ngang là y=-3. Khi đó a+b bằng

A. -1

B. 2

C. 1

D. -2

73. Nhiều lựa chọn

Các giá trị thực của tham số m để đồ thị hàm số $y = \frac{(m + 1) x - 2 m + 1}{x - 1}$ không có tiệm cận đứng là

A. $m = 2$

B. $m = \frac{1}{2}$

C. m=1

D. m=-1

74. Nhiều lựa chọn

Cho hàm số $y = \frac{a x + 1}{b x - 2}$ . Giá trị của tham số a và b để đồ thị hàm số nhận đường thẳng $x = 1$ làm tiệm cận đứng và đường $y = \frac{1}{2}$ thẳng làm tiệm cận ngang là

A. $a = 2; b = 2$

B. $a = 2; b = - 2$

C. $a = 1; b = 2$

D. $a = - 1; b = - 2$

75. Nhiều lựa chọn

Giá trị của tham số m để đường tiệm cận đứng của đồ thị hàm số $y = \frac{m x - 1}{2 x + m}$ đi qua điểm $A (1; 2)$ là

A. $m = - 2$

B. $m = - 4$

C. $m = - 5$

D. $m = 2$

76. Nhiều lựa chọn

Có bao nhiêu giá trị của tham số m để đồ thị hàm số $y = \frac{x + m}{m x + 1}$ không có đường tiệm cận đứng?

A. 0

B. 1

C. 3

D. 2

77. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{a x + 1}{b x - 2}$ có đường tiệm cận đứng là x=2 và đường tiệm cận ngang là y=3, giá trị của a+b bằng

A. 4

B. 0

C. 1

D. 5

78. Nhiều lựa chọn

Tất cả các giá trị của tham số m để đồ thị hàm số $y = \frac{m x + 2}{x - 1}$ có tiệm cận đứng là

A. $m \neq 2$

B. $m \neq - 2$

C. $m \leq - 2$

D. $m < 2$

79. Nhiều lựa chọn

Cho hàm số $y = \frac{2 m x + 1}{x - m}$ với tham số $m \neq 0$ . Giao điểm của hai đường tiệm cận của đồ thị hàm số đã cho thuộc đường thẳng nào dưới đây?

A. $2 x + y = 0$

B. $y = 2 x$

C. $x - 2 y = 0$

D. $x + 2 y = 0$

80. Nhiều lựa chọn

Giá trị của tham số m để đường tiệm cận đứng của đồ thị hàm số $y = \frac{x + 3}{x + m - 1}$ đi qua điểm $A (5; 2)$ là

A. $m = - 1$

B. $m = 6$

C. $m = 4$

D. $m = - 4$

81. Nhiều lựa chọn

Cho hàm số $y = \frac{m x + 1}{x + 3 n + 1}$ . Biết đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Khi đó tổng $m + n$ bằng

A. 0

B. $- \frac{1}{3}$

C. $\frac{1}{3}$

D. $\frac{2}{3}$

82. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đường tiệm cận ngang của đồ thị hàm số $y = \frac{m x + 5}{x + 1}$ đi qua điểm $M (10; - 3)$ là

A. $m = 5$

B. $m = - 3$

C. $m = 3$

D. $m = - \frac{1}{2}$

83. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{- 3 x + 1}{x - 2 m}$ có hai đường tiệm cận và hai đường tiệm cận đó cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 1 là

A. $m = \pm \frac{1}{6}$

B. $m = \pm \frac{1}{3}$

C. $m = - \frac{1}{6}$

D. $m = \frac{1}{6}$

84. Nhiều lựa chọn

Biết đồ thị của hàm số $y = \frac{(n - 3) x + n - 2019}{x + m + 3}$ (m, n là tham số) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tổng $m - 2 n$ bằng

A. 0

B. -3

C. -9

D. 6

85. Nhiều lựa chọn

Đồ thị hàm số $f (x) = \frac{a x - 1}{x + b}$ đi qua điểm $M (1; 2)$ và có đường tiệm cận đứng là đường thẳng $x = - 2$ . Giá trị $f (- 1)$ bằng

A. 2

B. -8

C. $- \frac{1}{2}$

D. 6

86. Nhiều lựa chọn

Có bao nhiêu giá trị thực của tham số m để hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x - m - 1}{x - m^{2}}$ cắt nhau tại điểm thuộc đường thẳng $y = x + 1$ ?

A. 1

B. -1

C. 0

D. 2

87. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{x + 2}{3 x + 9}$ có đường tiệm cận đứng là $x = a$ và đường tiệm cận ngang là $y = b$ . Giá trị nguyên của tham số m nhỏ nhất thỏa mãn $m \geq a + b$ là

A. $m = - 1$

B. $m = - 2$

C. $m = 0$

D. $m = - 3$

88. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{a x + 1}{x + d}$ đi qua $M (2; 5)$ và có đường tiệm cận đứng là đường thẳng x=1 thì tổng $a + d$ bằng

A. 1

B. 8

C. 7

D. 3

89. Nhiều lựa chọn

Biết đồ thị của hàm số $y = \frac{(a - 2 b) x^{2} + b x + 1}{x^{2} + x - b}$ có tiệm cận đứng là đường thẳng $x = 1$ và tiệm cận ngang là đường thẳng $y = 0$ . Giá trị $a + 2 b$ bằng

A. 7

B. 8

C. 10

D. 9

90. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{(4 a - b) x^{2} + a x + 1}{x^{2} + a x + b - 12}$ nhận trục hoành và trục tung làm hai tiệm cận thì giá trị $a + b$ bằng

A. 10

B. 15

C. 2

D. -10

91. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{x^{3} + a x^{2} + b x + c}{{(x - 2)}^{2}}$ không có tiệm cận đứng. Giá trị $b + c$ bằng

A. 9

B. 4

C. 1

D. 7

92. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{x^{4} + a x^{2} + b}{{(x - 1)}^{2}}$ không có tiệm cận đứng. Giá trị ab bằng

A. 2

B. -1

C. -2

D. 1

93. Nhiều lựa chọn

Biết rằng đồ thị hàm số $y = \frac{\sqrt{3 x + 1} + a x + b}{{(x - 1)}^{2}}$ không có tiệm cận đứng. Giá trị ab bằng

A. -2

B. 2

C. $\frac{15}{16}$

D. $\frac{- 15}{16}$

94. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{\sqrt{5 x + 1} + a x + b}{{(x - 3)}^{2}}$ không có tiệm cận đứng. Giá trị $a + 2 b$ bằng

A. $- \frac{11}{4}$

B. $\frac{29}{8}$

C. $- \frac{39}{8}$

D. $- \frac{27}{8}$

95. Nhiều lựa chọn

Với các số thực dương a, b để đồ thị hàm số $y = \frac{\sqrt{a + b x} - \sqrt{2}}{x - 2}$ có đúng một đường tiệm cận. Giá trị lớn nhất của biểu thức $\log_{a + 1} \frac{b}{2}$ bằng

A. $\frac{1}{2}$

B. 2

C. -1

D. -2

96. Nhiều lựa chọn

Cho hàm số y= f(x) liên tục trên R và có đồ thị như hình vẽ.

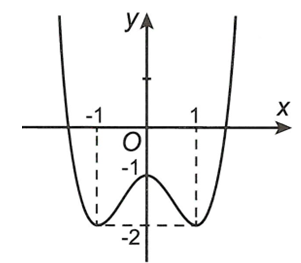
Cho hàm số y= f(x) liên tục trên R và có đồ thị như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số y= 1/ f(x)+1 là (ảnh 1)

Số đường tiệm cận đứng của đồ thị hàm số $y = \frac{1}{f (x) + 1}$ là

A. 2

B. 3

C. 4

D. 1

97. Nhiều lựa chọn

Cho hàm số y= f(x) liên tục trên R và có bảng biến thiên như hình vẽ dưới đây.

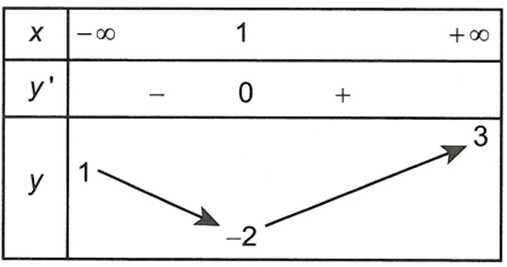
Cho hàm số y= f(x) liên tục trên R và có bảng biến thiên như hình vẽ dưới đây. Tổng số đường tiệm cận của hàm số y= 1/ f(x)+1 là (ảnh 1)

Tổng số đường tiệm cận của hàm số $y = \frac{1}{f (x) + 1}$ là

A. 2

B. 3

C. 1

D. 4

98. Nhiều lựa chọn

Cho hàm số $y = f (x)$ xác định, liên tục trên R và có bảng biến thiên như hình vẽ bên dưới.

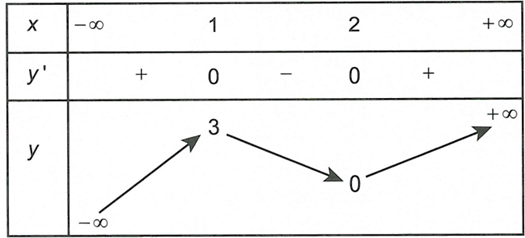
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ bên dưới. Tổng số tiệm cận ngang và tiệm cận đứng (ảnh 1)

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = \frac{1}{f (x^{3} + x) + 3}$ là

A. 2

B. 4

C. 3

D. 1

99. Nhiều lựa chọn

Cho hàm số bậc ba $f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ)$ có đồ thị như hình vẽ dưới đây.

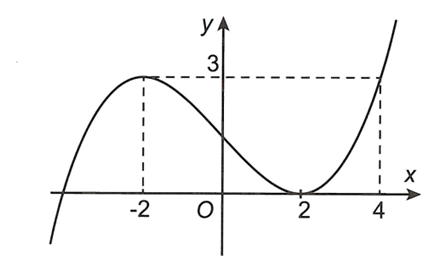
Cho hàm số bậc ba f(x)= ax^3+bx^2+ cx+d ( a,b,c,d thuộc R) có đồ thị như hình vẽ dưới đây. Đồ thị hàm số g(x)= 1/ f(4-x^2)-3 (ảnh 1)

Đồ thị hàm số $g (x) = \frac{1}{f (4 - x^{2}) - 3}$ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

A. 2

B. 3

C. 4

D. 5

100. Nhiều lựa chọn

Cho hàm số bậc ba $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ.

Cho hàm số bậc ba f(x)= ã^3+bx^2+cx+d có đồ thị như hình vẽ. Đồ thị hàm số g(x)= (x^2-3x+2) căn 2x+1/ ( x^4-5x^2+4)f(x) (ảnh 1)

Đồ thị hàm số $g (x) = \frac{(x^{2} - 3 x + 2) \sqrt{2 x + 1}}{(x^{4} - 5 x^{2} + 4) f (x)}$ có bao nhiêu đường tiệm cận đứng?

A. 2

B. 6

C. 4

D. 3

101. Nhiều lựa chọn

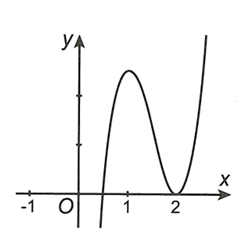
Cho hàm số bậc ba $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ.

Cho hàm số bậc ba f(x)= ax^3+bx^2+cx+d có đồ thị như hình vẽ. Đồ thị hàm số g(x)= ( x^2-3x+2) căn x-1/ x [f^2(x)-f(x)] có bao nhiêu (ảnh 1)

Đồ thị hàm số $g (x) = \frac{(x^{2} - 3 x + 2) \sqrt{x - 1}}{x [f^{2} (x) - f (x)]}$ có bao nhiêu đường tiệm cận đứng?

A. 4

B. 6

C. 3

D. 5

102. Nhiều lựa chọn

Cho hàm số bậc ba $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ dưới đây.

Cho hàm số bậc ba f(x)= ax^3+bx^2+cx+d có đồ thị như hình vẽ dưới đây. Đặt g(x)= x^2-x/ f^2(x)-2f(x) . (ảnh 1)

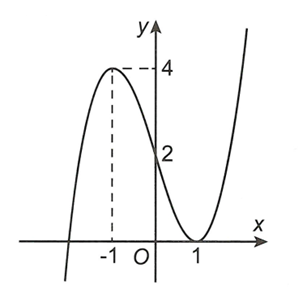
Đặt $g (x) = \frac{x^{2} - x}{f^{2} (x) - 2 f (x)}$ . Đồ thị hàm số $y = g (x)$ có bao nhiêu đường tiệm cận đứng?

A. 4

B. 2

C. 5

D. 3

103. Nhiều lựa chọn

Cho $f (x)$ là hàm đa thức bậc 6 có bảng biến thiên như sau

Cho f(x) là hàm đa thức bậc 6 có bảng biến thiên như sau Đồ thị hàm số g(x)= (x-3)(x^2-4x+3)/ f'(x)[f(x)-2] có bao nhiêu đường tiệm cận đứng? (ảnh 1)

Đồ thị hàm số $g (x) = \frac{(x - 3) (x^{2} - 4 x + 3)}{f^{'} (x) [f (x) - 2]}$ có bao nhiêu đường tiệm cận đứng?

A. 3

B. 2

C. 4

D. 1

104. Nhiều lựa chọn

Cho hàm số $y = f (x)$ là hàm đa thức bậc 6 thỏa mãn $3 f (1) - 2 < 0$ và $3 f (a) - a^{3} + 3 a > 0, \forall a > 2$ . Đồ thị hàm số $y = f^{'} (x)$ như hình vẽ.

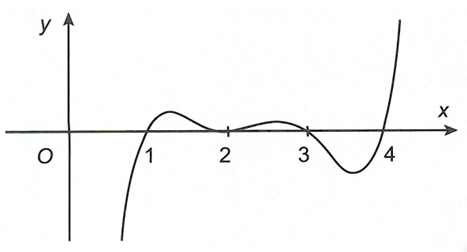
Cho hàm số y=f(x) là hàm đa thức bậc 6 thỏa mãn 3f(1)-2<0 và 3f(a)-a^3+3a>0, với a >2 . Đồ thị hàm số y=f(x) như hình vẽ. (ảnh 1)

Số đường tiệm cận đứng của đồ thị hàm số $g (x) = \frac{x + 1}{3 f (x + 2) - x^{3} + 3 x}$ là

A. 0

B. 2

C. 1

D. 3

105. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên $ℝ \ \{1\}$ và có bảng biến thiên như sau

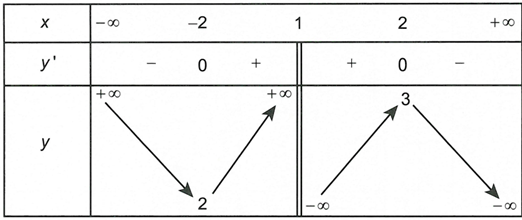
$Cho hàm số y=f(x) liên tục trên R\{1} và có bảng biến thiên như sau Đồ thị hàm số y= 1/ 2f(x)-5 có bao nhiêu đường tiệm cận đứng? (ảnh 1)$

Đồ thị hàm số $y = \frac{1}{2 f (x) - 5}$ có bao nhiêu đường tiệm cận đứng?

A. 0

B. 4

C. 2

D. 1

106. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên từng khoảng xác định và có bảng biến thiên sau

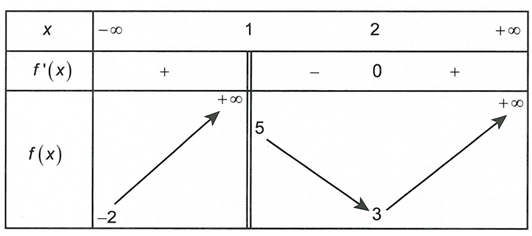
Cho hàm số y=f(x) liên tục trên từng khoảng xác định và có bảng biến thiên sau Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số y=1/ f(x)-5 là (ảnh 1)

Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số $y = \frac{1}{f (x) - 5}$ là

A. 2

B. 3

C. 4

D. 5

107. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có bảng biến thiên như sau

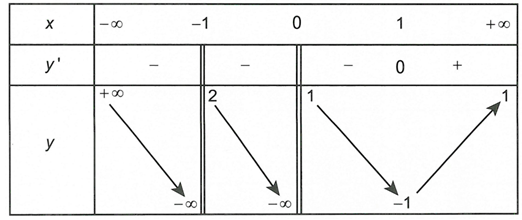
Cho hàm số y=f(x) có bảng biến thiên như sau Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y= 2/ 3f(x)-2 là (ảnh 1)

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{2}{3 f (x) - 2}$ là

A. 3

B. 4

C. 5

D. 6

108. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên $ℝ \ \{1\}$ và có bảng biến thiên như sau

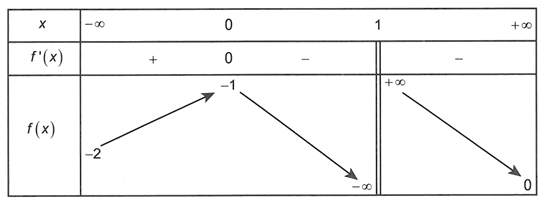
$Cho hàm số y=f(x) liên tục trên R\{1} và có bảng biến thiên như sau Đồ thị hàm số y=1/ 2f(x)+3 có bao nhiêu đường tiệm cận đứng? (ảnh 1)$

Đồ thị hàm số $y = \frac{1}{2 f (x) + 3}$ có bao nhiêu đường tiệm cận đứng?

A. 3

B. 0

C. 2

D. 1

109. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có bảng biến thiên như sau

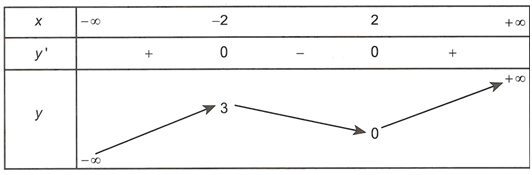
Cho hàm số y=f(x) có bảng biến thiên như sau Đồ thị hàm số y= 1/ f(3-x)-2 có bao nhiêu tiệm cận đứng? (ảnh 1)

Đồ thị hàm số $y = \frac{1}{f (3 - x) - 2}$ có bao nhiêu tiệm cận đứng?

A. 3

B. 1

C. 0

D. 2

110. Nhiều lựa chọn

Cho hàm số bậc ba $y = f (x)$ có đồ thị như hình vẽ bên. Số tiệm cận đứng của đồ thị hàm số $y = \frac{2020}{f (x) - 1}$ là

A. 1

B. 2

C. 3

D. 4

111. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có bảng biến thiên như hình vẽ sau

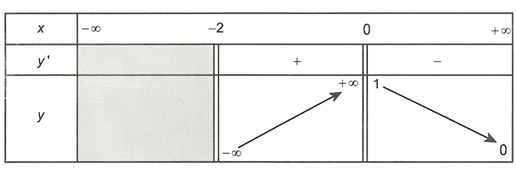
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau Đồ thị của hàm số y= 1/ 2f(x)-1 có tất cả bao nhiêu đường tiệm cận ngang? (ảnh 1)

Đồ thị của hàm số $y = \frac{1}{2 f (x) - 1}$ có tất cả bao nhiêu đường tiệm cận ngang?

A. 1

B. 2

C. 3

D. 0

112. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có bảng biến thiên như hình vẽ

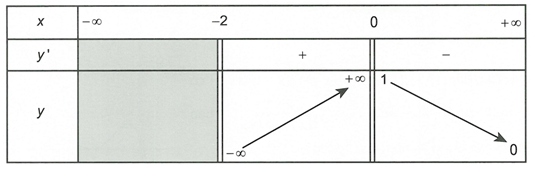
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ Đồ thị của hàm số y= 1/ 2f(x)-1 có bao nhiêu đường tiệm cận? (ảnh 1)

Đồ thị của hàm số $y = \frac{1}{2 f (x) - 1}$ có bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 3

D. 0

113. Nhiều lựa chọn

Cho hàm số $y = f (x)$ xác định trên $ℝ \ \{- 1; 1\}$ , có đạo hàm trên $ℝ \ \{- 1; 1\}$ và có bảng biến thiên như sau

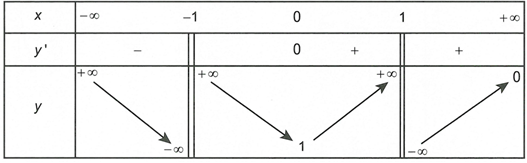
$Cho hàm số y=f(x) xác định trên R\{-1,1} , có đạo hàm trên R\{-1,1} và có bảng biến thiên như sau (ảnh 1)$

Đồ thị hàm số $y = \frac{1}{f (x) - 1}$ có bao nhiêu tiệm cận đứng và tiệm cận ngang?

A. 2

B. 3

C. 4

D. 5

114. Nhiều lựa chọn

Cho hàm số $y = f (x)$ xác định, liên tục trên và có bảng biến thiên như sau

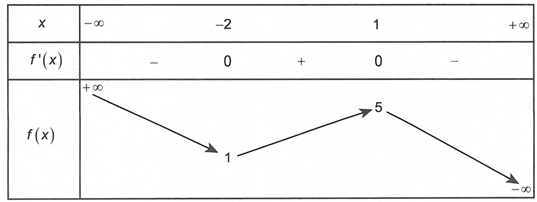
Cho hàm số y=f(x) xác định, liên tục trên và có bảng biến thiên như sau Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y=1/f(x^3+2x)-5 là (ảnh 1)

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = \frac{1}{f (x^{3} + 2 x) - 5}$ là

A. 2

B. 4

C. 3

D. 1

115. Nhiều lựa chọn

Cho hàm số bậc bốn $y = f (x)$ có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số $y = \frac{(x^{2} - 4) . (x^{2} + 2 x)}{{[f (x)]}^{2} + 2 f (x) - 3}$

là

Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số y= (x^2-4)(x^2+2x)/ [f(x)]^2+2f(x)-3 là (ảnh 1)

A. 2

B. 5

C. 3

D. 4

116. Nhiều lựa chọn

Cho hàm số $f (x) = (x + 3) {(x + 1)}^{2} (x - 1) (x - 3)$ có đồ thị như hình vẽ. Đồ thị hàm số $g (x) = \frac{\sqrt{x - 1}}{f^{2} (x) - 9 f (x)}$ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

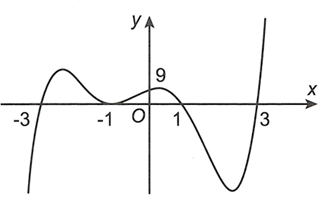
Cho hàm số f(x)=(x+3)( x+1)^2(x-10(x-3) có đồ thị như hình vẽ. Đồ thị hàm số g(x)= căn x-1/ f^2(x)-9f(x) có bao nhiêu đường tiệm (ảnh 1)

A. 8

B. 3

C. 4

D. 9

117. Nhiều lựa chọn

Cho hàm bậc ba $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ bên. Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{x^{4} - 4 x^{2} + 3}{(x - 1) (f^{2} (x) - 2 f (x))}$ là

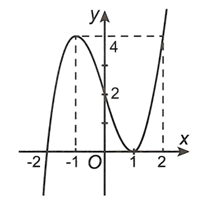
Cho hàm bậc ba f(x)=ax^3+bx^2+cx+d có đồ thị như hình vẽ bên. Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=x^4-4x^2+3 (ảnh 1)

A. 4

B. 5

C. 2

D. 3

118. Nhiều lựa chọn

Cho hàm số bậc ba $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ bên. Đồ thị hàm số $g (x) = \frac{(x^{2} - 2 x) \sqrt{1 - x}}{(x - 3) [f^{2} (x) + 3 f (x)]}$ có bao nhiêu đường tiệm cận đứng?

Cho hàm số bậc ba f(x)=ax^3+bx^2+cx+d có đồ thị như hình vẽ bên. Đồ thị hàm số g(x)=(x^2-2x) căn 1-x/ ( x-3)[f^2(x)+3f(x)] có bao nhiêu (ảnh 1)

A. 5

B. 4

C. 6

D. 3

119. Nhiều lựa chọn

Cho hàm số bậc ba $y = f (x)$ có đồ thị hàm số như hình vẽ bên dưới. Đồ thị hàm số $g (x) = \frac{\sqrt{x}}{(x + 1) [f^{2} (x) - f (x)]}$ có bao nhiêu tiệm cận đứng?

A. 3

B. 0

C. 1

D. 2

120. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có bảng biến thiên như hình vẽ sau

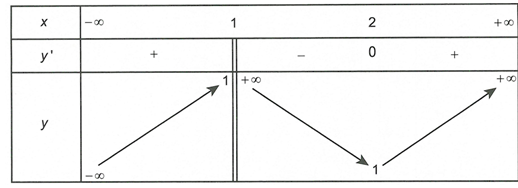
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y=1/ e^f (ảnh 1)

Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số $y = \frac{1}{e^{f^{2} (x)} - 3}$ là

A. 4

B. 3

C. 5

D. 2

121. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có bảng biến thiên như hình vẽ sau

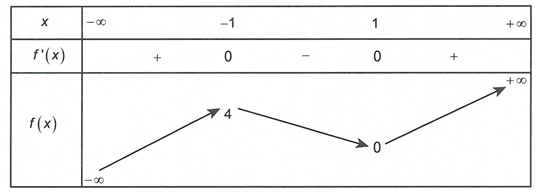
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau Hỏi đồ thị hàm số y=x^4-1/ f^2(x)-4f(4) có bao nhiêu tiệm cận đứng? (ảnh 1)

Hỏi đồ thị hàm số $y = \frac{x^{4} - 1}{f^{2} (x) - 4 f (x)}$ có bao nhiêu tiệm cận đứng?

A. 5

B. 2

C. 3

D. 4

122. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có đạo hàm liên tục trên $ℝ \ \{1\}$ và có bảng biến thiên như hình vẽ sau

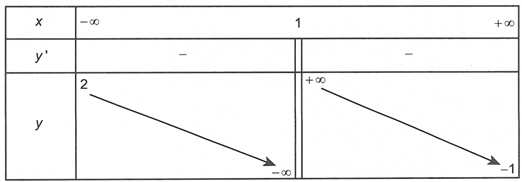
$Cho hàm số y=f(x) có đạo hàm liên tục trên R\{1} và có bảng biến thiên như hình vẽ sau (ảnh 1)$

Đặt $g (x) = \frac{2 f (x) - 3}{f (x) - 1}$ . Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = g (x)$ là

A. 4

B. 5

C. 6

D. 3

123. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên R và có bảng biến thiên như sau

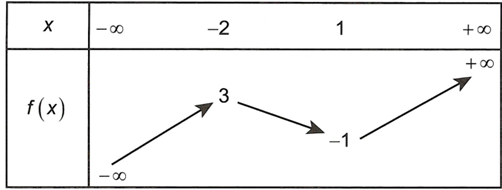
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau Đồ thị hàm số y=1/ e^2f(x)-1-1 có bao nhiêu tiệm cận ngang (ảnh 1)

Đồ thị hàm số $y = \frac{1}{e^{2 f (x) - 1} - 1}$ có bao nhiêu tiệm cận ngang và tiệm cận đứng?

A. 2

B. 3

C. 4

D. 5

124. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên R và có bảng biến thiên như sau

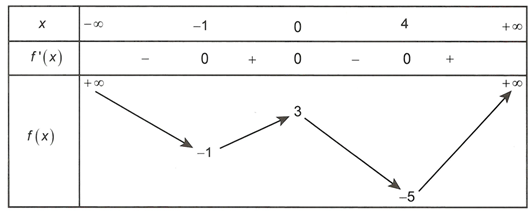
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau Đồ thị hàm số y=f^2(x)+2f(x)+1/ f^2(x)-9 có tổng số tất cả các (ảnh 1)

Đồ thị hàm số $y = \frac{f^{2} (x) + 2 f (x) + 1}{f^{2} (x) - 9}$ có tổng số tất cả các đường tiệm cận đứng và đường tiệm cận ngang là

A. 4

B. 5

C. 6

D. 7

125. Nhiều lựa chọn

Gọi S là tập các giá trị nguyên dương của tham số m để đồ thị hàm số $y = \frac{x + 2}{x^{2} + 2 x + m^{2} - 3 m}$ có ba tiệm cận. Tổng các giá trị của tập S bằng

A. 6

B. 19

C. 3

D. 15

126. Nhiều lựa chọn

Tổng tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x^{2} + m}{x^{2} - 3 x + 2}$ có đúng hai đường tiệm cận là

A. -5

B. 4

C. -1

D. 5

127. Nhiều lựa chọn

Tính tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{x^{2} - 3 x + 2}{x^{2} - m x - m + 5}$ không có đường tiệm cận đứng

A. -12

B. 12

C. 15

D. -15

128. Nhiều lựa chọn

Tập hợp các giá trị thực của tham số m để đồ thị hàm số $y = \frac{2 x - 1}{(m x^{2} - 2 x + 1) (4 x^{2} + 4 m x + 1)}$ có đúng một đường tiệm cận là

A. $\{- 1; 0\}$

B. $\{0\}$

C. $(- \infty; - 1) \cup \{0\}$

D. $(- \infty; - 1) \cup (1; + \infty)$

129. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{\sqrt{m x^{2} - 4}}{x - 3}$ có đúng ba tiệm cận là

A. $m \geq \frac{4}{9}$

B. $m > 0$

C. $0 < m < \frac{4}{9}$

D. $\forall m \in ℝ$

130. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x + 1 - \sqrt{x^{2} + 3 x}}{x^{2} + (m + 1) x - m - 2}$ có đúng hai đường tiệm cận là

A. $m \in ℝ$

B. $\{\begin{cases} [\begin{array}{l} m \geq 1 \\ m \leq - 2 \end{array} \\ m \neq - 3 \end{cases}$

C. $\{\begin{cases} m \leq - 2 \\ m \neq - 3 \end{cases}$

D. $[\begin{array}{l} m \geq 1 \\ m \leq - 2 \end{array}$

131. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x + \sqrt{m x^{2} + 1}$ có tiệm cận ngang là

A. $m > 1$

B. $0 < m < 1$

C. $m = 1$

D. $m = - 1$

132. Nhiều lựa chọn

Tập tất cả các giá trị thực của tham số m để đồ thị của hàm số $y = \frac{x - 1}{\sqrt{m x^{2} - 3 m x + 2}}$ có bốn đường tiệm cận phân biệt là

A. $(0; + \infty)$

B. $(\frac{9}{8}; + \infty)$

C. $(\frac{8}{9}; + \infty)$

D. $(\frac{8}{9}; + \infty) \ \{1\}$

133. Nhiều lựa chọn

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{1 + \sqrt{x + 1}}{\sqrt{x^{2} - (1 - m) x + 2 m}}$ có hai tiệm cận đứng?

A. 1

B. 2

C. 4

D. 3

134. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên R và $y = f^{'} (x)$ có bảng biến thiên như sau

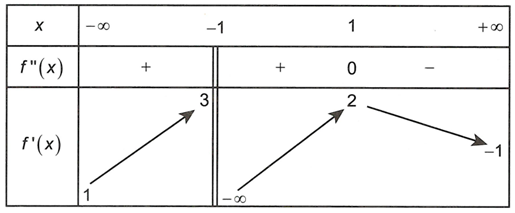
Cho hàm số y=f(x) liên tục trên R và y=f'(x) có bảng biến thiên như sau Đồ thị hàm số g(x)= 2020/f(x)-m có nhiều nhất bao nhiêu (ảnh 1)

Đồ thị hàm số $g (x) = \frac{2020}{f (x) - m}$ có nhiều nhất bao nhiêu đường tiệm cận đứng?

A. 1

B. 2

C. 3

D. 4

135. Nhiều lựa chọn

Cho hàm số $g (x) = \frac{2020}{h (x) - m^{2} - m}$ với $h (x) = m x^{4} + n x^{3} + p x^{2} + q x$ . $(m, n, p, q \in ℝ, m \neq 0)$ , $h (0) = 0$ . Hàm số $y = h^{'} (x)$ có đồ thị như hình vẽ bên dưới.

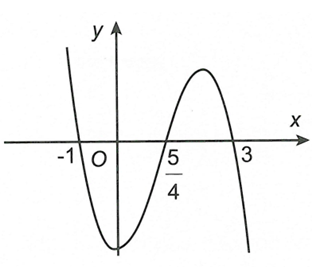
Cho hàm số g(x)=2020/h(x)-m^2-m với h(x)=mx^4+nx^3+px^2+qx . (m,n,p,q thuộc R, m khác 0) , (ảnh 1)

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $g (x)$ có hai tiệm cận đứng?

A. 2

B. 11

C. 71

D.2019

136. Nhiều lựa chọn

Cho hàm số $y = f (x)$ là hàm số bậc 3. Đồ thị hàm số $y = f^{'} (x)$ như hình vẽ dưới đây và $f (- 1) < 20$ .

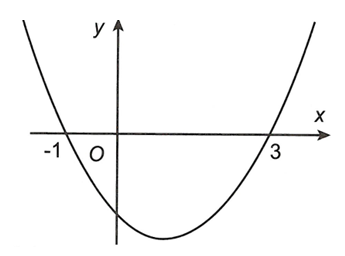
Cho hàm số y=f(x) là hàm số bậc 3. Đồ thị hàm số y=f'(x) như hình vẽ dưới đây và f(-1)<20 . (ảnh 1)

Đồ thị hàm số $g (x) = \frac{f (x) - 20}{f (x) - m}$ (m là tham số thực) có bốn tiệm cận khi và chỉ khi

A. $m < f (3)$

B. $f (3) < m < f (- 1)$

C. $m > f (- 1)$

D. $f (3) \leq m \leq f (- 1)$

137. Nhiều lựa chọn

Cho hàm số $f (x)$ liên tục trên R và $\lim_{x \to - \infty} f (x) = 1$ ; $\lim_{x \to + \infty} f (x) = + \infty$ . Có bao nhiêu giá trị nguyên của tham số m thuộc $[- 2020; 2020]$ để đồ thị hàm số $g (x) = \frac{\sqrt{x^{2} + 3 x} + x}{\sqrt{2 f (x) - f^{2} (x)} + m}$ có tiệm cận ngang nằm bên dưới đường thẳng $y = - 1$ .

A. 2

B. 0

C. 1

D. 3

138. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x - 1}{m x^{2} - 2 x + 3}$ có ba đường tiệm cận là

A. $\{\begin{cases} m < \frac{1}{5} \\ m \neq 0 \end{cases}$

B. $\{\begin{cases} m \neq 0 \\ m \neq - 1 \\ m < \frac{1}{3} \end{cases}$

C. $\{\begin{cases} m \neq 0 \\ m < \frac{1}{3} \end{cases}$

D. $\{\begin{cases} m \neq 0 \\ m \neq - 1 \\ m < \frac{1}{5} \end{cases}$

139. Nhiều lựa chọn

Có bao nhiêu giá trị của tham số m để đồ thị hàm số $y = \frac{m x^{2} - 1}{x^{2} - 3 x + 2}$ có đúng hai đường tiệm cận?

A. 3

B. 2

C. 1

D. 4

140. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x^{2} + x - 2}{x^{2} - 2 x + m}$ có ba đường tiệm cận là

A. $m < 1$

B. $m \neq 1$ và $m \neq - 8$

C. $m \leq 1$ và $m \neq - 8$

D. $m < 1$ và $m \neq - 8$

141. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x + 2}{x^{2} - 4 x + m}$ có một đường tiệm cận đứng và một đường tiệm cận ngang là

A. $m \in \{4; - 12\}$

B. $m \in [4; 12]$

C. $m = - 4$

D. $m = 12$

142. Nhiều lựa chọn

Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng $(- 10; 10)$ để đồ thị hàm số $y = \frac{6 x - 3}{(m x^{2} - 6 x + 3) (9 x^{2} + 6 m x + 1)}$ có đúng một đường tiệm cận?

A. 6

B. 7

C. 5

D. 10

143. Nhiều lựa chọn

Tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{1 + \sqrt{x + 1}}{\sqrt{x^{2} - m x - 3 m}}$ có đúng hai tiệm cận đứng là

A. $(0; \frac{1}{2})$

B. $[\frac{1}{4}; \frac{1}{2}]$

C. $(0; \frac{1}{2}]$

D. $(0; + \infty)$

144. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \sqrt{x^{2} + 1} - \frac{m}{2} x$ có tiệm cận ngang là

A. $K h ô n g t ồ n t ạ i m$

B. $m = - 2$

C. $m = - 1$ và $m = 2$

D. $m = 2$ và $m = - 2$

145. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{2 x + 1}{\sqrt{(1 - m) x^{2} + 3 x - 1}}$ có đường tiệm cận ngang là

A. $m > 1$

B. $0 < m < 1$

C. $m < 1$

D. $m \neq 1$

146. Nhiều lựa chọn

Tất cả giá trị của tham số m để đồ thị hàm số $y = \frac{\sqrt{m x^{2} + 3 m x + 1}}{x + 2}$ có ba đường tiệm cận là

A. $m \leq 0$

B. $0 < m \leq \frac{1}{2}$

C. $0 < m < \frac{1}{2}$

D. $m \geq \frac{1}{2}$

147. Nhiều lựa chọn

Tất cả giá trị của tham số m để đồ thị hàm số $y = \frac{\sqrt{x - 1} + 2019}{\sqrt{x^{2} - 2 m x + m + 2}}$ có đúng ba đường tiệm cận là

A. $m > 2$ hoặc $m < - 1$

B. $2 \leq m \leq 3$

C. $m < 2$

D. $2 < m < 3$

148. Nhiều lựa chọn

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = \frac{\sqrt{- x^{2} + 2019 x + 2020} - 12 \sqrt{70}}{x^{2} - (m + 1) x + m}$ có đúng hai đường tiệm cận?

A. 2019

B. 2018

C. 2021

D. 2020

149. Nhiều lựa chọn

Tất cả các giá trị của tham số m sao cho đồ thị của hàm số $y = \frac{x + 1}{\sqrt{m x^{2} + 1}}$ có hai tiệm cận ngang là

A. $m > 0$

B. $m < 0$

C. $m = 0$

D. không có m

150. Nhiều lựa chọn

Gọi S là tập tất cả các giá trị của tham số m để đồ thị hàm số $y = \sqrt[3]{x^{3} + 3 x^{2} + 2} - \sqrt{4 x^{2} + 3 x + 2} + m x$ có tiệm cận ngang. Tổng các phần tử của S bằng

A. -2

B. -3

C. 2

D. 3

151. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x + 1}{\sqrt{m {(x - 1)}^{2} + 4}}$ có hai tiệm cận đứng là

A. $\{\begin{cases} m < 0 \\ m \neq - 1 \end{cases}$

B. $m < 1$

C. $m < 0$

D. $m = 0$

152. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y = \frac{(m - 1) x + 1}{\sqrt{x^{2} - x} + 1}$ có đúng một đường tiệm cận ngang là

A. không có giá trị nào của m thỏa mãn.

B. $\forall m \in ℝ$

C. $m = 1$

D. $m = 0$

153. Nhiều lựa chọn

Tất cả các giá trị của tham số a để đồ thị hàm số $y = a x + \sqrt{4 x^{2} + 1}$ có tiệm cận ngang là

A. $a = - 2$ và $a = \frac{1}{2}$

B. $a = \pm \frac{1}{2}$

C. $a = \pm 2$

D. $a = \pm 1$

154. Nhiều lựa chọn

Tất cả các giá trị của tham số a để đồ thị hàm số $y = \frac{x - \sqrt{x^{2} + 1}}{\sqrt{a x^{2} + 2}}$ có tiệm cận ngang là

A. $a > 0$

B. $a = 1$ hoặc $a = 4$

C. $a \leq 0$

D. $a \geq 0$

155. Nhiều lựa chọn

Cho hàm số $y = \frac{12 + \sqrt{4 x - x^{2}}}{\sqrt{x^{2} - 6 x + 2 m}}$ có đồ thị $(C_{m})$ . Tập hợp các giá trị của tham số thực m để $(C_{m})$ có đúng hai tiệm cận đứng là

A. $(0; 9]$

B. $[8; 9)$

C. $[4; \frac{9}{2})$

D. $(4; \frac{9}{2})$

156. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{(2 m + 1) x^{2} + 3}{\sqrt{x^{4} + 1}}$ có đường tiệm cận ngang đi qua điểm $A (- 1; 3)$ là

A. m=0

B. $m = \pm 1$

C. $m = - 2$

D. $m = 2$

157. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x - 3}{\sqrt{x^{2} + m}}$ có ba tiệm cận là

A.m=0

B. $\{\begin{cases} m < 0 \\ m \neq - 9 \end{cases}$

C. $[\begin{array}{l} m = 0 \\ m = - 9 \end{array}$

D. $m > 0$

158. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị $y = \frac{m x - 3}{\sqrt{m^{2} x^{2} + 2016}}$ có hai đường tiệm cận ngang là

A. $m < 0$

B. $m = 0$

C. $m > 0$

D. $m \neq 0$

159. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{\sqrt{m x^{2} + 1}}{x + 1}$ có đúng một đường tiệm cận là

A. $- 1 \leq m < 0$

B. $- 1 \leq m \leq 0$

C. $m < - 1$

D. $m > 0$

160. Nhiều lựa chọn

Cho hàm số $f (x) = \frac{\sqrt{x - m} - 3}{x^{2} - 4 x + 3}$ có đồ thị $(C)$ . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $[- 10; 10]$ để đồ thị $(C)$ có đúng hai đường tiệm cận?

A. 3

B. 1

C. 0

D. 2

161. Nhiều lựa chọn

Cho hàm số $f (x)$ liên tục trên R và có $\lim_{x \to - \infty} f (x) = \lim_{x \to + \infty} f (x) = 2$ . Gọi S là tập hợp các giá trị của tham số m để đồ thị của hàm số $g (x) = \frac{(x - 1) [f^{2} (x) + 3]}{x^{2} + 2 (m - 1) x + m^{2} - 2}$ có tổng số tiệm cận đứng và tiệm cận ngang bằng 2. Tổng các phần tử của S bằng

A. $- \frac{1}{2}$

B. -2

C. -3

D. $\frac{3}{2}$

162. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 1}{x + 2}$ có đồ thị $(C)$ . Tọa độ giao điểm I của hai đường tiệm cận của đồ thị $(C)$ là

A. $(2; - 2)$

B. $(- 2; - 2)$

C. $(- 2; 2)$

D. $(2; 2)$

163. Nhiều lựa chọn

Giá trị của tham số m để đồ thị hàm số $y = \frac{m x - 1}{2 x + m}$ có đường tiệm cận đứng đi qua điểm $A (- 1; \sqrt{2})$ là

A. $m = - 2$

B. $m = 2$

C. $m = \sqrt{2}$

D. $m = - 1$

164. Nhiều lựa chọn

Các đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 3}{x - 1}$ tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

A. 3 (đvdt)

B. 6 (đvdt)

C. 1 (đvdt)

D. 2 (đvdt)

165. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{2 m x + m}{x - 1}$ có đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8 là

A. $m \neq \pm 2$

B. $m = 2$

C. $m = \pm \frac{1}{2}$

D. $m = \pm 4$

166. Nhiều lựa chọn

Cho đồ thị hai hàm số $f (x) = \frac{2 x + 1}{x + 1}$ và $g (x) = \frac{a x + 1}{x + 2}$ với $a \neq \frac{1}{2}$ . Tất cả các giá trị thực dương của tham số a để các tiệm cận của hai đồ thị hàm số tạo thành một hình chữ nhật có diện tích bằng 4 là

A. $a = 6$

B. $a = 4$

C. $a = 3$

D. $a = 1$

167. Nhiều lựa chọn

Cho hàm số $y = \frac{x + 1}{x - 1}$ có đồ thị $(C)$ . Hai đường tiệm cận của (C) cắt nhau tại I. Đường thẳng $d : y = 2 x + b$ (b là tham số thực) cắt đồ thị(C) tại hai điểm phân biệt A, B. Biết $b < 0$ và diện tích tam giác AIB bằng $\frac{15}{4}$ . Giá trị của b bằng

A. -1

B. -3

C. -2

D. -4

168. Nhiều lựa chọn

Trong mặt phẳng tọa độ Oxy, cho hai đường tròn $(C_{1})$ và $(C_{2})$ lần lượt có phương trình ${(x - 1)}^{2} + {(y - 2)}^{2} = 1$ và ${(x + 1)}^{2} + y^{2} = 1$ . Biết đồ thị hàm số $y = \frac{a x + b}{x + c}$ đi qua tâm của $(C_{1})$ , đi qua tâm của $(C_{2})$ và có các đường tiệm cận tiếp xúc với cả $(C_{1})$ và $(C_{2})$ . Tổng $a + b + c$ là

A. 5

B. 8

C. 2

D. 1

169. Nhiều lựa chọn

Gọi M là giao điểm của đồ thị $y = \frac{2 x - 1}{2 x + 3}$ với trục hoành. Khi đó tích các khoảng cách từ điểm M đến hai đường tiệm cận của đồ thị hàm số đã cho bằng

A. 4

B. 2

C. 8

D. 6

170. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 3}{x - 2}$ (C). Gọi M là điểm bất kỳ trên $(C)$ , d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị. Giá trị nhỏ nhất của d bằng

A. 10

B. 6

C. 2

D. 5

171. Nhiều lựa chọn

Cho hàm số $y = \frac{1 - 3 x}{3 - x}$ có đồ thị $(C)$ . Điểm M có hoành độ dương, nằm trên $(C)$ sao cho khoảng cách từ M đến tiệm cận đứng gấp hai lần khoảng cách từ M đến tiệm cận ngang của $(C)$ . Khoảng cách từ M đến tâm đối xứng của $(C)$ bằng

A. 5

B. $3 \sqrt{2}$

C. $2 \sqrt{5}$

D. 4

172. Nhiều lựa chọn

Cho hàm số $y = \frac{4 x - 5}{x + 1}$ có đồ thị (H). Gọi $M (x_{0}; y_{0})$ với $x_{0} < 0$ là một điểm thuộc đồ thị (H) thỏa mãn tổng khoảng cách từ M đến hai đường tiệm cận của (H) bằng 6. Giá trị của biểu thức $S = {(x_{0} + y_{0})}^{2}$ bằng

A. 4

B.0

C. 9

D. 1

173. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 1}{x - 1}$ có đồ thị $(C)$ . Tiếp tuyến của $(C)$ tại điểm có hoành độ bằng 3 thuộc $(C)$ cắt các đường tiệm cận của $(C)$ tạo thành tam giác có diện tích bằng

A. 4

B. $2 + \sqrt{2}$

C. $4 + 2 \sqrt{2}$

D. 2

174. Nhiều lựa chọn

Cho hàm số $y = \frac{x - 1}{2 x - 3}$ $(C)$ . Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số $(C)$ . Khoảng cách từ I đến tiếp tuyến bất kỳ của đồ thị $(C)$ đạt giá trị lớn nhất bằng

A. $\frac{1}{\sqrt{2}}$

B. 1

C. $\sqrt{2}$

D. $\sqrt{5}$

175. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 1}{x - 2}$ có đồ thị $(C)$ . Gọi I là giao điểm của hai đường tiệm cận của $(C)$ . Biết tiếp tuyến $∆$ của $(C)$ tại M cắt các đường tiệm cận đứng và tiệm cận ngang tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó, diện tích lớn nhất của tam giác tạo bởi $∆$ và hai trục tọa độ thuộc khoảng nào dưới đây?

A. $(28; 29)$

B. $(29; 30)$

C. $(27; 28)$

D. $(26; 27)$

176. Nhiều lựa chọn

Cho hàm số $y = \frac{x - 1}{x + 2}$ , gọi d là tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng $m - 2$ . Biết đường thẳng d cắt tiệm cận đứng của đồ thị hàm số tại điểm $A (x_{1}; y_{1})$ và cắt tiệm cận ngang của đồ thị hàm số tại điểm $B (x_{2}; y_{2})$ . Gọi S là tập hợp các số m sao cho $x_{2} + y_{1} = - 5$ . Tổng bình phương các phần tử của S bằng

A. 4

B. 9

C. 0

D. 10

177. Nhiều lựa chọn

Các đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 1}{x - 2018}$ cùng với hai trục tọa độ tạo thành hình chữ nhật có diện tích bằng

A. 4036.

B. 1009

C. 2018.

D. 1.

178. Nhiều lựa chọn

Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x + 1}{x + 1}$ bằng

A. $\sqrt{3}$

B. $\sqrt{2}$

C. $\sqrt{5}$

D. 5

179. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m để đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số $y = \frac{m x + 1}{2 m + 1 - x}$ cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 3 là

A. $m = 1; m = - \frac{3}{2}$

B. $m = - 1; m = 3$

C. $m = 1; m = \frac{3}{2}$

D. $m = - 1; m = - \frac{3}{2}$

180. Nhiều lựa chọn

Cho hàm số $y = \frac{m x - 1}{x - n}$ trong đó m, n là tham số. Biết giao điểm của hai đường tiệm cận của đồ thị hàm số nằm trên đường thẳng $x - 2 y + 3 = 0$ và đồ thị hàm số đi qua điểm $A (0; 1)$ . Giá trị của m+n bằng

A. -3

B. 3

C. 1

D. -1

181. Nhiều lựa chọn

Cho hàm số $y = \frac{x + 2}{x - 3}$ có đồ thị (C). Có bao nhiêu điểm M thuộc (C) sao cho khoảng cách từ điểm M đến đường tiệm cận ngang bằng 5 lần khoảng cách từ điểm M đến tiệm cận đứng?

A. 1

B. 2

C. 3

D. 4

182. Nhiều lựa chọn

Cho hàm số $y = \frac{x + 1}{x - 1}$ có đồ thị $(C)$ và A là điểm thuộc $(C)$ . Giá trị nhỏ nhất của tổng các khoảng cách từ A đến các đường tiệm cận của $(C)$ bằng

A. $2 \sqrt{2}$

B. 2

C. 3

D. $2 \sqrt{3}$

183. Nhiều lựa chọn

Cho hàm số $y = \frac{x + 2}{x - 2}$ có đồ thị là $(C)$ . Tọa độ điểm M có hoành độ dương thuộc $(C)$ sao cho tổng khoảng cách từ M đến hai tiệm cận nhỏ nhất là

A. $(0; - 1)$

B. $(2; 2)$

C. $(1; - 3)$

D. $(4; 3)$

184. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 2}{x - 2}$ có đồ thị $(C)$ . M là điểm thuộc $(C)$ sao cho tiếp tuyến của $(C)$ tại M cắt hai đường tiệm cận của $(C)$ tại hai điểm A, B thỏa mãn $A B = 2 \sqrt{5}$ . Tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán bằng

A. 5

B. 8

C. 7

D. 6

185. Nhiều lựa chọn

Cho hàm số $y = \frac{x + 2}{x + 1}$ có đồ thị (C). Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị (C) đến một tiếp tuyến của (C). Giá trị lớn nhất của d bằng

A. $\sqrt{2}$

B. $3 \sqrt{3}$

C. $\sqrt{3}$

D. $2 \sqrt{2}$

186. Nhiều lựa chọn

Cho hàm số $y = \frac{x - 3}{x + 1}$ có đồ thị là $(C)$ . Gọi I là giao điểm của hai đường tiệm cận của $(C)$ . Các điểm M trên $(C)$ sao cho độ dài đoạn IM ngắn nhất là

A. $M_{1} (1; 1)$ và $M_{2} (- 3; 0)$

B. $M_{1} (1; - 1)$ và $M_{2} (- 3; 3)$

C. $M_{1} (1; - 1)$ và $M_{2} (- 3; 2)$

D. $M_{1} (1; - 2)$ và $M_{2} (- 3; - 3)$

187. Nhiều lựa chọn

Cho đồ thị $(C)$ : $y = \frac{2 x + 1}{x - 1}$ . Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm hai đường tiệm cận của (C)). Diện tích tam giác GPQ là

A. 2

B. 4

C. $\frac{2}{3}$

D. 1

188. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 1}{x + 1}$ có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận và $M (x_{0}, y_{0}) (x_{0} > 0)$ là một điểm trên (C) sao cho tiếp tuyến của tại M cắt hai đường tiệm cận lần lượt tại A, B thỏa mãn $A I^{2} + I B^{2} = 40$ . Khi đó tích $x_{0} y_{0}$ bằng

A. $\frac{1}{2}$

B. 2

C. 1

D. $\frac{15}{4}$

189. Nhiều lựa chọn

Tất cả giá trị thực của tham số m để đồ thị hàm số $f (x) = \frac{x + 1}{x^{2} + m x + 1}$ có hai đường tiệm cận đứng là các đường thẳng $x = x_{1}$ và $x = x_{2}$ sao cho $\frac{x_{1}^{2}}{x_{2}^{2}} + \frac{x_{2}^{2}}{x_{1}^{2}} > 7$ là

A. $[\begin{array}{l} m > 2 \\ m < - 2 \end{array}$

B. $- 2 < m < 2$

C. $[\begin{array}{l} 2 < m > \sqrt{5} \\ - \sqrt{5} < m < - 2 \end{array}$

D. $[\begin{array}{l} m > \sqrt{5} \\ m < - \sqrt{5} \end{array}$

190. Nhiều lựa chọn

Biết rằng đồ thị của hàm số $f (x) = \frac{x - 1}{x^{2} + m x + n}$ có hai tiệm cận đứng là $x = x_{1}$ và $x = x_{2}$ sao cho $\{\begin{cases} x_{1} - x_{2} = 5 \\ x_{1}^{3} - x_{2}^{3} = 35 \end{cases}$ . Giá trị m+n bằng

A. -1

B. -7

C. 1

D. 7

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube