25 CÂU HỎI
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6x + 3y - 2z - 6 = 0
B. x + 2y + 3z - 14 = 0
C. x + 3y + 2z - 11 = 0
Trong không gian Oxyz, cho ba điểm A(0;0;-1), B(-1;1;0), C(1;0;1). Tìm điểm M sao cho 3MA2 + 2MB2 - MC2 đạt giá trị nhỏ nhất.
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
A. a + b + c = 12
B. a2 + b = c - 6
C. a + b + c = 18
D. a + b - c = 0
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
A. arccos(4/15)
B. 1
C. arcsin(4/5)
D. arccos(4/5)
Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A, B, C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
A. 2x + y + z - 6 = 0
B. x + 2y + z - 6 = 0
C. x + 2y + 2z - 6 = 0
D. 2x + y + z + 6 = 0
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 0; -2), B(4; 0; 0). Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:
A. I (0;0;-1)
B. I (2;0;0)
C. I (2;0;-1)
D. I (4/3;0;-2/3)
Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;-3;0) và mặt phẳng (P): x + y + z - 3 = 0. Tìm trên (P) điểm M sao cho nhỏ nhất.
A. M (3;3;-3)
B. M (-3;-3;3)
C. M (3;-3;3)
D. M (-3;3;3)
Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. 2x + y - 3z + 3 = 0
B. x + 2y - z - 1 = 0
C. 3x + 2y - z + 1 = 0
D. 2x - y - 3z + 3 = 0
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và
Mặt cầu có một đường kính là đoạn thẳng vuông góc chung của d1 và d2 có phương trình là:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
A. 4a/3
B. a/3
C. 2a/3
D. 3a/4
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
A. M (0;1;-4)
B. M (2;1;0)
C. M (0;1;-2)
D. M (0;1;4)
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
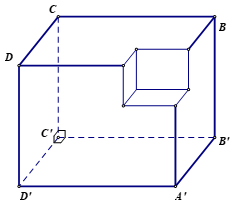
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 2; 3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
A. 1372/9
B. 686/9
C. 524/3
D. 343/9
Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB = 2a, AD = a. Gọi K là điểm thuộc BC sao cho . Tính khoảng cách giữa hai đường thẳng AD và SK.
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức AM2 + BM2 = 30 là một mặt cầu (S). Tọa độ tâm I và bán kính R của mặt cầu (S) là:
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1;0;0), B(0;1;0), C(0;0;1), D(0;0;0). Hỏi có bao nhiêu điểm cách đều 4 mặt phẳng (ABC), (CDA), (BCD), (DAB).
A. 4
B. 5
C. 1
D. 8
Trong không gian Oxyz, cho tứ diện S.ABC có S(0;0;1), A(1;0;1), B(0;1;1), C (0;0;2). Hỏi tứ diện S.ABC có bao nhiêu mặt phẳng đối xứng?
A. 6
B. 1
C. 0
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là: .
Cho ba điểm A, M, B nằm trên mặt cầu (S) sao cho góc AMB = . Diện tích tam giác AMB có giá trị lớn nhất bằng?
A. 4
B. 2
C. 4π
D. Không tồn tại.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2;1;3), B(1;-1;2), C(3;-6;1). Điểm M(x;y;z) thuộc mặt phẳng (Oyz) sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất. Tính giá trị của biểu thức P = x+y+z
A. P = 0
B. P = 2P = 0
C. P = 6
D. P = -2
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
A. a+b+c=6
B. a+b+c=5
C. a+b+c=8
D. a+b+c=7
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD', điểm N thuộc đoạn BD sao cho AM = DN = x, (0 < x < a√2/2). Tìm x theo a để đoạn MN ngắn nhất.
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5) và D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?
A. Có vô số mặt phẳng.
B. 1 mặt phẳng.
C. 7 mặt phẳng.
D. 4 mặt phẳng.
Trong không gian Oxyz, cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của đường thẳng d là:
Trong không gian Oxyz, cho hai điểm A(-1;2;1), B(1;2;-3) và đường thẳng d: . Tìm vectơ chỉ phương của đường thẳng Δ đi qua điểm A và vuông góc với d đồng thời cách B một khoảng lớn nhất.
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9


