12 CÂU HỎI
Cho hàm số \({\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + {\rm{d}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R},{\rm{a}} \ne 0)\) có bảng xét dấu của đạo hàm dưới đây
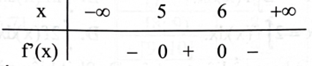
Hàm số đã cho đồng biến trên khoảng
A. \(( - \infty ;5).\)
B. \((5;6).\)
C. \((5; + \infty ).\)
D. \((6; + \infty ).\)
Cho hàm số \({\rm{f}}({\rm{x}})\) có bảng biến thiên như hình sau. Điểm cực đại của hàm số là
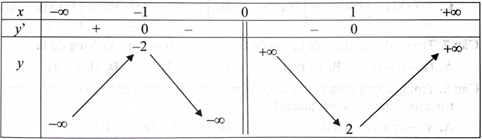
A. xCĐ = -1
B. xCĐ = 1
C. xCĐ = -2
D. xCĐ = 2
Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng
![Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727150158.png)
A. -1
B. 0.
C. 1.
D. 2.
Cho hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\) \(({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R},{\rm{ac}} \ne 0)\) có đồ thị như hình bên. Đường tiệm cận đứng của đồ thị hàm số là
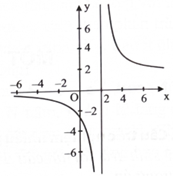
A. \({\rm{y}} = - 2.\)
B. \({\rm{y}} = 2.\)
C. \({\rm{x}} = - 2.\)
D. \({\rm{x}} = 2.\)
Cho \({\rm{f}}({\rm{x}})\) là hàm số liên tục trên \(\mathbb{R}.\) Phát biểu nào sau đây là đúng?
A. \(\int 2 f(x)dx = - 2\int f (x)dx.\)
B. \(\int 2 f(x)dx = 2 + \int f (x)dx.\)
C. \(\int 2 f(x)dx = 2\int f (x)dx.\)
D. \(\int 2 f(x)dx = 2 - \int f (x)dx.\)
Cho \({\rm{f}}({\rm{x}})\) là hàm số liên tục trên \(\mathbb{R}.\) Phát biểu nào sau đây là đúng?
A. \(\int_3^4 f (x)dx \cdot \int_4^5 f (x)dx = \int_3^5 f (x)dx\)
B. \(\int_3^4 f (x)dx - \int_4^5 f (x)dx = \int_3^5 f (x)dx.\)
C. \(\int_3^4 f (x)dx + \int_4^5 f (x)dx = \int_5^3 f (x)dx.\)
D. \(\int_3^4 f (x)dx + \int_4^5 f (x)dx = \int_3^5 f (x)dx.\)
Trong không gian với hệ tọa độ Oxyz, vectơ \(\overrightarrow {\rm{u}} = \overrightarrow {\rm{i}} - \overrightarrow {\rm{j}} - \overrightarrow {\rm{k}} \) có tọa độ là
A. \((1; - 1; - 1).\)
B. \((1;1;1).\)
C. \((1; - 1;1).\)
D. \((1;1; - 1).\)
Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình tổng quát của mặt phẳng?
A. \({x^2} - 4y + 5z - 6 = 0\)
B. \(3x - {y^4} + 5z - 6 = 0.\)
C. \(3x - 4y + 5z - 6 = 0.\)
D. \(3x - 4y + {z^5} - 6 = 0.\)
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình của mặt cầu?
A. \( - {(x - 1)^2} + {(y + 1)^2} + {(z - 10)^2} = 225.\)
B. \({({\rm{x}} - 1)^2} - {({\rm{y}} + 1)^2} + {({\rm{z}} - 10)^2} = 225.\)
C. \({({\rm{x}} - 1)^2} + {({\rm{y}} + 1)^2} - {({\rm{z}} - 10)^2} = 225.\)
D. \({({\rm{x}} - 1)^2} + {({\rm{y}} + 1)^2} + {({\rm{z}} - 10)^2} = 225.\)
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng?
A. \(\frac{{x - 9}}{3} = \frac{{y - 1}}{{11}} = \frac{{z + 7}}{{14}}.\)
B. \(\frac{{x - 1}}{{4y}} = \frac{{y - 2}}{5} = \frac{{z + 3}}{6}.\)
C. \(\frac{{{\rm{x}} + 7}}{{10}} = \frac{{{\rm{y}} + 8}}{{11{\rm{z}}}} = \frac{{{\rm{z}} + 9}}{{12}}.\)
D. \(\frac{{{\rm{x}} - 13}}{{16}} = \frac{{{\rm{y}} - 14}}{{17}} = \frac{{{\rm{z}} - 15}}{{18{\rm{z}}}}.\)
Cho các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,2;{\rm{P}}({\rm{B}}) = 0,4.\) Xác suất của biến cố A với điều kiện B bằng
A. 0,2.
B. 0,08.
C. 0,6.
D. 0,5.
Khi thống kê kết quả thi thử của 100 học sinh ở một trung tâm giáo dục, người ta được bảng thống kê tần số ghép nhóm như hình bên. Số trung bình của mẫu số liệu là
|
Điểm |
Giá trị đại diện |
Tần số |
|
\([3;4)\) |
3,5 |
2 |
|
\([4;5)\) |
4,5 |
7 |
|
\([5;6)\) |
5,5 |
21 |
|
\([6;7)\) |
6,5 |
26 |
|
\([7;8)\) |
7,5 |
29 |
|
\([8;9)\) |
8,5 |
12 |
|
[9 ; 10] |
9,5 |
3 |
|
|
|
n = 100 |
A. 6,73.
B. 6,7.
C. 6,72.
D. 6,71.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
