12 CÂU HỎI
Trong các hình dưới đây, có một hình là đồ thị của hàm số \({\rm{y}} = {{\rm{a}}^{\rm{x}}}(0 < {\rm{a}} < 1)\), hình đó là hình nào?
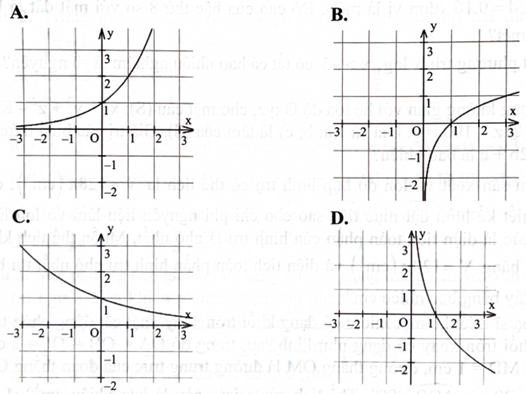
A. Hình A
B. Hình B
C. Hình C
D. Hình D
Trong không gian với hệ toạ độ Oxyz, toạ độ của vectơ \(\vec u = 3\vec i - \vec j - 2\vec k\) là
A. \((3; - 1; - 2).\)
B. \((3;1; - 2).\)
C. \((3; - 1;2).\)
D. \((3;1;2).\)
Nếu hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có một nguyên hàm là hàm số \({\rm{y}} = {\rm{F}}({\rm{x}})\) thì giá trị của biểu thức \(\int_5^3 {\rm{f}} ({\rm{x}}){\rm{dx}}\) bằng
A. \(F(5) - F(3).\)
B. \(F(3) - F(5).\)
C. \(F(3).\) \(F(5).\)
D. \(F(3):F(5).\)
Nếu hàm số \(y = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}}\), \({\rm{n}} \in \mathbb{R}\) ) có đồ thị như hình bên thì có điểm cực tiểu là
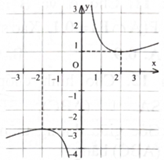
A. 1.
B. -1.
C. 2.
D. -2.
Đạo hàm của hàm số \({\rm{f}}({\rm{x}}) = \cos 5{\rm{x}}\) là
A. \({\rm{f}}({\rm{x}}) = 5\sin 5{\rm{x}}.\)
B. \(f(x) = - \sin 5x.\)
C. \({\rm{f}}({\rm{x}}) = \sin 5{\rm{x}}.\)
D. \(f(x) = - 5\sin 5x.\)
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm \({\rm{M}}({\rm{a}};{\rm{b}};{\rm{c}})\) và nhận \(\vec n = (2; - 3;4)\) là vectơ pháp tuyến có phương trình là
A. \(a(x - 2) + b(y + 3) + c(z - 4) = 0.\)
B. \(2(x - a) - 3(y - b) + 4(z - c) = 0.\)
C. \(a(x - 2) + b(y - 3) + c(z - 4) = 0.\)
D. \(2(x - a) + 3(y - b) + 4(z - c) = 0.\)
Trong không gian với hệ tọa độ Oxyz, nếu \(\varphi \) là góc giữa đường thẳng \(\frac{{{\rm{x}} - {\rm{x}}0}}{{\rm{a}}} = \frac{{{\rm{y}} - {\rm{y}}0}}{{\;{\rm{b}}}} = \frac{{{\rm{z}} - {{\rm{z}}_0}}}{{\rm{c}}}\) và mặt phẳng \({\rm{Ax}} + {\rm{By}} + {\rm{Cz}} + {\rm{D}} = 0\) thì giá trị của biểu thức \(\frac{{|{\rm{aA}} + {\rm{bB}} + {\rm{cC}}|}}{{\sqrt {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} \cdot \sqrt {{{\rm{A}}^2} + {{\rm{B}}^2} + {{\rm{C}}^2}} }}\) bằng
A. \(\cos \varphi .\)
B. \(\tan \varphi .\)
C. \(\cot \varphi .\)
D. \(\sin \varphi .\)
Trong không gian với hệ toạ độ Oxyz mặt cầu \({({\rm{x}} - 5)^2} + {({\rm{y}} + 8)^2} + {({\rm{z}} - 13)^2} = {9^2}\) có toạ độ tâm là
A. \((5;8;13).\)
B. \((5; - 8;13).\)
C. \(( - 5;8; - 13).\)
D. \(( - 5; - 8; - 13).\)
Phát biểu nào sau đây là đúng?
A. \(\int 1 {2^{\rm{x}}}{\rm{dx}} = {12^{\rm{x}}}.\)
B. \(\int 1 {2^{\rm{x}}}{\rm{dx}} = \frac{{{{12}^{\rm{x}}}}}{{\ln 12}}.\)
C. \(\int 1 {2^{\rm{x}}}{\rm{dx}} = \frac{{{{12}^{\rm{x}}}}}{{\ln 12}} + \) C.
D. \(\int 1 {2^{\rm{x}}}{\rm{dx}} = {12^{\rm{x}}} + \) C.
Khi thống kê chiều cao (đơn vị là cm ) học sinh của lớp 12 A, người ta sử dụng mẫu số liệu ghép nhóm và được một kết quả cho bởi Bảng 1. Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng
|
Nhóm |
Tần số |
|
\([155;160)\) |
2 |
|
\([160;165)\) |
5 |
|
\([165;170)\) |
21 |
|
\([170;175)\) |
11 |
|
\([175;180)\) |
1 |
|
|
\({\rm{n}} = 40\) |
A. 25.
B. 5.
C. 20.
D. 180.
Cho A và B là hai biến cố thoả mãn \({\rm{P}}({\rm{A}}) = 0,6,{\rm{P}}({\rm{B}}) = 0,2\) và \({\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,1.\) Xác suất \({\rm{P}}({\rm{A}} \cup {\rm{B}})\) bằng
A. 0,9.
B. 0,012.
C. 0,8.
D. 0,7.
Cho hình chóp S.ABC thoả mãn \({\rm{SA}} \bot ({\rm{ABC}}),\widehat {{\rm{SBA}}} = {40^o },\widehat {{\rm{SCA}}} = {35^o }.\)
Góc giữa đường thẳng SB và mặt phẳng \(({\rm{ABC}})\) bằng
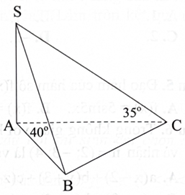
A. \({40^o }.\)
B. \({35^o }.\)
C. \({50^o }.\)
D. \({55^o }.\)
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
