12 CÂU HỎI
Biết rằng đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}(a,b,c,d \in \mathbb{R})\) ở hình bên có tâm đối xứng là một trong bốn điểm sau đây, điểm đó là điểm nào?
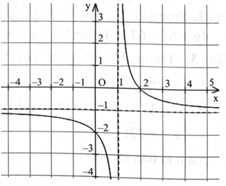
A. \({\rm{M}}(0; - 1).\)
B. \({\rm{N}}(1;0).\)
C. \({\rm{P}}(1; - 1).\)
D. \({\rm{Q}}( - 1;1).\)
Một trong bốn hình sau đây là đồ thị hàm số \({\rm{y}} = {\log _{\rm{a}}}{\rm{x}}\) với \(0 < {\rm{a}} < 1.\) Hình đó là hình nào?
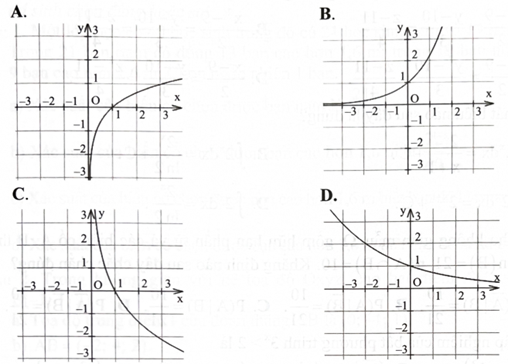
A. Hình A
B. Hình B
C. Hình C
D. Hình D
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Số đo góc nhị diện \(\left[ {{C^\prime },{\rm{AB}},{\rm{C}}} \right]\) bằng
![Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Số đo góc nhị diện \(\left[ {{C^\prime },{\rm{AB}},{\rm{C}}} \right]\) bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727161807.png)
A. \({30^o }.\)
B. \({45^o }.\)
C. \({60^o }.\)
D. \({90^o }.\)
Tất cả các nghiệm của phương trình \(\tan x = - \sqrt 3 \) là
A. \(\frac{{ - \pi }}{3} + {\rm{k}}\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
B. \(\frac{{ - \pi }}{3} + {\rm{k}}2\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
C. \(\frac{{ - \pi }}{3} + {\rm{k}}3\pi ,\forall {\rm{k}} \in \mathbb{Z}.\)
D. \(\frac{{ - \pi }}{3} + \frac{{{\rm{k}}\pi }}{2},\forall {\rm{k}} \in \mathbb{Z}.\)
Trong không gian với hệ toạ độ Oxyz, tích vô hướng của hai vectơ \(\overrightarrow {\rm{a}} = (1; - 3;5),\overrightarrow {\rm{b}} = ({\rm{m}};{\rm{n}};{\rm{p}})\) bằng
A. \(m + 3n + 5p.\)
B. \(|m - 3n + 5p|.\)
C. \(\sqrt {{1^2} + {{( - 3)}^2} + {5^2}} \cdot \sqrt {{{\rm{m}}^2} + {{\rm{n}}^2} + {{\rm{p}}^2}} .\)
D. \(m - 3n + 5p.\)
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình chính tắc của một đường thẳng?
A. \(\frac{{{\rm{x}} - 9}}{2} = \frac{{{\rm{y}} - 10}}{3} = \frac{{{\rm{z}} - 11}}{4}.\)
B. \(\frac{{{x^2} - 9}}{2} = \frac{{y - 10}}{3} = \frac{{z - 11}}{4}.\)
C. \(\frac{{{\rm{x}} - 9}}{2} = \frac{{{{\rm{y}}^2} - 10}}{3} = \frac{{{\rm{z}} - 11}}{4}.\)
D. \(\frac{{{\rm{x}} - 9}}{2} = \frac{{{\rm{y}} - 10}}{3} = \frac{{{{\rm{z}}^2} - 11}}{4}.\)
Phát biểu nào sau đây là đúng?
A. \(\int {{2^x}} dx = \frac{{{2^{x + 1}}}}{{x + 1}} + C.\)
B. \(\int {{2^{\rm{x}}}} {\rm{dx}} = \frac{{{2^{\rm{x}}}}}{{\ln 2}} + C.\)
C. \(\int {{2^x}} dx = {2^{x + 1}} + C.\)
D. \(\int {{2^{\rm{x}}}} {\rm{dx}} = \frac{{{2^{\rm{x}}}}}{{\ln 2}}.\)
Cho không gian mẫu \(\Omega \) gồm hữu hạn phần tử và các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{n}}({\rm{B}}) = 21,{\rm{n}}({\rm{A}} \cap {\rm{B}}) = 10.\) Khẳng định nào sau đây chắc chắn đúng?
A. \({\rm{P}}(\overline {\rm{A}} \mid {\rm{B}}) = \frac{{10}}{{21}}.\)
B. \({\rm{P}}({\rm{A}}\mid \overline {\rm{B}} ) = \frac{{10}}{{21}}.\)
C. \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = \frac{{10}}{{21}}.\)
D. \({\rm{P}}(\overline {\rm{A}} \mid \overline {\rm{B}} ) = \frac{{10}}{{21}}.\)
Tập nghiệm của bất phương trình \({3^x} > 2\) là
A. \(\left( { - \infty ;{3^2}} \right).\)
B. \(\left( {{{\log }_3}2; + \infty } \right).\)
C. \(\left( { - \infty ;{{\log }_3}2} \right).\)
D. \(\left( {{3^2}; + \infty } \right).\)
Trong không gian với hệ tọa độ Oxyz, mặt cầu tâm \({\rm{I}}(9; - 8;7)\) bán kính 16 có phương trình là
A. \({({\rm{x}} - 9)^2} + {({\rm{y}} + 8)^2} + {({\rm{z}} - 7)^2} = {16^2}.\)
B. \({({\rm{x}} - 9)^2} + {({\rm{y}} + 8)^2} + {({\rm{z}} - 7)^2} = 16.\)
C. \({(x + 9)^2} + {(y - 8)^2} + {(z + 7)^2} = {16^2}.\)
D. \({(x + 9)^2} + {(y - 8)^2} + {(z + 7)^2} = 16.\)
Nếu hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) thoả mãn \(\int_5^6 f (x)dx = 2,\int_5^7 f (x)dx = 8\) thì \(\int_6^7 f (x)dx\) bằng
A. 16.
B. 6
C. 10.
D. 4.
Xét mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, tứ phân vị thứ hai, tứ phân vị thứ ba lần lượt là 3,6 và 8. Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng
A. 3.
B. 2.
C. 5.
D. 17.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
