50 CÂU HỎI
Trong không gian Oxyz, cho đường thẳng d vuông góc với mặt phẳng . Véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng d?
A.
B.
C.
D.
Cho hàm số liên tục tại và có bảng biến thiên sau.
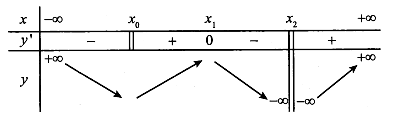
Đồ thị hàm số đã cho có
A. hai điểm cực trị, một điểm cực tiểu.
B. một điểm cực đại, không có điểm cực tiểu.
C. một điểm cực đại, hai điểm cực tiểu.
D. một điểm cực đại, một điểm cực tiểu
Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Điểm A trong hình vẽ bên biểu diễn cho số phức z. Tìm phần thực và phần ảo của số phức .
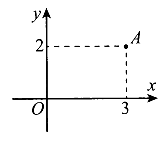
A. Phần thực là -3 và phần ảo là 2.
B. Phần thực là 3 và phần ảo là -2.
C. Phần thực là 3 và phần ảo là -2i.
D. Phần thực là -3 và phần ảo là 2i.
Cho hàm số có bảng biến thiên như hình vẽ sau.
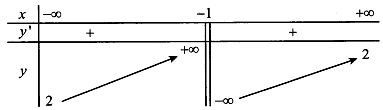
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên
B. Hàm số đồng biến trên .
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên R
Cho ba điểm và đường thẳng . Tìm điểm D có hoành độ dương trên d sao cho tứ diện ABCD có thể tích bằng 12.
A.
B.
C.
D.
Đặt thì trở thành
A.
B.
C.
D.
Cho hàm số . Biết hàm số có hai điểm cực trị là x=1 ,x=2 và f(0)=1 . Giá trị của biểu thức là
A. P = -2
B. P = 0
C. P = -1
D. P = 5
Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc . Thể tích V của khối chóp là
A.
B.
C.
D.
Cho hàm số y = f(x) có đạo hàm . Số điểm cực trị của hàm số là
A. 1
B. 2
C. 3
D. 4
Cho . Hãy biểu diễn ln30 theo m và n.
A.
B.
C.
D.
Với và a là tham số, đặt . Hàm số f(x) đồng biến trên khoảng nào trong các khoảng sau đây?
A. (1;e)
B.
C.
D.
Một hình nón có bán kính đáy bằng 1 và thiết diện qua trục là một tam giác vuông cân. Diện tích xung quanh của hình nón bằng
A.
B.
C.
D.
Trong không gian Oxyz, phương trình mặt cầu đi qua bốn điểm O, và là
A.
B.
C.
D.
Cho hàm số f(x) có bảng biến thiên như sau.
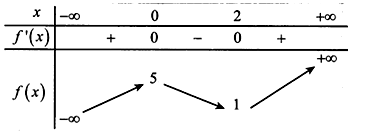
Khẳng định nào sau đây là đúng?
A. Giá trị cực đại của hàm số bằng 1.
B. Giá trị cực đại của hàm số bằng 5.
C. Giá trị cực tiểu của hàm số bằng 2.
D. Giá trị cực đại của hàm số bằng 0
Buổi sáng ông Tần vừa nhập một lượng dưa hấu từ nông dân và bán cho khách. Ông thống kê lại số dưa bán được theo giờ. Giờ thứ nhất bán được nửa số dưa và nửa quả, giờ thứ hai bán được nửa số dưa còn lại và nửa quả, giờ thứ 3 bán được nửa số dưa còn lại và nửa quả… Đến giờ thứ 5 sau khi bán được nửa số dưa còn lại và nửa quả thì ông còn dư 1 quả. Hỏi buổi sáng ông Tần đã nhập vào bao nhiêu quả dưa hấu?
A. 127 quả
B. 63 quả
C. 45 quả
D. 105 quả
Cho hình chóp S.ABCD có đáy là hình vuông. Trên AB lấy một điểm M. Gọi là mặt phẳng qua M và song song với mặt phẳng cắt SB, SC và CD lần lượt tại N, P, Q. Thiết diện của với hình chóp là
A. hình thoi MNPQ.
B. hình thang MNPQ.
C. hình thang cân MNPQ.
D. hình bình hà
Kí hiệu là hai nghiệm phức của phương trình . Giá trị của bằng
A.
B.
C. 3
D. 10
Trong các hàm số sau hàm số nào là đạo hàm của hàm số ?
A.
B.
C.
D.
Cho hàm số 7-f(x) có đồ thì hàm số y=f'(x) như hình vẽ. Biết f(a) >0 . Hỏi đồ thị hàm số có tối đa bao nhiêu điểm cực trị?
A. 3
B. 4
C. 5
D. 7
Một cốc nước hình trụ có chiều cao là (cm) bên trong đựng một lượng nước. Biết rằng khi nghiêng chiếc cốc sao cho lượng nước chạm mép cốc thì đồng thời nước cũng vừa chạm vào bán kính đáy cốc. Hỏi khi nghiêng cốc sao cho lượng nước vừa đủ phủ kín đáy cốc thì điểm còn lại mà lượng nước chạm vào thành cốc cách đáy cốc một khoảng bằng bao nhiêu?
A.
B.
C. 4 cm
D. 3cm
Cho hình trụ có hai đáy là hai đường tròn (O) và (O'), chiều cao bằng 2R và bán kính đáy R. Một mặt phẳng đi qua trung điểm của OO' và tạo với một góc , cắt đường tròn đáy theo một dây cung có độ dài bằng
A.
B.
C.
D.
Tập nghiệm S của phương trình là
A.
B.
C.
D.
Cho x, y () là hai số thực dương thỏa mãn . Giá trị của biểu thức là
A. P = 17
B. P = 50
C. P = 51
D. P = 40
Cho số phức z thỏa mãn |z|=2 . Tập hợp điểm biểu diễn số phức là
A. một đường tròn.
B. một đường thẳng.
C. một Elip.
D. một parabol hoặc hyperbol.
Cho hàm số y=f(x) là hàm đa thức bậc 5 có đồ thị hàm số y=f'(x) như hình vẽ. Hàm số y=f(x) đồng biến trên những khoảng nào trong các khoảng sau đây?
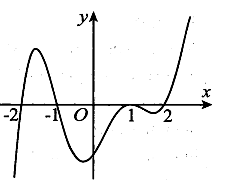
A. và
B.( ) và (-1;2)
C. và
D. và
Cho thỏa mãn . Biết phương trình có nghiệm duy nhất . Giá trị của biểu thức là
A. T = 2020
T= 1
D.
D.
Trong một lớp học có 35 học sinh. Muốn chọn ra một lớp trưởng, một lớp phó thì số cách chọn là
A.
B.
C.
D.
Cho hàm số có đạo hàm liên tục trên R và hàm số có đồ thị trên đoạn như hình vẽ. Biết diện tích miền màu xám là , giá trị tích phân là
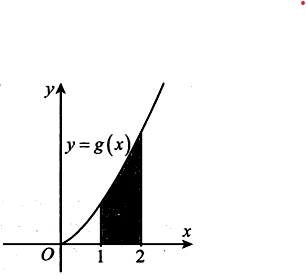
A.
B.
C. I = 5
D. I =10
Trong không gian với hệ tọa độ Oxyz, gọi là mặt phẳng chứa đường thẳng và vuông góc với mặt phẳng . Giao tuyến của và đi qua điểm nào dưới đây?
A. (0;1;3)
B. (2;3;3)
C. (5;6;8)
D. (1;-2;0)
Một chiếc cốc có dạng hình trụ, chiều cao là 16cm, đường kính đáy bằng 8cm, bề dày thành cốc và đáy cốc là 1cm. Nếu đổ một lượng nước vào cốc cách miệng cốc 5cm thì ta được khối nước có thể tích , nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích . Tỉ số bằng
A.
B.
C.
D.
Cho hàm số y= f(x) đồng biến trên ; y =f(x) liên tục, nhận giá trị dương trên và thỏa mãn và . Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Cho tam giác ABC đều cạnh a. Gọi (P) là mặt phẳng chứa BC và vuông góc với (ABC) . Trong (P) xét đường tròn (C) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C) và đỉnh A bằng
A.
B.
C.
D.
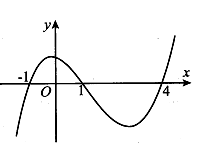 Cho hàm số y = f(x) . Hàm số có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng
Cho hàm số y = f(x) . Hàm số có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng
A.
B.
C. (-1;1)
D.
Tại sân ga, có một đoàn tàu gồm 8 toa. Có 5 hành khách lên tàu, độc lập với nhau, mỗi người lên 1 toa ngẫu nhiên. Xác suất để sau khi hành khách lên tàu, đoàn tàu còn 7 toa trống là
A.
B.
C.
D.
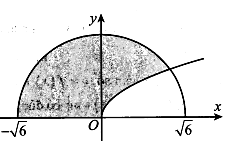
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số , cung tròn có phương trình và tục hoành (phần tô đậm trong hình vẽ bên). Thể tích V của vật thể tròn xoay sinh ra khi quay hình phẳng D quanh trục Ox là
A.
B.
C.
D.
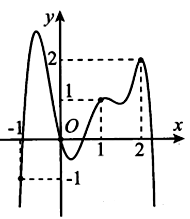 Cho hàm số có đồ thị như hình vẽ bên. Đặt . Biết rằng . Khẳng định nào dưới đây là đúng?
Cho hàm số có đồ thị như hình vẽ bên. Đặt . Biết rằng . Khẳng định nào dưới đây là đúng?
A.
B.
C.
D.
Xét các số phức z, w thỏa mãn . Gọi lần lượt là các số phức mà tại đó đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Môđun bằng
A.
B. 3
C. 6
D.
Cho lăng trụ đều tam giác ABCA'B'C' có cạnh AB=2a, M là trung điểm của A'B', . Thể tích khối lăng trụ ABC.A'B'C' bằng
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên để phương trình có hai nghiệm phân biệt?
A. 2016
B. 2017
C. 2018
D.2019
Trong không gian Oxyz, cho điểm A(10;2;1) và đường thẳng . Gọi (P) là mặt phẳng đi qua điểm A, song song với đường thẳng d sao cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm đến mặt phẳng (P) là
A.
B.
C.
D.
Cho tứ diện ABCD có AB=CD=a;AC=BD=b;AD=BC=c . Giá trị côsin góc giữa hai đường thẳng AC và BD bằng
A.
B.
C.
D.
Trong không gian Oxyz, cho đường thẳng và mặt cầu . Hai điểm A và B thay đổi trên (S) sao cho tiếp diện của tại A và B vuông góc với nhau. Đường thẳng qua A song song với d cắt mặt phẳng (Oxy) tại M, đường thẳng B song song với d cắt mặt phẳng (Oxy) tại N. Giá trị lớn nhất của tổng AM+BN bằng
A.
B.
C.
D.
Cho hàm số y=f(x) có đồ thị như hình vẽ. Tất cả giá trị của tham số m để đồ thị hàm số có đúng 3 điểm cực trị là
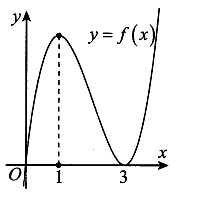
A.
B.
C.
D.
Cho đồ thị ; và điểm . Lấy , các tia đối của tia IA, IB cắt lần lượt tại C và D sao cho . Diện tích tam giác IAB bằng
A.
B. 250
C.
D. 505
Cho phương trình với m là tham số thực. Có tất cả bao nhiêu giá trị của để phương trình đã cho có nghiệm trên đoạn [2;4]?
A. 1280
B. 1285
C. 1287
D. 1286
Cho là hàm số chẵn liên tục trong đoạn và . Giá trị tích phân là
A. I = 2019
B. I = 2020
C. I=2021
D. I= 2018
Cho hàm số có bảng biến thiên như sau.
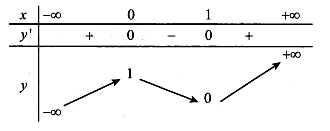
Tìm m để phương trình có bốn nghiệm phân biệt .
A.
B.
C.
D.
Cho ba điểm A, B, C lần lượt là 3 điểm biểu diễn của các số phức thỏa mãn điều kiện và . Giá trị lớn nhất của diện tích tam giác ABC bằng
A.
B.
C.
D.
Trong không gian Oxyz, cho điểm A(0;0;6) , điểm M nằm trên mặt phẳng (Oxy) và . Gọi D là hình chiếu vuông góc của O lên AM và E là trung điểm của OM. Biết đường thẳng DE luôn tiếp xúc với một mặt cầu cố định. Bán kính mặt cầu đó là
A. R=2
B. R=1
C. R=3
D.


