Quiz

30 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài tập cuối chương 8 có đáp án

Admin30 câu hỏiToánLớp 7

Bắt đầu ngay

30 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hình vẽ như bên dưới. Khi đó:

Cho hình vẽ như bên dưới. Khi đó: A. AE là đường trung trực của BC; (ảnh 1)

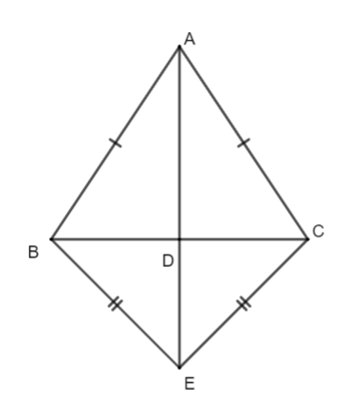
A. AE là đường trung trực của BC;

B. D là trung điểm của AE;

C. D cách đều hai điểm A và E;

D. Tất cả đáp án trên đều sai

2. Nhiều lựa chọn

Cho tam giác ABC nhọn có đường trung trực AD với D nằm trên BC. Khi đó:

A. AD là tia phân giác góc $\hat{B A C}$ ;

B. ∆ABC vuông cân tại A;

C. ∆ABC cân tại A;

D. A và B đều đúng.

3. Nhiều lựa chọn

Cho hai điểm D và E nằm trên đường trung trực của đoạn thẳng AB. Cho = 20°. Số đo $\hat{D B E}$ bằng :

A. 20°;

B. 30°;

C. 40°;

D. 10°.

4. Nhiều lựa chọn

Cho ∆ABC có E và D lần lượt là trung điểm của AB và BC. Từ E và D kẻ đường trung trực cắt nhau tại O. Cho F là trung điểm của AC. Khi đó:

A.OF là đường trung tuyến;

B. OF là đường trung trực của AC;

C. O là trực tâm của ∆ABC;

D. B và C đều đúng.

5. Nhiều lựa chọn

Trong khu dân cư có ba điểm dân cư D, E, F người ta muốn xây một công viên H cách đều cả ba điểm dân cư (như hình vẽ).

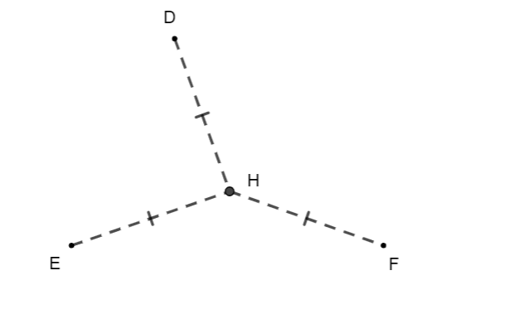
Trong khu dân cư có ba điểm dân cư D, E, F người ta muốn xây một công viên H cách (ảnh 1)

Khi đó vị trí của H là:

A. Trung điểm của EF;

B.Trọng tâm của ∆DEF;

C. Giao của ba đường trung trực của ∆DEF;

D.A và C đều đúng.

6. Nhiều lựa chọn

Cho tam giác ABC có E, F lần lượt là trung điểm của AB và BC. Cho O cách đều ba đỉnh của tam giác ABC. Khi đó:

A. OE vuông góc với AC;

B. OE vuông góc với AB;

C. OF vuông góc với AC;

D. OF vuông góc với AB.

7. Nhiều lựa chọn

Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{A G}{A M}$ bằng:

A. 2;

B. $\frac{1}{3}$

C. $\frac{3}{4}$

D. $\frac{1}{2}$

8. Nhiều lựa chọn

Cho tam giác ∆ABC cân tại A có hai đường trung tuyến BH và CK cắt nhau tại G. Biết BG = 6 cm. Độ dài đoạn thẳng CK bằng:

A. 9 cm;

B. 10 cm;

C. 12 cm;

D. 8 cm.

9. Nhiều lựa chọn

Cho tam giác ABC có hai đường trung tuyến AD và CE cắt nhau tại G. Đường thẳng BG cắt AC tại F. Cho AC = 10 cm. Độ dài đoạn thẳng AF bằng:

A. 10 cm;

B. 4 cm;

C. 5 cm;

D. 8 cm.

10. Nhiều lựa chọn

Cho tam giác DEF vuông tại E. Trên tia DE lấy điểm M sao sao DM = DF. Tia phân giác của góc $\hat{D}$ cắt EF tại H . Khi đó:

A. MH vuông góc với EF;

B. MH vuông góc với DF;

C. H là trực tâm của ∆MDF;

D. B và C đều đúng.

11. Nhiều lựa chọn

Cho tam giác ABC có đường cao BE và trực tâm K. Gọi H là giao điểm của AK và BC. Từ C kẻ đường thẳng vuông góc với BC cắt AB tại D. Khẳng định nào sau đây là đúng?

A. CD // AH;

B. CD // AB;

C.CD // BE;

D. CD $⊥$ BE;

12. Nhiều lựa chọn

Cho hình vẽ như bên dưới.Biết AH = 6 cm, BC = 8cm.

Cho hình vẽ như bên dưới. Biết AH = 6 cm, BC = 8 cm. Diện tích tam giác ABC bằng: (ảnh 1)

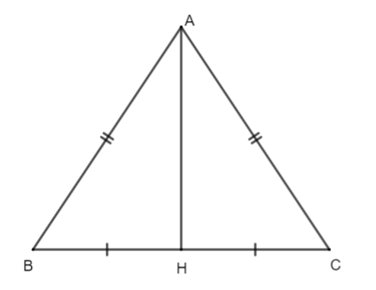
Diện tích tam giác ABC bằng:

A. 28 cm²;

B. 26 cm²;

C. 34 cm²;

D. 30 cm².

13. Nhiều lựa chọn

Cho ∆ABC cân tại A có hai đường phân giác từ góc B và góc C cắt nhau tại G. Cho góc $\hat{B A C}$ = 40°. Số đo $\hat{B G C}$ bằng:

A. 60°;

B. 90°;

C. 110°;

D. 120°.

14. Nhiều lựa chọn

Cho ∆ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Khẳng định nào sau đây là đúng?

A. Ba điểm A, G, I thẳng hàng;

B. Điểm G nằm trên đường phân giác của góc B;

C. Điểm G cách đều ba đỉnh của ∆ABC;

D. Điểm G cách đều ba cạnh của ∆ABC.

15. Nhiều lựa chọn

Một hòn đảo bị chia cắt bởi đường bờ biển tạo thành một hình tam giác. Các đường bờ biển được kí hiệu là các đường m,n,p(như hình vẽ). Người ta đặt một ngọn hải đăng trên hòn đảo để quan sát xung quanh. Vị trí của hải đăng để khoảng cách từ đó đến 3 đường bờ biển bằng nhau là:

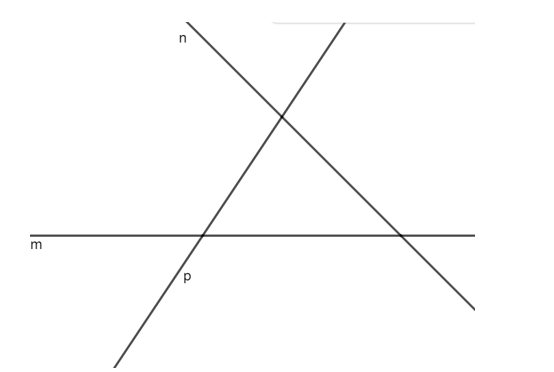
Một hòn đảo bị chia cắt bởi đường bờ biển tạo thành một hình tam giác. (ảnh 1)

A. Giao điểm ba đường trung tuyến của tam giác;

B. Giao điểm ba đường trung trực của tam giác;

C. Giao điểm ba đường cao của tam giác;

D. Giao điểm ba đường phân giác của tam giác.

16. Nhiều lựa chọn

Cho tam giác MNP có số đo như hình vẽ:

Cho tam giác MNP có số đo như hình vẽ: Có bao nhiêu khẳng định đúng trong các (ảnh 1)

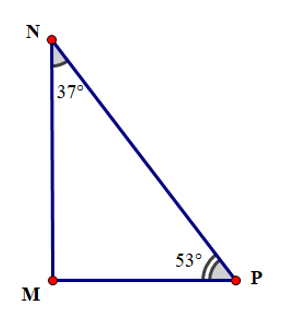
Có bao nhiêu khẳng định đúng trong các khẳng định sau:

(I). $\hat{M}$ = 80°.

(II). Tam giác MNP là tam giác nhọn.

(III). Tam giác MNP là tam giác vuông.

(IV). NP là cạnh huyền của tam giác MNP.

A. 1

B. 2

C. 3

D. 4

17. Nhiều lựa chọn

Tính số đo x trong hình sau:

Tính số đo x trong hình sau: A. 38độ ; B. 52 độ; C. 36 độ; D. 62 độ. (ảnh 1)

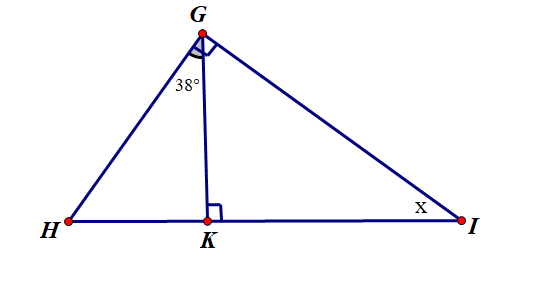
A. 38°;

B. 52°;

C. 36°;

D. 62°.

18. Nhiều lựa chọn

Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

A. 2 cm; 3 cm; 6 cm;

B. 3 cm; 6 cm; 3 cm;

C. 3 cm; 4 cm; 5 cm;

D. 5 cm; 6 cm; 7 dm.

19. Nhiều lựa chọn

Cho tam giác ABC có AB = 2, BC = 8 cm. Biết độ dài cạnh AC là một số nguyên tố. Chu vi tam giác ABC là:

A. 18 cm;

B. 7 cm;

C. 17 cm;

D. 19 cm.

20. Nhiều lựa chọn

Cho ∆ABC = ∆MNP. Biết AB = 7 cm, MP = 10 cm và chu vi của tam giác 24 cm. Tính các cạnh còn lại của mỗi tam giác.

A. MN = AC = 7 cm; BC = NP = 10 cm;

B. MN = AC = 10 cm; BC = NP = 7 cm;

C. MN = 7 cm; AC = 10 cm; BC = NP = 7 cm;

D. MN = 10 cm; AC = 7 cm; BC = NP = 7 cm.

21. Nhiều lựa chọn

Tính số đo x trên hình vẽ sau:

Tính số đo x trên hình vẽ sau: (ảnh 1)

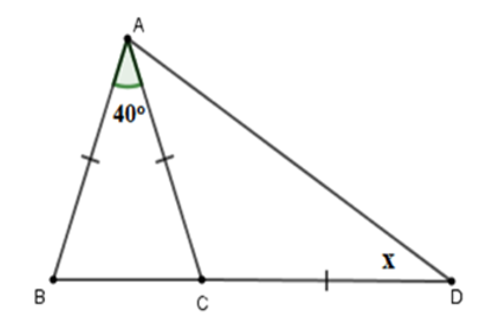
A. x = 45°;

B. x = 40°;

C. x = 35°;

D. x = 70°.

22. Nhiều lựa chọn

Cho tam giác ABC cân tại A có $\hat{A}$ = 2α. Tính số đo góc B theo α.

A. $\hat{B}$ = 90° + α;

B. $\hat{B} = \frac{180 ° - α}{2}$ ;

C. $\hat{B}$ = 180° − α;

D. $\hat{B}$ = 90° − α.

23. Nhiều lựa chọn

Cho ∆ABC $\hat{A} + \hat{B}$ = ∆DEF. Biết $\hat{E}$ = 130°, = 55°. Tính $\hat{A}, \hat{C}, \hat{D}, \hat{F}$ .

A. $\hat{A} = \hat{D}$ = 65°, $\hat{F} = \hat{C}$ = 50°;

B. $\hat{A} = \hat{D}$ = 50°, $\hat{F} = \hat{C}$ = 65°;

C. $\hat{A} = \hat{D}$ = 75°, $\hat{F} = \hat{C}$ = 50°;

D. $\hat{A} = \hat{D}$ = 50°, $\hat{F} = \hat{C}$ = 75°.

24. Nhiều lựa chọn

Trong tam giác ABC có AH vuông góc với BC (H $\in$ BC). Chọn câu sai.

A. Nếu AB < AC thì BH < HC;

B. Nếu AB > AC thì BH < HC;

C. Nếu AB = AC thì BH = HC;

D. Nếu BH > HC thì AB > AC.

25. Nhiều lựa chọn

Quan sát hình bên dưới. Có các đường xiên và đường vuông góc kẻ từ O xuống đường thẳng c, trong số các đường này đường nào ngắn nhất?

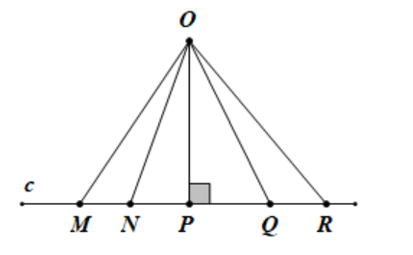
Quan sát hình bên dưới. Có các đường xiên và đường vuông góc kẻ từ O xuống đường (ảnh 1)

A. ON;

B. OM;

C. OP;

D. OR.

26. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có $\hat{A B C}$ = 60°, H là trung điểm của BC. Từ H kẻ đường vuông góc với BC cắt AC tại K. Tính $\hat{K B H}$ .

A. 30°;

B. 45°;

C. 60°;

D. 90°.

27. Nhiều lựa chọn

Cho tam giác ∆ABC có $\hat{A}$ là góc tù. Các đường trung trực của AB và AC cắt nhau tại O. Đường tròn tâm O bán kính OA đi qua điểm:

A. B và C;

B. M và N;

C. B;

D. C

28. Nhiều lựa chọn

Cho tam giác ∆ABC có M và N lần lượt là trung điểm của AB, BC. Từ M và N vẽ 2 đường trung trực cắt nhau tại O. Biết đường tròn tâm O bán kính OA có đường kính bằng 8 cm. Độ dài đoạn thẳng OB bằng:

A. 2 cm;

B. 4 cm;

C. 8 cm;

D. 5 cm.

29. Nhiều lựa chọn

Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:

A.Tam giác vuông;

B. Tam giác vuông cân;

C.Tam giác thường;

D.Tam giác cân.

30. Nhiều lựa chọn

Cho hình vẽ như bên dưới. Biết đường kính của đường tròn nằm trong tam giác là 8 cm. Độ dài của GK bằng:

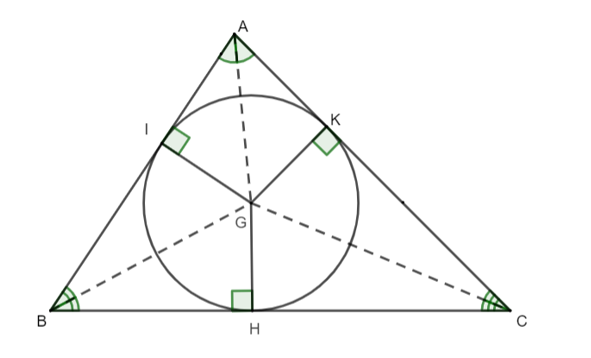
Cho hình vẽ như bên dưới. Biết đường kính của đường tròn nằm trong tam giác là 8 cm. (ảnh 1)

A. 8 cm;

B. 2 cm;

C. 4 cm;

D. 5 cm.

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi2 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi4 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi27 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi15 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi12 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi12 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi12 lượt thi

Facebook Youtube