30 CÂU HỎI
Cho hình vẽ. Tính góc FEC, biết EF // DC và \[\widehat {ECB} = 60^\circ \]:
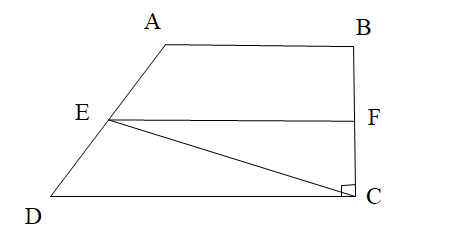
A. 50°;
B. 40°;
C. 60°;
D. 30°.
Cho hình bình hành ABCD như hình vẽ.
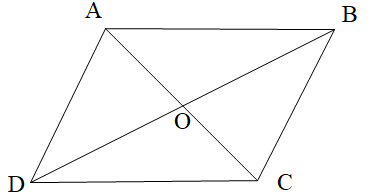
Chọn phương án đúng.
A. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù;
B. \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong;
C. \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị;
D. \[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh.
Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và \[\widehat {JOC} = 34^\circ \].
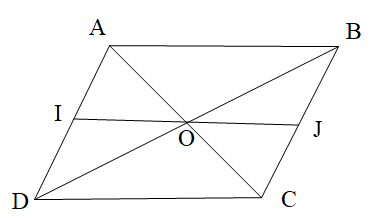
Số đo góc OCD là:
A. 60°;
B. 34°;
C. 40°;
D. 84°.
Cho hình thang ABCD như hình vẽ. Biết MN // DC, \[\widehat {DAB} = 120^\circ \] và \[\widehat {ANM} = 40^\circ \]. Số đo góc AHD là:
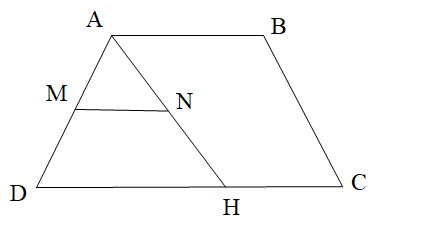
A. 60°;
B. 40°;
C. 30°;
D. 125°.
Cho hình vẽ dưới đây, biết a // b. Tính x, y.
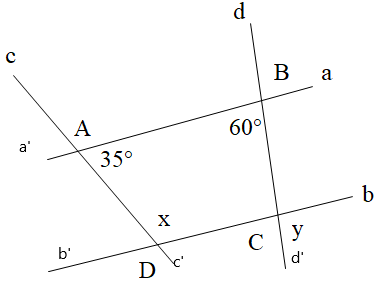
A. x = 60° và y = 35°;
B. x = 120° và y = 145°;
C. x = 35° và y = 60°;
D. x = 145° và y = 120°.
Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 124^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
A. 152°;
B. 143°;
C. 45°;
D. 35°.
Cho góc MON và OI tia phân giác của góc đó. Vẽ tia phân giác OJ của góc NOI. Biết \[\widehat {IOJ} = 39^\circ \]. Số đo góc MON là:
A. 145°;
B. 80°;
C. 156°;
D. 134°.
Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” và hình vẽ.
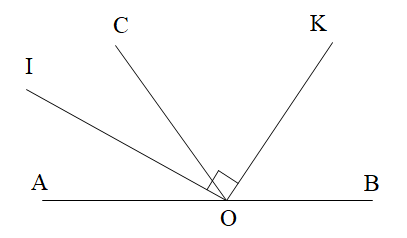
Kết luận của định lí là:
A. Kết luận: \[OI \bot OK\].
B. Kết luận: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOK, OK là tia phân giác AOI.
C. Kết luận: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOK.
D. Kết luận: \[OB \bot OK\].
Khi chứng minh định lí, người ta cần:
A. Chứng minh định lí đó đúng;
B. Chứng minh định lí đó đúng trong trường hợp cụ thể của giả thiết;
C. Chứng minh định lí đó đúng trong mọi trường hợp có thể xảy ra của giả thiết;
D. Chứng minh định lí đó đúng trong một vài trường hợp cụ thể của giả thiết.
Cho các phát biểu sau:
(1) Tổng số đo hai góc kề nhau bằng 180o;
(2) Hai góc bằng nhau thì đối đỉnh;
(3) Hai đường thẳng song song thì cắt nhau;
(4) Hai góc kề bù có tổng số đo bằng 180o;
(5) Nếu NH = NK thì N là trung điểm của HK.
Có bao nhiêu phát biểu đúng?
A. 1;
B. 2;
C. 3;
D. 5.
Cho hình vẽ.
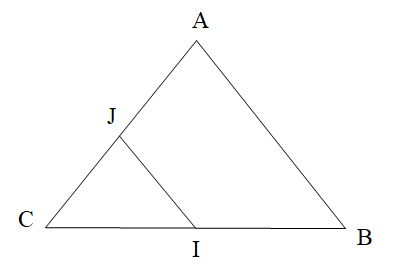
Góc CIJ và góc JIB là:
A. hai góc đối đỉnh;
B. hai góc đồng vị;
C. hai góc kề bù;
D. hai góc so le trong.
Trong các hình dưới đây hình nào chứa hai góc đối đỉnh.
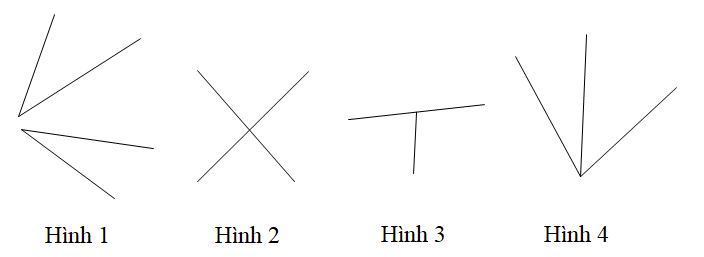
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Hình nào dưới đây vẽ Oz là tia phân giác của góc aOb.
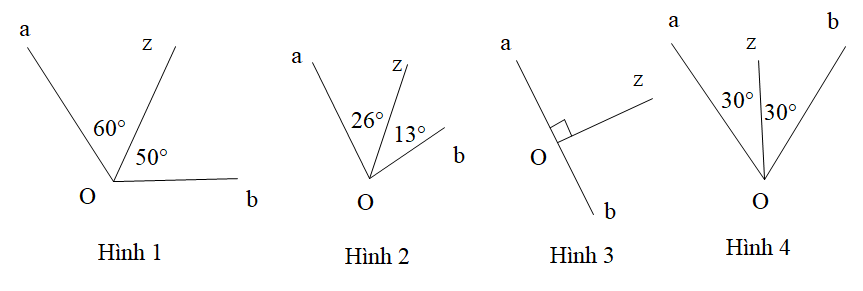
A. Hình 1, Hình 3;
B. Hình 2, Hình 4;
C. Hình 3, Hình 4;
D. Hình 4, Hình 1.
Hai đường thẳng mn và m’n’ cắt nhau tại điểm O. Góc đối đỉnh của \[\widehat {mOn'}\] là:
A. \[\widehat {m'On'}\]
B. \[\widehat {m'On}\]
C. \[\widehat {mOn'}\]
D. \[\widehat {mOn}\]
Cho ba đường thẳng phân biệt a, b và c, biết c // a và c // b. Kết luận nào đúng:
A. a // b;
B. \[b \bot c\];
C. \[a \bot b\];
D. Cả 3 đáp án đều sai.
Tìm số đo x:
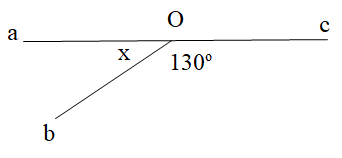
A. 65°;
B. 120°;
C. 95°;
D. 50°.
Cho hình vẽ như bên dưới. Tính \[\widehat {{N_3}}\], biết a // b và \[\widehat {{M_1}} = 50^\circ \].
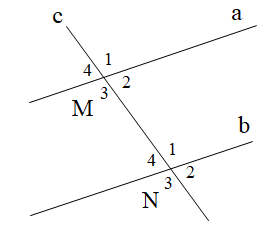
A. 50o;
B. 60o;
C. 65o;
D. 85o.
Cho hai điểm phân biệt H, K. Ta vẽ một đường thẳng x đi qua điểm H và một đường thẳng y đi qua điểm K sao cho x // y. Có thể vẽ được bao nhiêu cặp đường thẳng x, y thỏa mãn điều kiện trên.
A. Ba cặp;
B. Bốn cặp;
C. Một cặp;
D. Vô số cặp.
Biết một cặp góc so le trong \[\widehat {{A_4}}\; = \widehat {{B_2}} = 110^\circ \]. Tính số đo của cặp góc so le trong còn lại:
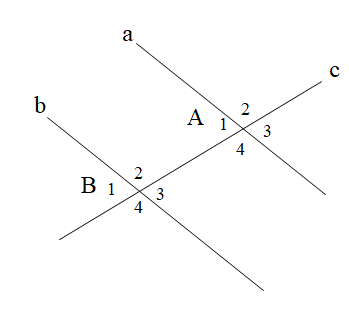
A. 149°;
B. 136°;
C. 70°;
D. 64°.
Cho hình vẽ
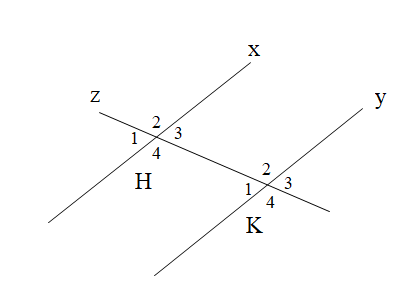
Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].
A. 180°;
B. 141°;
C. 120°;
D. 138°.
Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
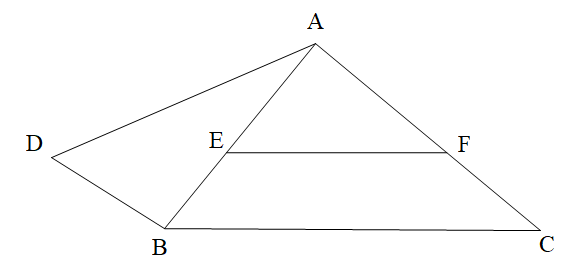
A. \[\widehat {DAB}\] và \[\widehat {EAD}\] là hai góc so le trong;
B. \[\widehat {AFE}\] và \[\widehat {BAC}\] là hai góc so le trong;
C. \[\widehat {AFE}\] và \[\widehat {ACB}\] là hai góc đồng vị;
D. \[\widehat {BAC}\] và \[\widehat {DAB}\] là hai góc đồng vị.
Cho hình vẽ
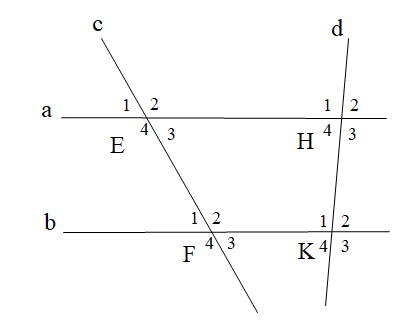
Biết a // b,
\[{\widehat E_1} = 48^\circ \]. Số đo \[\widehat {{F_3}}\] là:
A. 51°;
B. 129°;
C. 138°;
D. 48°.
Cho hình vẽ dưới đây, biết a // b. Tính x, y.

A. x = 60° và y = 35°;
B. x = 120° và y = 145°;
C. x = 35° và y = 60°;
D. x = 145° và y = 120°.
Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 124^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
A. 152°;
B. 143°;
C. 45°;
D. 35°.
Phát biểu định lí sau bằng lời.
|
Giả thiết |
t cắt m tại A, t cắt n tại B \[\widehat {{A_1}}\] và \[\widehat {{B_1}}\]là hai góc đồng vị \[\widehat {{A_1}} = \widehat {{B_1}}\] |
|
Kết luận |
m // n |
A. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n vuông góc với nhau;
B. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n song song với nhau;
C. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n song song với nhau;
D. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n vuông góc với nhau.
“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”
Hình minh họa nội dung định lí trên là
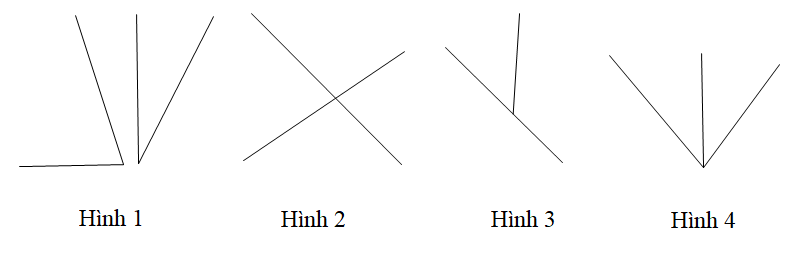
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Cho hình vẽ,
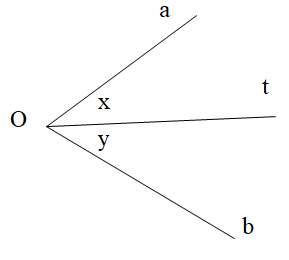
Biết \[\widehat {aOb} = 70^\circ \] và tia Ot là tia phân giác góc xOy. Tính x, y.
A. \[x = y = 35^\circ \];
B. \[x = 35^\circ ;y = 45^\circ \];
C. \[x = 45^\circ ;y = 35^\circ \];
D. \[x = y = 70^\circ \].
Chọn đáp án đúng.
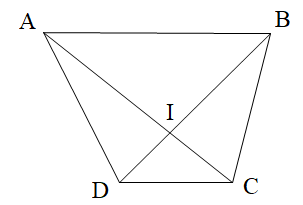
A. \[\widehat {AID}\]và \[\widehat {CIB}\] là hai góc kề bù;
B. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù;
C. \[\widehat {AIB}\] và \[\widehat {BIC}\] là hai góc kề bù;
D. \[\widehat {AIB}\] và \[\widehat {DIC}\] là hai góc kề bù.
Viết giả thiết, kết luận cho định lí sau:
“Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”
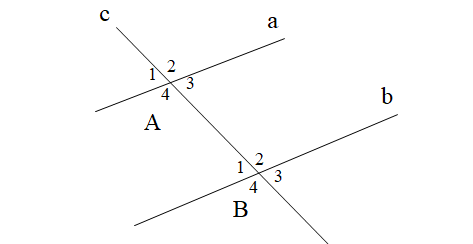
A.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_4}}\] và \[\widehat {{B_2}}\] là hai góc so le trong \[\widehat {{A_4}} = \widehat {{B_2}}\] |
|
Kết luận |
a // b |
B.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đối đỉnh \[\widehat {{A_3}} = \widehat {{B_1}}\] |
|
Kết luận |
a // b |
C.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
|
Kết luận |
a // b |
D.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
|
Kết luận |
a // b |
Điền vào chỗ trống nội dung phù hợp.
Nếu góc xOt và góc tOy là hai góc kề bù thì tổng số đo hai góc bằng 180o.
![]()
![]()
Giả thiết ...........
A. kết luận;
B. khẳng định;
C. chứng minh;
D. Cả 3 đáp án đều đúng.


