Quiz

50 câu Trắc nghiệm Toán 9 Bài 2: Tỉ số lượng giác của góc nhọn có đáp án (Phần 2)

Admin50 câu hỏiToánLớp 9

Bắt đầu ngay

50 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho tam giác MNP vuông tại M. Khi đó cos $\hat{M N P}$ bằng:

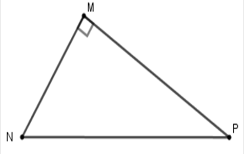
Cho tam giác MNP vuông tại M. Khi đó cosMNP bằng A. MN/NP B. MP/ NP C. MN/ MP (ảnh 1)

A. $\frac{M N}{N P}$

B. $\frac{M P}{N P}$

C. $\frac{M N}{M P}$

D. $\frac{M P}{M N}$

2. Nhiều lựa chọn

Cho tam giác MNP vuông tại M. Khi đó tan $\hat{M N P}$ bằng:

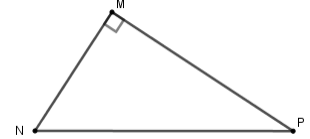
Cho tam giác MNP vuông tại M. Khi đó tanMNP bằng: A. MN/ NP B. MP/ NP C. MN/ MP (ảnh 1)

A. $\frac{M N}{N P}$

B. $\frac{M P}{N P}$

C. $\frac{M N}{M P}$

D. $\frac{M P}{M N}$

3. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Chọn khẳng định đúng.

A. sin $α$ + cos $α$ = 1

B. sin² $α$ + cos² $α$ = 1

C. sin³ $α$ + cos³ $α$ = 1

D. sin $α$ − cos $α$ = 1

4. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Chọn khẳng định sai:

A. $\tan α = \frac{\sin α}{\cos α}$

B. $\cot α = \frac{\cos α}{\sin α}$

C. tan $α$ .cot $α$ = 1

D. tan² $α$ − 1 = cos² $α$

5. Nhiều lựa chọn

Cho $α$ và $β$ là hai góc nhọn bất kì thỏa mãn $α + β = 90^{0}$ . Khẳng định nào sau đây là đúng?

A. tan $α$ = sin $α$

B. tan $α$ = cot $α$

C. tan $α$ = cos $α$

D. tan $α$ = tan $α$

6. Nhiều lựa chọn

Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì:

A. sin góc nọ bằng cosin góc kia.

B. sin hai góc bằng nhau

C. tan góc nọ bằng cotan góc kia

D. Cả A và C đều đúng.

7. Nhiều lựa chọn

Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác sinB và cosB.

A. sin B = 0,6; cos B = 0,8

B. sin B = 0,8; cos B = 0,6

C. sin B = 0,4; cos B = 0,8

D. sin B = 0,6; cos B = 0,4

8. Nhiều lựa chọn

Cho tam giác vuông ABC vuông tại C có AC = 1cm, BC = 2cm. Tinh các tỉ số lượng giác sin B, cos B

A. sin B = $\frac{1}{\sqrt{3}}$ ; cos B = $\frac{2 \sqrt{3}}{3}$

B. sin B = $\frac{\sqrt{5}}{5}$ ; cos B = $\frac{2 \sqrt{5}}{5}$

C. sin B = $\frac{1}{2}$ ; cos B = $\frac{2}{\sqrt{5}}$

D. sin B = $\frac{2 \sqrt{5}}{5}$ ; cos B = $\frac{\sqrt{5}}{5}$

9. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AC = 3; AB = 4. Khi đó cosB bằng:

A. $\frac{3}{4}$

B. $\frac{3}{5}$

C. $\frac{4}{3}$

D. $\frac{4}{5}$

10. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC. (làm tròn đến chữ số thập phân thứ 2)

A. tan C $\approx$ 0,87

B. tan C $\approx$ 0,86

C. tan C $\approx$ 0,88

D. tan C $\approx$ 0,89

11. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = 9cm; AC = 5cm. Tính tỉ số lượng giác tan C (làm tròn đến chữ số thập phân thứ 1)

A. tan C $\approx$ 0,67

B. tan C $\approx$ 0,5

C. tan C $\approx$ 1,4

D. tan C $\approx$ 1,5

12. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, đường cao AH có AB = 13cm, BH = 0,5dm. Tính tỉ số lượng giác sinC (làm tròn đến chữ số thập phân thứ 2)

A. sin C $\approx$ 0,35

B. sin C $\approx$ 0,37

C. sin C $\approx$ 0,39

D. sin C $\approx$ 0,38

13. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, đường cao AH có AC = 15cm, CH = 6cm. Tính tỉ số lượng giác cos B.

A. cos B = $\frac{5}{\sqrt{21}}$

B. cos B = $\frac{\sqrt{21}}{5}$

C. cos B = $\frac{3}{5}$

D. cos B = $\frac{2}{5}$

14. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, $\hat{A B C} = 60^{0}$ , cạnh AB = 5cm. Độ dài cạnh AC là:

A. 10cm

B. $\frac{5 \sqrt{3}}{2}$ cm

C. 5 $\sqrt{3}$ cm

D. $\frac{5}{\sqrt{3}}$ cm

15. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, đường cao AH có CH = 4cm, BH = 3cm. Tính tỉ số lượng giác cos C (làm tròn đến chữ số thập phân thứ 2)

A. cos C $\approx$ 0,76

B. cos C $\approx$ 0,77

C. cos C $\approx$ 0,75

D. cos C $\approx$ 0,78

16. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, đường cao AH có CH = 11cm, BH = 12cm. Tính tỉ số lượng giác cos C (làm tròn đến chữ số thập phân thứ 2)

A. cos C $\approx$ 0,79

B. cos C $\approx$ 0,69

C. cos C $\approx$ 0,96

D. cos C $\approx$ 0,66

17. Nhiều lựa chọn

Cho tam giác ABC vuông tại A. Hãy tính tanC biêt rằng cotB = 2

A. tanC = $\frac{1}{4}$

B. tanC = 4

C. tanC = 2

D. tanC = $\frac{1}{2}$

18. Nhiều lựa chọn

Cho tam giác ABC vuông tại A. Hãy tính tan C biết rằng tan B = 4

A. tan C = $\frac{1}{4}$

B. tan C = 4

C. tan C = 2

D. tan C = $\frac{1}{2}$

19. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AB = 5cm, cot C = $\frac{7}{8}$ . Tính độ dài các đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ 2)

A. AC $\approx$ 4,39 (cm); BC $\approx$ 6,66 (cm)

B. AC $\approx$ 4,38 (cm); BC $\approx$ 6,65 (cm)

C. AC $\approx$ 4,38 (cm); BC $\approx$ 6,64 (cm)

D. AC $\approx$ 4,37 (cm); BC $\approx$ 6,67 (cm)

20. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AB = 9cm, tan C = $\frac{5}{4}$ . Tính độ dài cac đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ hai)

A. AC = 11,53; BC = 7,2

B. AC = 7; BC $\approx$ 11,53

C. AC = 5,2; BC $\approx$ 11

D. AC = 7,2; BC $\approx$ 11,53

21. Nhiều lựa chọn

Cho $α$ là góc nhọn, tính sin $α$ , cot $α$ biết cos $α$ = $\frac{2}{5}$

A. sin $α$ = $\frac{\sqrt{21}}{25}$ ; cot $α$ = $\frac{3 \sqrt{21}}{21}$

B. sin $α$ = $\frac{\sqrt{21}}{5}$ ; cot $α$ = $\frac{5}{\sqrt{21}}$

C. sin $α$ = $\frac{\sqrt{21}}{3}$ ; cot $α$ = $\frac{3}{\sqrt{21}}$

D. sin $α$ = $\frac{\sqrt{21}}{5}$ ; cot $α$ = $\frac{2}{\sqrt{21}}$

22. Nhiều lựa chọn

Tính sin $α$ , tan $α$ biết cos $α$ = $\frac{3}{4}$

A. sin $α$ = $\frac{4}{\sqrt{7}}$ ; tan $α$ = $\frac{\sqrt{7}}{3}$

B. sin $α$ = $\frac{\sqrt{7}}{4}$ ; tan $α$ = $\frac{3}{\sqrt{7}}$

C. sin $α$ = $\frac{\sqrt{7}}{4}$ ; tan $α$ = $\frac{\sqrt{7}}{3}$

D. sin $α$ = $\frac{\sqrt{7}}{3}$ ; tan $α$ = $\frac{\sqrt{7}}{4}$

23. Nhiều lựa chọn

Không dùng bảng số và máy tính, hãy so sánh $\sin 20^{0}$ và $\sin 70^{0}$

A. $\sin 20^{0}$ < $\sin 70^{0}$

B. $\sin 20^{0}$ > $\sin 70^{0}$

C. $\sin 20^{0}$ = $\sin 70^{0}$

D. $\sin 20^{0} \geq \sin 70^{0}$

24. Nhiều lựa chọn

Không dùng bảng số và máy tính, hãy so sánh $c o t 50^{0}$ và $c o t 46^{0}$

A. $c o t 46^{0} = c o t 50^{0}$

B. $c o t 46^{0} > c o t 50^{0}$

C. $c o t 46^{0} < c o t 50^{0}$

D. $c o t 46^{0} \geq c o t 50^{0}$

25. Nhiều lựa chọn

Sắp xếp các tỉ số lượng giác $\tan 43^{0}$ , $c o t 71^{0}$ , $\tan 38^{0}$ , $c o t 69^{0} 15'$ , $\tan 28^{0}$ theo thứ tự tăng dần.

A. $c o t 71^{0}$ < $c o t 69^{0} 15'$ < $\tan 28^{0}$ < $\tan 38^{0}$ < $\tan 43^{0}$

B. $c o t 69^{0} 15'$ < $c o t 71^{0}$ < $\tan 28^{0}$ < $\tan 38^{0}$ < $\tan 43^{0}$

C. $\tan 28^{0}$ < $\tan 38^{0}$ < $\tan 43^{0}$ < $c o t 69^{0} 15'$ < $c o t 71^{0}$

26. Nhiều lựa chọn

Sắp xếp các tỉ số lượng giác $\sin 40^{0}$ , $c o s 67^{0}$ , $\sin 35^{0}$ , $c o s 44^{0} 35'$ ; $\sin 28^{0} 10'$ theo thứ tự tăng dần.

A. $c o s 67^{0}$ < $\sin 35^{0}$ < $\sin 28^{0} 10'$ < $\sin 40^{0}$ < $c o s 44^{0} 35'$

B. $c o s 67^{0}$ < $c o s 44^{0} 35'$ < $\sin 40^{0}$ < $\sin 28^{0} 10'$ < $\sin 35^{0}$

C. $c o s 67^{0}$ > $\sin 28^{0} 10'$ > $\sin 35^{0}$ > $\sin 40^{0}$ > $c o s 44^{0} 35'$

27. Nhiều lựa chọn

Tính giá trị biểu thức A = $\sin^{2} 1^{0}$ + $\sin^{2} 2^{0}$ + … + $\sin^{2} 88^{0}$ + $\sin^{2} 89^{0}$ + $\sin^{2} 90^{0}$

A. A = 46

B. A = $\frac{93}{2}$

C. A = $\frac{91}{2}$

D. A = 45

28. Nhiều lựa chọn

Tính giá trị biểu thức $\sin^{2} 10^{0}$ + $\sin^{2} 20^{0}$ + … + $\sin^{2} 70^{0}$ + $\sin^{2} 80^{0}$

A. 0

B. 8

C. 5

D. 4

29. Nhiều lựa chọn

Giá trị của biểu thức P = $\cos^{2} 20^{0}$ + $\cos^{2} 40^{0}$ + $\cos^{2} 50^{0}$ + $\cos^{2} 70^{0}$

A. 0

B. 1

C. 2

D. 3

30. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Khi đó C = sin⁴ $α$ + cos⁴ $α$ bằng:

A. C = $1 - 2 \sin^{2} α . c o s^{2}$

B. C = 1

C. C = $\sin^{2} α . c o s^{2}$ $α$

D. C = $1 + 2 \sin^{2} α . c o s^{2}$ $α$

31. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Khi đó $C = \sin^{6} α + \cos^{6} α + 3 \sin^{2} α . \cos^{2} α$ bằng:

A. C = $1 - 3 \sin^{2} α . \cos^{2} α$

B. C = 1

C. C = $\sin^{2} α . \cos^{2} α$

D. C = $3 \sin^{2} α . \cos^{2} α - 1$

32. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Rút gọn $P = (1 - \sin^{2} α) . c o t^{2} α + 1 - c o t^{2} α$ ta được:

A. P = $\sin^{2} α$

B. P = $\cos^{2} α$

C. P = $\tan^{2} α$

D. P = 2 $\sin^{2} α$

33. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Cho $P = (1 - \sin^{2} α) . \tan^{2} α + (1 - \cos^{2} α) co t^{2} α$ , chọn kết luận đúng.

A. P > 1

B. P < 1

C. P = 1

D. P = $2 \sin^{2} α$

34. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Biểu thức $Q = \frac{1 + \sin^{2} α}{1 - \sin^{2} α}$ bằng:

A. Q = $1 + \tan^{2} α$

B. Q = $1 + 2 \tan^{2} α$

C. Q= $1 - \tan^{2} α$

D. Q = $2 \tan^{2} α$

35. Nhiều lựa chọn

Cho $α$ là góc nhọn bất kỳ. Biểu thức $Q = \frac{\cos^{2} α - \sin^{2} α}{c o s α . \sin α}$ bằng:

A. Q = cot $α$ − tan $α$

B. Q = cot $α$ + tan $α$

C. Q = tan $α$ − cot $α$

D. Q = 2 tan $α$

36. Nhiều lựa chọn

Cho tan $α$ = 2. Tính giá trị của biểu thức: $G = \frac{2 \sin α + \cos α}{\cos α - 3 \sin α}$

A. G = 1

B. G = $- \frac{4}{5}$

C. G = $- \frac{6}{5}$

D. G = −1

37. Nhiều lựa chọn

Cho tan $α$ = 4. Tính giá trị của biểu thức $P = \frac{3 \sin α - 5 \cos α}{4 \cos α + \sin α}$

A. P = $\frac{7}{8}$

B. P = $\frac{17}{8}$

C. P = $\frac{8}{7}$

D. P = $\frac{5}{8}$

38. Nhiều lựa chọn

Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2. Khi đó $\tan \hat{A B C} . \tan \hat{A C B}$ bằng?

A. 2

B. 3

C. 1

D. 4

39. Nhiều lựa chọn

Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 3:2. Khi đó $\tan \hat{A B C} . \tan \hat{A C B}$ bằng?

A. 3

B. 5

C. $\frac{3}{5}$

D. $\frac{5}{3}$

40. Nhiều lựa chọn

Cho $α$ là góc nhọn. Tính $c o t α$ biết $\sin α = \frac{5}{13}$

A. cot $α$ = $\frac{12}{5}$

B. cot $α$ = $\frac{11}{5}$

C. cot $α$ = $\frac{5}{12}$

D. cot $α$ = $\frac{13}{5}$

41. Nhiều lựa chọn

Tính các giá trị lượng giác còn lại của góc $α$ biết $\sin α = \frac{3}{5}$

A. $\cos α = \frac{3}{4}$ ; $\tan α = \frac{3}{4}$ ; $c o t α = \frac{4}{5}$

B. $\cos α = \frac{4}{5}$ ; $\tan α = \frac{3}{4}$ ; $c o t α = \frac{4}{3}$

C. $\cos α = \frac{4}{5}$ ; $\tan α = \frac{3}{4}$ ; $c o t α = \frac{4}{5}$

B. $\cos α = \frac{3}{4}$ ; $\tan α = \frac{4}{5}$ ; $c o t α = \frac{4}{3}$

42. Nhiều lựa chọn

Tính giá trị biểu thức $B = \tan 1^{0} . \tan 2^{0} . \tan 3^{0} . . . \tan 88^{0} . \tan 89^{0}$

A. B = 44

B. B = 1

C. B = 45

D. B = 2

43. Nhiều lựa chọn

Tính giá trị biểu thức $B = \tan 10^{0} . \tan 20^{0} . . . \tan 80^{0}$

A. B = 44

B. B = 1

C. B = 45

D. B = 2

44. Nhiều lựa chọn

Chọn kết luận đúng về giá trị biểu thức $B = \frac{\cos^{2} α - 3 \sin^{2} α}{3 - \sin^{2} α}$ biết $\tan α = 3$

A. B > 0

B. B < 0

C. 0 < B < 1

D. B = 1

45. Nhiều lựa chọn

Cho tam giác ABC cân tại A có AB = AC = 13cm; BC = 10cm. Tính sin A

A. sin A = $\frac{120}{169}$

B. sin A = $\frac{60}{169}$

C. sin A = $\frac{5}{6}$

D. sin A = $\frac{10}{13}$

46. Nhiều lựa chọn

Tính diện tích hình bình hành ABCD biết AD = 12cm; DC = 15cm; $\hat{A D C} = 70^{0}$

A. 169,1 $c m^{2}$

B. 129,6 $c m^{2}$

C. 116,5 $c m^{2}$

D. 115,8 $c m^{2}$

47. Nhiều lựa chọn

Tính số đo góc nhọn $α$ biết $10 \sin^{2} α + 6 \cos^{2} = 8$

A. $α = 30^{0}$

B. $α = 45^{0}$

C. $α = 30^{0}$

D. $α = 120^{0}$

48. Nhiều lựa chọn

Tính giá trị của các biểu thức sau:

$A = \sin^{2} 15^{0} + \sin^{2} 25^{0} + \sin^{2} 35^{0} + \sin^{2} 45^{0} + \sin^{2} 55^{0} + \sin^{2} 65^{0} + \sin^{2} 75^{0}$

A. A = 0

B. A = $\frac{7}{2}$

C. A = − $\frac{7}{2}$

D. A = $\frac{5}{2}$

49. Nhiều lựa chọn

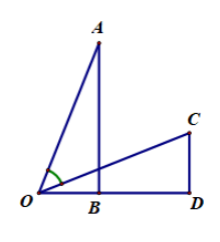
Cho hai tam giác vuông OAB và OCD như hình vẽ. Biết OB = CD = a, AB = OD = b. Tính $\cos \hat{A O C}$ theo a và b

Cho hai tam giác vuông OAB và OCD như hình vẽ. Biết OB = CD = a, AB = OD = b. (ảnh 1)

A. $\frac{2 a b}{a^{2} + b^{2}}$

B. $\frac{b^{2} - a^{2}}{a^{2} + b^{2}}$

C. 1

D. $\frac{a^{2} - b^{2}}{a^{2} + b^{2}}$

50. Nhiều lựa chọn

Biết $0^{0} < α < 90^{0}$ . Giá trị của biểu thức:

$[\sin α + 3 \cos (90^{0} - α)] : [\sin α - 2 \cos (90^{0} - α)]$ bằng:

A. −4

B. 4

C. $\frac{- 3}{2}$

D. $\frac{3}{2}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube