8 CÂU HỎI
Trong hệ tọa độ Oxy, cho ba điểm A(0; –3), B(2; 1), D(5; 5). Tìm tọa độ điểm C để tứ giác ABCD là hình bình hành.
A. C(3; 1);
B. C(–3; –1);
C. C(7; 9);
D. C(–7; –9).
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Khẳng định nào sau đây là sai?
A. \(\overrightarrow {BC'} = \overrightarrow {C'A} = \overrightarrow {A'B'} \);
B. \(\overrightarrow {B'C'} = \overrightarrow {A'B} = \overrightarrow {CA'} \);
C. \(\overrightarrow {C'A'} = \frac{1}{2}\overrightarrow {AC} \);
D. \(\overrightarrow {BA} + \overrightarrow {AB'} = \overrightarrow {AA'} \).
Một bồn nước inox có dạng một hình trụ có chiều cao 1,75 m và diện tích đáy là 0,32 m2. Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước).
A. 0,48 m3;
B. 0,54 m3;
C. 0,56 m3;
D. 0,6 m3.
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở giữa là 3 m x 6 m. Hãy tính khoảng cách giữa hai điểm A và B.
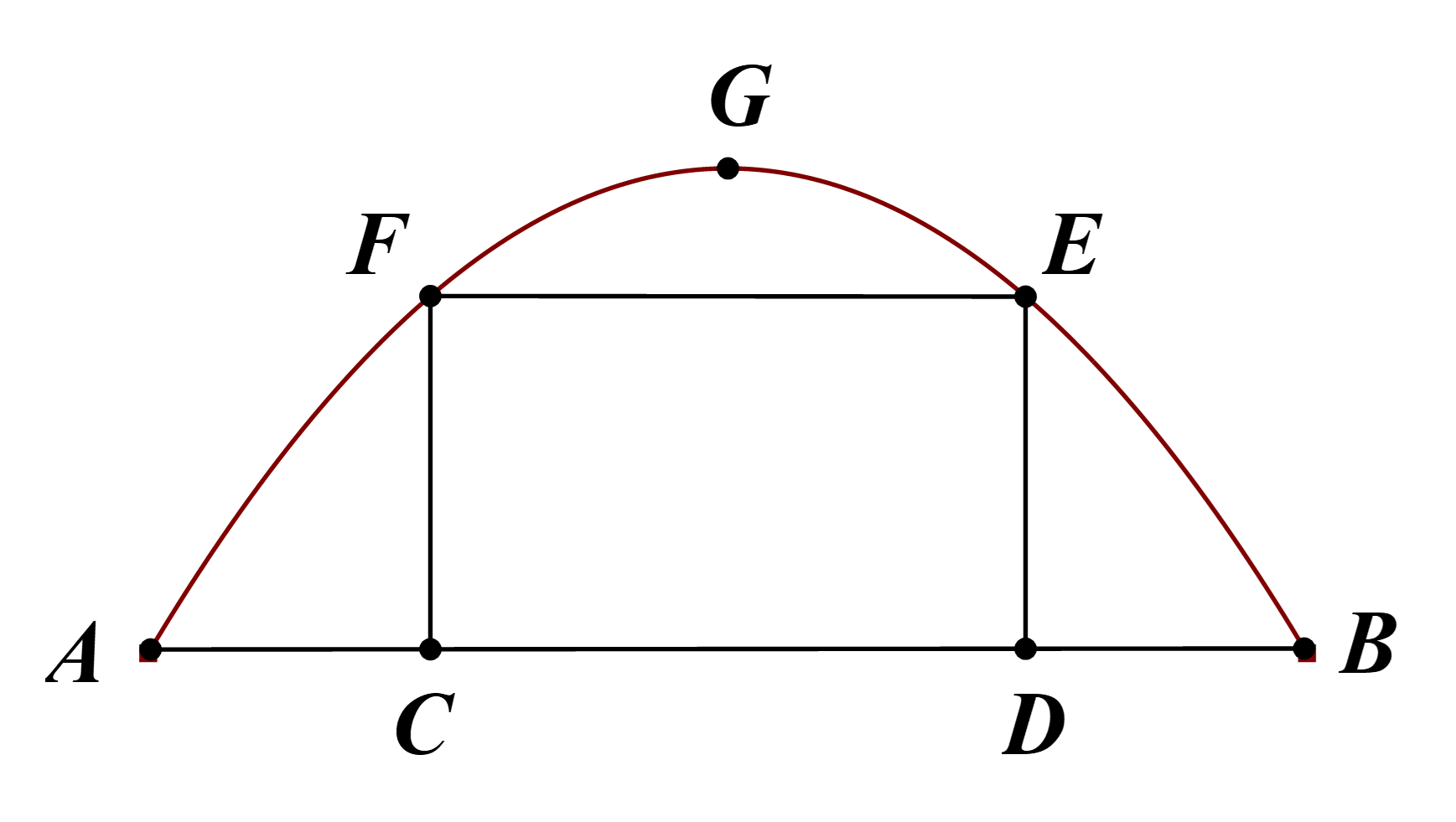
A. 13 m;
B. 14 m;
C. 12 m;
D. 10 m.
Cho hình vuông ABCD cạnh a. Tính độ dài vectơ \(\vec u = 4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \).
A. \(\left| {\vec u} \right| = a\sqrt 5 \);
B. \(\left| {\vec u} \right| = \frac{{a\sqrt 5 }}{2}\);
C. \(\left| {\vec u} \right| = 3a\sqrt 5 \);
D. \(\left| {\vec u} \right| = 2a\sqrt 5 \).
Cho hàm số y = f(x). Đồ thị của hàm số y = f’(x) như hình bên.
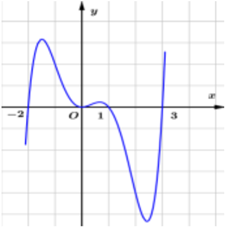
Hàm số g(x) = f(x2) có bao nhiêu điểm cực trị?
A. 4
B. 3
C. 5
D. 2
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, SA = SB = SD = a, \[\widehat {BAD} = 60^\circ \]. Góc giữa đường thẳng SA và mặt phẳng (SCD) bằng
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Cho tam giác ABC, với M, N, P lần lượt là trung điểm BC, CA, AB. Khẳng định nào sau đây sai?
A. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \vec 0\);
B. \(\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \vec 0\);
C. \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \vec 0\);
D. \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {MP} \).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải