8 CÂU HỎI
Một hộp đựng 7 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 8 viên bi có đủ 3 màu?
A. 12 201;
B. 10 224;
C. 12 422;
D. 14 204.
Với giá trị lớn nhất của a bằng bao nhiêu để phương trình: asin2x + 2sin2x + 3acos2x = 2 có nghiệm
A. 2;
B. \(\frac{{11}}{3}\);
C. 4;
D. \(\frac{8}{3}\).
Cho nửa hình tròn H như hình vẽ, đường kính hình tròn là 12cm.
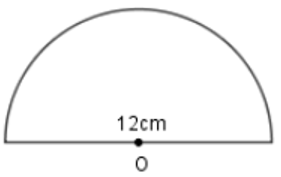
Chu vi hình H là:
A. 18,84 cm;
B. 30,84 cm;
C. 37,68 cm;
D. 49,68 cm.
Cho hai đường thẳng song song d1, d2. Trên đường thẳng d1 lấy 10 điểm phân biệt, trên đường thẳng d2 lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác tạo thành mà ba đỉnh của nó được chọn từ 25 điểm vừa nói ở trên?
A. \(C_{10}^2C_{15}^1\);
B. \(C_{10}^1C_{15}^2\);
C. \(C_{10}^2C_{15}^1 + C_{10}^1C_{15}^2\);
D. \(C_{10}^2C_{15}^1C_{10}^1C_{15}^2\).
Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
A. 1470;
B. 750;
C. 2940;
D. 1500.
Một tổ có 9 học sinh, trong đó có 5 học sinh nam và 4 học sinh nữ được xếp thành hàng dọc. Xác suất sao cho 5 học sinh nam đứng kề nhau là
A. \(\frac{5}{{126}}\);
B. \(\frac{{121}}{{126}}\);
C. \(\frac{1}{{126}}\);
D. \(\frac{6}{{125}}\).
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
A. 6;
B. 8;
C. 7;
D. 5.
Cho hình chữ nhật ABCD có AB = 4, AD = 3. Tính độ dài vectơ\(\overrightarrow {AB} + \overrightarrow {AD} \)
A. 12;
B. 5;
C. \(\sqrt 7 \);
D. 7.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải