10 CÂU HỎI
Cho tam giác ABC có AB = 5, BC = 6 và AC = 9. Gọi M là trung điểm của BC, N là điểm thuộc cạnh AC sao cho AC = 3NC. Tính tích vô hướng \(\overrightarrow {AM} .\overrightarrow {BN} \).
A. \(\frac{{26}}{3}\).
B. \(\frac{{11}}{3}\).
C. \(\frac{{35}}{3}\).
D. \(\frac{8}{3}\).
Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng d: y = mx – m + 1 (m ≠ 0) lớn nhất.
A. \(m = - 1 + \sqrt 2 \).
B. m = 2.
C. \(m = \sqrt 2 \).
D. m = –1.
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \sqrt {x - m} + \sqrt {2x - m - 1} \) xác định trên (0; +∞).
A. m ≤ 0.
B. m ≥ 1.
C. m ≤ 1.
D. m ≤ –1.
Cho hai tập hợp A = (m – 1; 5], B = (3; 2020 – 5m) và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để A \ B = ∅?
A. 3.
B. 399.
C. 398.
D. 2.
Hai người xài youtube mất 2 phút để đăng 2 đoạn video. Vậy cần bao nhiêu người để đăng được 18 clip trong vòng 6 phút?
A. 3.
B. 6.
C. 12.
Đồ thị hàm số y = –5x không đi qua điểm:
A. M(1; 5);
B. N(–2; 10);
C. P(–1; 5);
D. Q(2; –10).
Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.
A. \(\frac{{36}}{{285}}\).
B. \(\frac{{18}}{{285}}\).
C. \(\frac{{72}}{{285}}\).
D. \(\frac{{144}}{{285}}\).
Phương trình \({9^{{x^2} + x - 1}} - {10.3^{{x^2} + x - 2}} + 1 = 0\) có tập nghiệm là
A. {–2; –1; 1; 2}.
B. {–2; 0; 1; 2}.
C. {–2; –1; 0; 1}.
D. {–1; 0; 2}.
Cho hàm số y = ax2 + bx + c có đồ thị như hình vẽ bên.
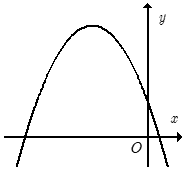
Khẳng định nào sau đây đúng?
A. a > 0, b < 0, c > 0.
B. a < 0, b < 0, c < 0.
C. a < 0, b > 0, c > 0.
D. a < 0, b < 0, c > 0.
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
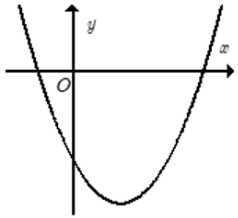
Khẳng định nào sau đây đúng?
A. a > 0, b < 0, c < 0.
B. a > 0, b < 0, c > 0.
C. a > 0, b > 0, c > 0.
D. a < 0, b < 0, c > 0.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải