41 CÂU HỎI
Gọi điểm M là điểm thuộc cạnh BC của tam giác ABC sao cho BM = 3MC. Khi đó \(\overrightarrow {AM} \) bằng
A. \(\frac{1}{2}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} \);
B. \(\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \);
C. \(\frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} \);
D. \(\frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \).
Cho a là số dương khác 1, b là số dương và c là số thực bất kì. Mệnh đề nào dưới đây là đúng?
A. \({\log _a}{b^c} = \frac{1}{c}{\log _a}b\);
B. logabc = clogab;
C. \({\log _{{a^c}}}b = c{\log _a}b\);
D. \({\log _{{a^c}}}b = c{\log _a}b\).
Tiếp tuyến tại điểm M(1; 3) cắt đồ thị hàm số y = x3 – x + 3 tại điểm thứ hai khác M là N. Tọa độ điểm N là:
A. N(−2; −3);
B. N(1; 3);
C. N(−1; 3);
D. M(2; 9).
Cho hình chóp S.ABC, gọi G là trọng tâm tam giác ABC. Tìm mệnh đề đúng trong các mệnh đề sau:
A. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 4\overrightarrow {SG} \);
B. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SG} \);
C. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 2\overrightarrow {SG} \);
D. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \).
Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị nhứ hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a, b, c, d.
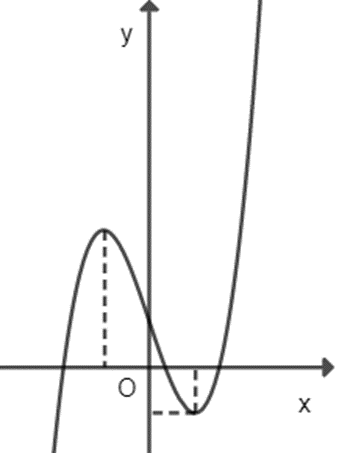
A. a > 0, b > 0, C > 0, d > 0;
B. a > 0, c > 0 > b, d < 0;
C. a > 0, b > 0, c > 0, d > 0;
D. a > 0, b < 0, c < 0, d > 0.
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vec dưới. Hỏi phương trình [f(x)]2 = 4 có bao nhiêu nghiệm?
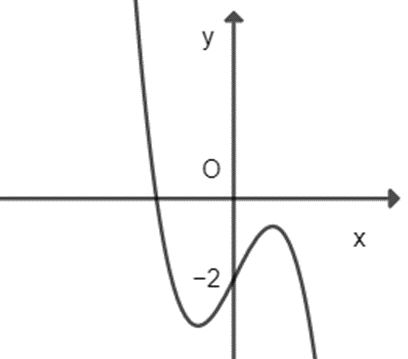
A. 6;
B. 4;
C. 5;
D. 3.
Cho hàm số y = x3 + 3x2 + m có đồ thị (C). Biết đồ thị (C) cắt trục hoành tạị 3 điểm phân biệt A, B, C sao cho B là trung điểm của AC. Phát biểu nào sau đây đúng?
A. m ∈ (0; +∞);
B. m ∈ (−∞; −4);
C. m ∈ (−4; 0);
D. m ∈ (−4; −2).
Cho hàm số y = x4 + 8x2 + m có giá trị nhỏ nhất trên [1; 3] bằng 6. Tham số thực m bằng
A. −42;
B. 6;
C. 15;
D. −3.
Cho hàm số y = x4 – 2mx2 + m. Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị:
A. m > 0;
B. m ≥ 0;
C. m < 0;
D. m ≤ 0.
Cho hình nón (N) có đỉnh S, bán kinh đáy bằng \(\sqrt 3 a\) và độ dài đường sinh bằng 4a. Gọi (T) là mặt cầu đi qua S và đường tròn đáy của (N). Bán kính của (T) bằng:
A. \(\frac{{2\sqrt {10} a}}{3}\);
B. \(\frac{{16\sqrt {13} a}}{{13}}\);
C. \(\frac{{8\sqrt {13} a}}{{13}}\);
D. \(\sqrt {13} a\).
Cho hình nó (N) có đỉnh S, bán kính đáy bằng a và độ dài đường sinh bằng 4a. Gọi (T) là mặt cầu đi qua S và đường tròn đáy của (N). Bán kính của (T) bằng:
A. \(\frac{{2\sqrt 6 a}}{3}\);
B. \(\frac{{16\sqrt {15} a}}{{15}}\);
C. \(\frac{{8\sqrt {15} a}}{{15}}\);
D. \(\sqrt {15} a\).
Cho tam giác đều ABC nội tiếp đường tròn tâm I đường kính AA’, M là trung điểm của BC. Khi quay tam giác ABM cùng với nửa hình tròn đường kính AA’ xung quanh đường thẳng AM (như hình vẽ minh họa), ta được khối nón và khối cầu có thể tích lần lượt là V1 và V2. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
A. \(\frac{9}{4}\);
B. \(\frac{{27}}{{32}}\);
C. \(\frac{4}{9}\);
D. \(\frac{9}{{32}}\).
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(\sqrt[3]{{m + 3\sqrt[3]{{m + 3\sin x}}}} = \sin x\) có nghiệm thực?
A. 5;
B. 7;
C. 3;
D. 2.
Có bao nhiêu giá trị nguyên của m để phương trình \(\sqrt 3 \sin x - \cos x = 2m\) có nghiệm trên đoạn \(\left[ {\frac{\pi }{6};\frac{{7\pi }}{6}} \right]\)?
A. 2;
B. 3;
C. 4;
D. 5.
Một lớp có 45 học sinh trong đó có 20 nam. Có bao nhiêu cách chọn ra một ban cán sự gồm 4 học sinh nếu có ít nhất 1 học sinh nam?
A. 136345;
B. 234556;
C. 236477;
D. 564543.
Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4 cm được thiết diện là một hình tròn có diện tích 9p cm2. Tính thể tích khối cầu (S).
A. \(\frac{{250\pi }}{3}\) cm3;
B. \(\frac{{2500\pi }}{3}\) cm3;
C. \(\frac{{25\pi }}{3}\) cm3;
D. \(\frac{{500\pi }}{3}\) cm3.
Hai bạn Bình và Lan cùng dự thi trong kì thi THPT Quốc gia 2018 và ở hai phòng thi khác nhau. Mỗi phòng thi có 24 thí sinh, mỗi môn thi có 24 mã đề khác nhau. Đề thi được sắp xếp và phát cho thí sinh một cách ngẫu nhiên. Xác suất để hai môn thi Toán và Tiếng Anh, Bình và Lan có chung một mã đề thi bằng nhau là
A. \(\frac{{32}}{{135}}\).
B. \(\frac{{46}}{{2209}}\);
C. \(\frac{{23}}{{288}}\);
D. \(\frac{{23}}{{576}}\).
Rút gọn biểu thức \(Q = {b^{\frac{5}{3}}}:\sqrt[3]{b}\) với b > 0
A. Q = b2;
B. \(Q = {b^{\frac{5}{9}}}\);
C. \(Q = {b^{ - \frac{4}{3}}}\);
D. \(Q = {b^{\frac{4}{3}}}\).
Số các giá trị nguyên của tham số m để hàm số y = x3 – mx2 + (m2 – 2m)x có cực tiểu tại x = 0 là
A. cô số;
B. 3;
C. 2;
D. 4.
Số nghiệm thực của phương trình \[{2^{2x + 1}}\left( {1 - {2^{3{x^2}}}} \right) = {3^{4x + 2}}\left( {{3^{6{x^2}}} - 1} \right)\] là
A. 1;
B. 2;
C. 3;
D. 4.
Tổng lập phương các nghiệm thực của phương trình \({3^{{x^2} - 4x + 5}} = 9\) là
A. 26;
B. 27;
C. 28;
D. 29.
Trên một tấm bìa catton có ghi 4 mệnh đề sau:
(I) Trên tấm bìa này có đúng một mệnh đề sai.
(II) Trên tấm bìa này có đúng hai mệnh đề sai.
(III) Trên tấm bìa này có đúng ba mệnh đề sai.
(IV) Trên tấm bìa này có đúng bốn mệnh đề sai.
Hỏi trên tấm bìa trên có bao nhiêu mệnh đề sai?
A. 4;
B. 1;
C. 2;
D. 3;
Tính diện tích hình phẳng giới hạn bởi y = x2; \(y = \frac{{{x^2}}}{{27}}\); \(y = \frac{{27}}{x}\).
A. \(\frac{{728}}{3} - 27\ln 3\);
B. 27ln3;
C. \(27\ln 3 - \frac{{52}}{3}\);
D. \(\frac{{676}}{3} - 27\ln 3\).
Tập nghiệm của bất phương trình \({\left( {\frac{2}{3}} \right)^x} > 0\) là
A. (−∞; 0);
B. (1; + ∞);
C. (0; 1);
D. ℝ.
Xác định m để đồ thị của hàm số y = 2x + 3 song song với đồ thị hàm số
y = (m2 – 2m + 2)x + 2m – 1.
A. m = 1;
B. m = 2;
C. m = 0;
D. m = −1.
Tìm m để \(\left| {4x - 2m - \frac{1}{2}} \right| > - {x^2} + 2x + \frac{1}{2} - m\) với mọi x.
A. m > 3;
B. m < 1,5;
C. m > 1,5;
D. −2 < m < 3.
Tính đạo hàm của hàm số y = 5x:
A. y′ = x.5x–1;
B. y′ = 5x;
C. \[y' = \frac{{{5^x}}}{{\ln 5}}\];
D. y′ = 5x.ln5.
Cho 2 số thực x, y thỏa mãn \({\log _2}\frac{{{x^2} + {y^2}}}{{3xy + {x^2}}} + {x^2} + 2{y^2} + 1 \le 3xy\). Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{{2{x^2} - xy + 2{y^2}}}{{2xy - {y^2}}}\).
A. \(\frac{3}{2}\);
B. \(\frac{5}{2}\);
C. \(\frac{1}{2}\);
D. \(\frac{7}{2}\).
Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi M là trung điểm của AB. Mp(P) qua M và song song với BC và CD cắt tứ diện theo 1 thiết diện là
A. Một tam giác cân;
B. Một tam giác đều;
C. Một hình bình hành;
D. Một tứ giác.
Có 5 bạn học sinh trong đó có hai bạn là Lan và Hồng. Có bao nhiêu cách xếp 5 học sinh trên thành một hàng dọc sao cho hai bạn Lan và Hồng đứng cạnh nhau?
A. 48;
B. 24;
C. 6;
D. 120.
Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc?
A. 1;
B. 25;
C. 5;
D. 120.
Một khối trụ bán kính đáy là \(a\sqrt 3 \), chiều cao là \(2a\sqrt 3 \). Tính thể tích khối cầu ngoại tiếp khối trụ.
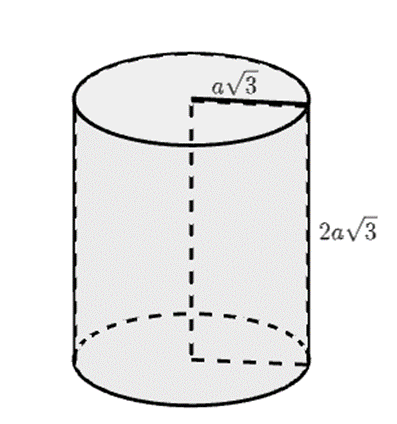
A. \(8\sqrt 6 \pi {a^3}\);
B. \(6\sqrt 6 \pi {a^3}\);
C. \(4\sqrt 3 \pi {a^3}\);
D. \(\frac{{4\sqrt 6 }}{3}\pi h{a^3}\).
Cho hình tứ diện S.ABC có SA, SB, SC đôi một vuông góc. SA = 3a, SB = 2a, SC = a. Tính thể tích khối tứ diện S.ABC.
A. \[\frac{{{a^3}}}{2}\];
B. 2a3;
C. a3;
D. 6a3.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\) là:
A. \(\frac{1}{4}\);
B. \(\frac{5}{8}\);
C. \(\frac{3}{8}\);
D. \(\frac{1}{2}\).
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn \(\overrightarrow {MA} \left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) là
A. một điểm;
B. một tia;
C. một đường thẳng;
D. một đường tròn.
Nghiệm của phương trình 2x + 2x+1 = 3x + 3x+1 là
A. x = 1;
B. \(x = {\log _{\frac{4}{3}}}\frac{2}{3}\);
C. x = 0;
D. \(x = {\log _{\frac{3}{2}}}\frac{3}{4}\).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm 0, cạnh AB = a, \(BC = a\sqrt 3 \), tam giác SAC vuông tại S. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm H của đoạn AO. Thể tích khối chóp SABC là
A. \(\frac{{{a^3}}}{2}\);
B. \(\frac{{{a^3}}}{4}\);
C. \(\frac{{{a^3}}}{6}\);
D. \(\frac{{{a^3}}}{8}\).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để phương trình f[f(x) + m] = 0 có đúng 3 nghiệm phân biệt.
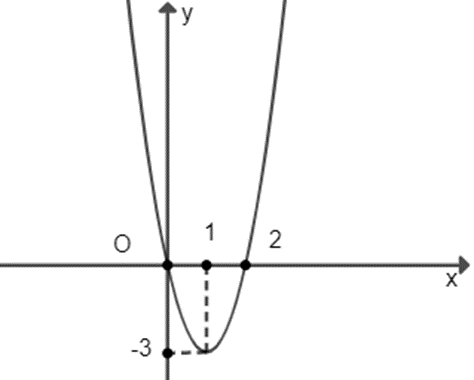
A. 1;
B. 2;
C. 3;
D. 4.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \(a\sqrt 2 \). Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \(\frac{4}{3}{a^3}\). Tính khoảng cách từ B đến mặt phẳng (SCD).
A. \(h = \frac{2}{3}a\);
B. \(h = \frac{4}{3}a\);
C. \(h = \frac{8}{3}a\);
D. \(h = \frac{3}{4}a\).
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt phẳng (ABC) một góc 60°. Thể tích khối lăng trụ ABC.A'B'C' bằng
A. \(\frac{{{a^3}\sqrt 3 }}{2}\);
B. \(\frac{{3{a^3}\sqrt 3 }}{4}\);
C. \(\frac{{{a^3}\sqrt 3 }}{8}\);
D. \(\frac{{3{a^3}\sqrt 3 }}{8}\).
Cho lăng trụ ABCD.A’B’C’D’ có ABCD là hình chữ nhật có AA’ = A’B = A’D. Tính thể tích của khối lăng trụ ABCD.A’B’C’D’ biết AB = a, \(AD = a\sqrt 3 \), AA’ = 2a.
A. \(3{a^3}\sqrt 3 \);
B. \({a^3}\sqrt 3 \);
C. a3;
D. 3a3.

