26 CÂU HỎI
Tìm tất cả các giá trị thực của tham số m để hàm số y = x3 – 3mx2 – 9m2x nghịch biến trên khoảng (0; 1).
A. m và m ≤ -1.
B.
C. m < -1.
D.
Điền từ thích hợp vào chỗ trống: Hai điểm M, N gọi là đối xứng nhau qua điểm I nếu .....
A. I là trung điểm của đoạn MN.
B. I là điểm nằm ngoài đoạn MN.
C. I là điểm cách M một khoảng bằng
D. I là điểm chia đoạn MN thành tỉ số 2 : 3.
Cho hai tam giác ABC và A'B'C' lần lượt có trọng tâm là G và G' Đẳng thức nào sau đây là sai?
A.
B.
C.
D.
Gieo một đồng xu và một con xúc sắc. Số phần tử của không gian mẫu là:
A. 24.
B. 12.
C. 6.
D. 8.
Cho hình chữ nhật ABCD có AB = a và Gọi K là trung điểm của cạnh AD. Tính
A.
B.
C.
D.
Tìm số quy tròn của phép tính sau: 374 529 ± 200.
A. 374 000.
B. 375 000.
C. 376 000.
D. 377 000.
Xét các số phức z và w thỏa mãn |z – 2w| = 4 và |3z + w| = 5. Khi |5z – 3w + i| đạt giá trị nhỏ nhất, |z – w + 1| bằng
A.
B. 4
C. 2
D.
Cho số phức z thỏa mãn |z – 3 – 4i| = 1. Môđun lớn nhất của số phức z là
A. 7.
B. 6.
C. 5.
D. 4.
Cho lục giác đều ABCDEF tâm O như hình vẽ dưới đây. Phép tịnh tiến theo véctơ biến hình thoi ABOF thành hình thoi nào sau đây?
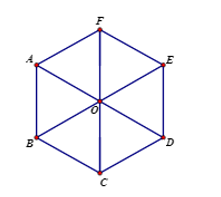
A. OBCD.
B. OAFE
C. ODEF.
D. OCDE.
Cho lục giác đều ABCDEF, tâm O, các đỉnh được đặt theo thứ tự đó và cùng chiều kim đồng hồ. Thực hiện lần lượt phép quay tâm O góc quay và phép tịnh tiến theo vectơ thì ảnh của tam giác ABO là:
A. ∆BOC.
B. ∆OCD.
C. ∆OFE.
D. ∆AOF.
Hàm số nào trong các hàm số sau có đồ thị nhận trục Oy làm trục đối xứng?
A.
B.
C. y = tan x.
D.
Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là:
A. 19.
B. 18.
C. 31.
D. 49.
Cho hình bình hành ABCD, đường cao ứng với cạnh DC là AH = 6 cm, cạnh DC = 12 cm. Diện tích của hình bình hành ABCD là
A. 72 cm2.
B. 82 cm2.
C. 92 cm2.
D. 102 cm2.
Kết luận nào đúng về số thực a nếu .
A. a < 1.
B. a > 0.
C. 0 < a < 1.
D. a < 0.
Cho tam giác (ABC). Để điểm M thỏa mãn điều kiện thì M phải thỏa mãn mệnh đề nào?
A. M là điểm sao cho tứ giác ABMC là hình bình hành.
B. M là trọng tâm tam giác ABC.
C. M là điểm sao cho tứ giác BAMC là hình bình hành.
D. M thuộc trung trực của AB.
Cho hai đường thẳng d và d’ song song có bao nhiêu phép tịnh tiến biến đường thẳng d thành đường thẳng d’:
A. Không có phép tịnh tiến nào.
B. Có duy nhất một phép tịnh tiến.
C. Có 2 phép tịnh tiến.
D. Có vô số phép tịnh tiến.
Trong mặt phẳng tọa độ Oxy cho hai điểm M(-10; 1) và M’(3; 8). Phép tịnh tiến theo véctơ biến điểm M thành M’. Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Cho a là số thực dương tùy ý khác 1. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Trong không gian Oxyz, cho hai điểm A(3; 5; -1) và B(1; 1; 3). Tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho nhỏ nhất là
A. M(2; 3; 0).
B. M(2; -3; 0).
C. M(-2; 3; 0).
D. M(-2; -3; 0).
Nghiệm của phương trình cos x = 1 là
A.
B.
C.
D.
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = xex, y = 0, x = 0, x = 1 xung quanh trục Ox là
A.
B.
C.
D.
Trong mặt phẳng tọa độ Oxy cho đường tròn và đường tròn d: x – y + 2 = 0, phương trình đường tròn là ảnh của đường tròn qua phép đối xứng trục d là
A.
B.
C.
D.
Tìm các giá trị của m để hàm số y = x2 + mx + 5 luôn đồng biến trên (1; +∞).
A. m < -2.
B. m ≥ -2.
C. m = -4.
D. Không xác định được.
Tìm tất cả các giá trị thực của tham số m để hàm số y = -x2 + (m – 1)x + 2 nghịch biến trên khoảng (1; 2).
A. m < 5.
B. m > 5.
C. m ≤ 3.
D. m > 3.
Cho hai tập hợp X = {x ∈ ℕ| x là bội số chung của 4 và 6}, Y = {x ∈ ℕ| x là bội số của 12}. Trong các mệnh đề sau, mệnh đề nào sai?
A.
B.
C.
D. và
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
