48 CÂU HỎI
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?
A. (0; 0)
B. (40; 0)
C. (20; 40)
D. (50; 0)
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm (I) và (II). Mỗi sản phẩm (I) bán lãi 500 nghìn đồng, mỗi sản phẩm (II ) bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm (I) thì Chiến phải làm việc trong (3) giờ, Bình phải làm việc trong (1) giờ. Để sản xuất được một sản phẩm (II) thì Chiến phải làm việc trong (2) giờ, Bình phải làm việc trong (6) giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá (180) giờ và Bình không thể làm việc quá (220) giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là:
A. 32 triệu đồng
B. 35 triệu đồng
C. 14 triệu đồng
D. 30 triệu đồng
Cho tam giác ABC có a2 + b2 ‒ c2 > 0. Khi đó:
A. \[\widehat C > 90^\circ .\]
B. \[\widehat C < 90^\circ .\]
C. \[\widehat C = 90^\circ .\]
D. Không thể kết luận được gì về góc C.
Cho đường tròn (C):x2 + y2 ‒ 2x + 2y ‒ 7 = 0 và đường thẳng d: x + y + 1 = 0. Tìm tất cả các đường thẳng song song với đường thẳng d và cắt đường tròn (C) theo dây cung có độ dài bằng 2.
A. x+y+4=0và x+y−4=0.
B.x+y+2=0.
C.x+y+4=0.
D.x+y+2=0và x+y−2=0.
Cho hai điểm A(1; ‒2; 0), B(0; 1; 1), độ dài đường cao OH của tam giác OAB là:
A. \(3\sqrt {19} \)
B. \(\frac{{3\sqrt {19} }}{{13}}\)
C. \(\sqrt 6 \)
D. \(\frac{{\sqrt {66} }}{{11}}\)
Có bao nhiêu giá trị nguyên của m để phương trình \[\sqrt 3 \sin x - \cos x = m\] có nghiệm trên đoạn \[\left[ {\frac{\pi }{6};\frac{{7\pi }}{6}} \right]\]
A. 2
B. 3
C. 4
D. 5
Có hai chiếc hộp chứa viên bi. Hộp thứ nhất chứa 4 viên bi đỏ, 3 viên bi trắng. Hộp thứ hai chứa 2 viên bi đỏ, 4 viên bi trắng. Lấy ngẫu nhiên từ mỗi hộp ra 1 viên bi, tính xác suất để 2 viên bi được lấy ra có cùng màu.
A. \[\frac{{10}}{{21}}\]
B. \[\frac{{10}}{{39}}\]
D. \[\frac{{11}}{{39}}\]
D. \[\frac{{11}}{{39}}\]
Rút gọn biểu thức \[P = {x^{\frac{1}{3}}} \cdot \sqrt[6]{x},\] x > 0
A. P = x2.
B. \[P = \sqrt x .\]
C. \[P = {x^{\frac{1}{8}}}.\]
D. \[P = {x^{\frac{2}{9}}}.\]
Cho hình chữ nhật ABCD có AB = a và \(AD = a\sqrt 2 \). Gọi K là trung điểm của cạnh AD. Tính \(\overrightarrow {BK} \cdot \overrightarrow {AC} .\)
A. \(\overrightarrow {BK} \cdot \overrightarrow {AC} = 0.\)
B. \(\overrightarrow {BK} \cdot \overrightarrow {AC} = - {a^2}\sqrt 2 .\)
C. \(\overrightarrow {BK} \cdot \overrightarrow {AC} = {a^2}\sqrt 2 .\)
D. \(\overrightarrow {BK} \cdot \overrightarrow {AC} = 2{a^2}.\)
Trên giá sách có 10 quyển Văn khác nhau, 8 quyển sách Toán khác nhau và 6 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?
A. 230400
B. 60
C. 48
D. 188
Thầy X có 15 cuốn sách gồm 4 cuốn sách toán, 5 cuốn sách lí và 6 cuốn sách hóa. Các cuốn sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn.
A. \[\frac{5}{6}.\]
B. \[\frac{{611}}{{715}}.\]
C. \[\frac{{600}}{{713}}.\]
D. \[\frac{6}{7}.\]
Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính r bằng
A. πrl.
B. 2πrl.
C. \[\frac{1}{3}\pi rl.\]
D. 4πrl.
Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
A. A(1; 5).
B. A(‒3; ‒1).
C. A (‒2; ‒7).
D. A(1; ‒10).
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(1; 2), M'(−2; −4) và số k = 2. Phép vị tự tỉ số k = 2 biến điểm M thành điểm M’ có tâm vị tự là:
A. I(‒4; 8).
B. I(4; ‒8).
C. I(‒4; ‒8).
D. I(4; 8).
Trong hệ trục \[\left( {O;\overrightarrow i ;\overrightarrow j } \right)\] tọa độ của vectơ \[\overrightarrow i + \overrightarrow j \]là:
A. (‒1; 1).
B. (1; 0).
C. (0; 1).
D. (1; 1).
Cho phương trình bậc hai Az2 ‒ Bz + C . Biệt thức của phương trình được tính bởi:
A. B2 ‒ 4AC.
B. A2 ‒ 4BC.
C. C2 ‒ 4BA.
D. B2 ‒ AC.
tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 3MC. Khi đó, biễu diễn \(\overrightarrow {AM} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là:
A. \(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + 3\overrightarrow {AC} .\)
B. \(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} .\)
C. \(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} .\)
D. \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} .\)
Cho hai đa thức f(x) và g(x). Xét các tập hợp:
\(A = \left\{ {x \in R\mid f\left( x \right) = 0} \right\}\)
\(B = \left\{ {x \in R\mid g\left( x \right) = 0} \right\}\)
\(C = \left\{ {x \in R\mid \frac{{f\left( x \right)}}{{g\left( x \right)}} = 0} \right\}\)
Trong các mệnh đề sau, mệnh đề nào đúng?
A. C = A ∪ B.
B. C = A.
C. C = A ∖ B.
D. C = B ∖ A.
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \(\frac{{{a^3}}}{6}\). Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
A. \(r = \frac{a}{{3 + \sqrt 3 }}.\)
B. r = 2a.
C. \(r = \frac{a}{{3\left( {3 + 2\sqrt 3 } \right)}}.\)
D. \(r = \frac{{2a}}{{3\left( {3 + 2\sqrt 3 } \right)}}.\)
Cho tứ diện đều ABCD có một đường cao AA1. Gọi I là trung điểm AA1. Mặt phẳng (BCI) chia tứ diện ABCD thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó.
A. \(\sqrt {\frac{{43}}{{51}}} .\)
B. \(\frac{1}{2}.\)
C. \(\frac{1}{4}.\)
D. \(\sqrt {\frac{{48}}{{153}}} .\)
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyếncủa (SAB) và (SCD) là
A. Đường thẳng qua S và song song với AD.
B. Đường thẳng qua S và song song với CD.
C. Đường SO với O là tâm hình bình hành.
D. Đường thẳng qua S và cắt AB.
Tổng số cạnh và số đỉnh của hình bát diện đều bằng bao nhiêu ?
A. 18
B. 14
C. 12
D. 20
Tính đạo hàm của hàm số \(y = {2^{{x^2}}}.\)
A. \(y' = \frac{{x \cdot {2^{1 + {x^2}}}}}{{{\rm{ln}}2}}.\)
B. \(y' = x \cdot {2^{1 + {x^2}}} \cdot {\rm{ln}}2.\)
C. \(y' = {2^x} \cdot {\rm{ln}}{2^x}.\)
D. \(y' = \frac{{x \cdot {2^{1 + x}}}}{{{\rm{ln}}2}}.\)
Trong hệ tọa độ Oxy cho ba điểm A(0; ‒3),B(2;1),D(5;5). Tìm tọa độ điểm C để tứ giác ABCD là hình bình hành.
A. C (3; 1).
B. C (‒3; ‒1).
C. C(7; 9).
D. C(‒7; ‒9).
Trong mặt phẳng tọa độ \(Oxy\) cho bốn điểm A(3; ‒2); B(7; 1); C(0; 1); D(‒8; ‒5). Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} ,\overrightarrow {CD} \) đối nhau
B. \(\overrightarrow {AB} ,\overrightarrow {CD} \) cùng phương nhưng ngược hướng.
C. \(\overrightarrow {AB} ,\overrightarrow {CD} \) cùng phương cùng hướng.
D. \(A,B,C,D\) thẳng hàng.
Cho hình hộp ABCD.A'B'CD' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60°. Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A. \(\frac{{\sqrt {22} }}{{11}}\).
B. \(\frac{2}{{11}}\).
C. \(\frac{{\sqrt 2 }}{{11}}\).
D. \(\frac{3}{{11}}\).
Đồ thị hàm số y = (3 ‒ m)x + m + 3 đi qua gốc tọa độ khi:
A. m = ‒3.
B. m = 3.
C. m ≠ 3.
D. m ≠ ± 3.
Đường thẳng d đi qua gốc tọa độ O và song song với đường thẳng – x + 2y + 3 = 0 có phương trình tham số là:
A. \(d:\left\{ {\begin{array}{*{20}{l}}{x = - 1}\\{y = 2}\end{array}} \right.\);
B. \(d:\left\{ {\begin{array}{*{20}{l}}{x = 2t}\\{y = t}\end{array}} \right.\);
C. \(d:\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = - 2t}\end{array}} \right.\);
D. \(d:\left\{ {\begin{array}{*{20}{l}}{x = - 2t}\\{y = t}\end{array}} \right.\).
Trong một môn học, Thầy giáo có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu trung bình và 15 câu dễ. Từ 30 câu hỏi đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu hỏi khác nhau, sao cho trong mỗi đề nhất thiết phải có đủ cả 3 câu (khó, dễ, trung bình) và số câu dễ không ít hơn 2 ?
A. 41811.
B. 42802.
C. 56875.
D. 32023.
Nước ta có diện tích 331212 km2, dân cư 90 triệu dân. Vậy mật độ dân số nước ta là:
A. 227 người/km2.
B. 722 người/km2.
C. 277 người/km2.
D. 272 người/km2.
Giá trị nhỏ nhất của biết thức F = y - x trên miền xác định bởi hệ \[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\] là:
A. min F = 1 khi x = 2; y = 3.
B. min F =2 khi x = 0; y = 2.
C. min F = 3 khi x = 1; y = 4.
D. min F = 0 khi x = 0; y = 0.
Trong không gian Oxyz, cho điểm A(3;0;0),B(0;−2;0)và C(0;0;−4). Mặt cầu ngoại tiếp tứ diện OABC có diện tích bằng:
A. 116π.
B. 29π.
C. 16π.
D. \[\frac{{29\pi }}{4}.\]
Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:
A.0.24.
B.0.96.
C. 0.46.
D.0.92.
Cho hai điểm A(1;2; ‒1) và B(‒1;3;1). Tọa độ điểm M nằm trên trục tung sao cho tam giác ABM vuông tại M .
A. M(0; 1; 0) hoặc M(0; 4; 0)
B. M(0; 2; 0) hoặc M(0; 3; 0)
C. M(0; ‒1; 0) hoặc M(0; ‒4; 0)
D. M(0; ‒2; 0) hoặc M(0; ‒3; 0)
Trong mặt phẳng tọa độ Oxy cho hai điểm A(2;2), B(5; ‒2). Tìm điểm M thuộc trục hoành sao cho \[\widehat {AMB} = 90^\circ \]
A. M(0; 1).
B. M(6; 0); (1; 0)
C. M(1; 6).
D. M(0; 6).
Cho ba điểm A, B, C không thẳng hàng và điểm M thỏa mãn đẳng thức vectơ \(\overrightarrow {AM} = x\overrightarrow {AB} + y\overrightarrow {AC} \). Đặt \(\overrightarrow {MA} = x\overrightarrow {MB} + y\overrightarrow {MC} \). Tính giá trị biểu thức P = x + y.
A. P = 0.
B. P = 2.
C. P = ‒2.
D. P = 3.
Cho lục giác đều ABCDEF tâm O . Hỏi có bao nhiêu vecto khác vecto không; cùng phương với \[\overrightarrow {OC} \] có điểm đầu và điểm cuối là các đỉnh của lục giác?
A. 6.
B. 5.
C. 9.
D. 8
Có 3 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ ( các bông hoa xem như đôi 1 khác nhau) người ta muốn chọn ra một bó hoa gồm 7 bông. Có bao nhiêu cách chọn các bông hoa được chọn tuỳ ý.
A. 120
B. 136
C. 268
D. 170
Cho hàm số \(f\left( x \right) = {2^{{x^2} + 1}}\). Tính \(T = {2^{ - {x^2} - 1}} \cdot f'\left( x \right) - 2x{\rm{ln}}2 + 2\).
A. T = ‒2.
B. T = 2.
C. T = 3.
D. T = 1.
Giao điểm của parabol (P): y = x2 + 5x + 4 với trục hoành:
A. (‒1; 0); (‒4; 0).
B. (0; ‒1); (0; ‒4).
C. (‒1; 0); (0; ‒4).
D. (0; ‒1); (‒4; 0).
Cho hàm số \(f\left( x \right) = \frac{{{4^x}}}{{{4^x} + 2}}\). Tính tổng
\(S = f\left( {\frac{1}{{2019}}} \right) + f\left( {\frac{2}{{2019}}} \right) + \ldots + f\left( {\frac{{2018}}{{2019}}} \right) + f\left( 1 \right){\rm{.\;}}\)
A. \(S = \frac{{3032}}{3}.\)
B. \(S = \frac{{3023}}{3}.\)
C. \(S = \frac{{3026}}{3}.\)
D. \(S = \frac{{3029}}{3}.\)
Cho hàm số \(f\left( x \right) = \frac{{{4^x}}}{{{4^x} + 2}}\).
Tính giá trị biểu thức \({\rm{A}} = f\left( {\frac{1}{{100}}} \right) + f\left( {\frac{2}{{100}}} \right) + \ldots + f\left( {\frac{{100}}{{100}}} \right)\) ?
A. 50.
B. 49.
C. \(\frac{{149}}{3}.\)
D. \(\frac{{301}}{6}.\)
Cho 4 điểm A(1; ‒2),B(0;3),C(‒3;4),D(‒1;8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
A. A, B, C.
B. B, C, D.
C. A, B, D.
D. A, C, D.
Trong hệ trục tọa độ Oxy, cho véc-tơ \[\overrightarrow a = \left( {1; - 2} \right).\] Với giá trị nào của y thì véc-tơ \[\overrightarrow b = \left( { - 3;y} \right)\] vuông góc với \[\overrightarrow a \] ?
А. ‒3.
В. 6.
С. 3.
D. ‒6.
Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
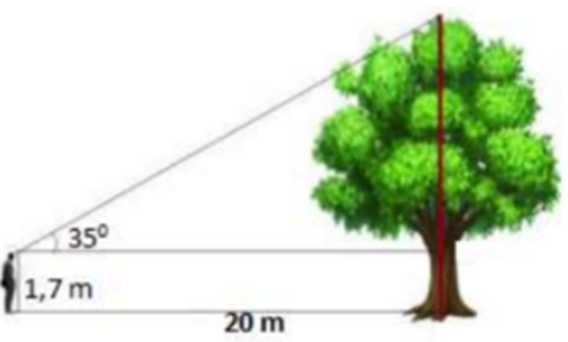
A. 14,3 m.
B. 15,7 m.
C. 16,8 m.
D. 17,2 m.
Tìm m để phương trình x2 − (2m + 1)x + m2 + 1=0 có 2 nghiệm x1; x2 thỏa mãn x2 = 2x1.
A. m = 1, m = 7.
B. m = 2, m = 7.
C. m = 1, m = 5.
D. m = 1, m = 0.
Trong mặt phẳng với hệ trục tọa độ Oxy, cho các vectơ sau: \[\overrightarrow a = 4\overrightarrow i - 3\overrightarrow j ,\overrightarrow b = 2\overrightarrow j .\] Trong các khẳng định sau khẳng định nào sai:
A. \[\overrightarrow b = \left( {0;2} \right).\]
B. \[\overrightarrow a = \left( {4; - 3} \right).\]
C. \[\left| {\overrightarrow a } \right| = \left( {4; - 3} \right).\]
D. \[\left| {\overrightarrow b } \right| = \sqrt 2 .\]
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (không kể bờ là đường thẳng)?
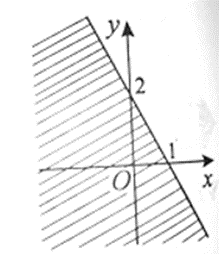
A. 2x + y ‒ 2 < 0.
B. 2x + y + 2 > 0.
C. 2x + y + 2 < 0.
D. 2x + y ‒ 2 > 0.

