33 CÂU HỎI
Cho tam giác đều ABC. Mệnh đề nào sau đây là sai?
A. \(\overrightarrow {AB} = \overrightarrow {BC} \)
B. \(\overrightarrow {AB} \ne \overrightarrow {BC} \)
C. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)
D. \(\overrightarrow {AC} \) không cùng phương \(\overrightarrow {BC} \).
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Gọi P là xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ. Khi đó P bằng:
A. \(\frac{{100}}{{231}}\)
B. \(\frac{{115}}{{231}}\)
C. \(\frac{1}{2}\)
D. \(\frac{{118}}{{231}}\).
Đạo hàm của hàm số y = x + ln2x là:
A. \(y' = 1 + \frac{{2\ln {\rm{x}}}}{x}\)
B. y’ = 1 + 2lnx
C. \(y' = 1 + \frac{2}{{x\ln {\rm{x}}}}\)
D. y’ = 1 + 2xlnx.
Hàm số \(y = {\left( {{x^2} - 16} \right)^{ - 5}} - \ln \left( {24 - 5{\rm{x}} - {x^2}} \right)\) có tập xác định là:
A. (–8; –4) ∪ (3; +∞)
B. (–∞;–4) ∪ (3; +∞)
C. (–8; 3) \ {–4}
D. (–4; 3).
Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a.
A. \(V = \frac{{3\pi {a^3}}}{4}\)
B. \(V = \pi {a^3}\)
C. \(V = \frac{{\pi {a^3}}}{6}\)
D. \(V = \frac{{\pi {a^3}}}{2}\).
Cho số phức \[{\rm{z}} = 1 + \sqrt 3 i\]. Khi đó:
A. \(\frac{1}{z} = \frac{1}{2} - \frac{{\sqrt 3 }}{2}i\)
B. \(\frac{1}{z} = \frac{1}{2} + \frac{{\sqrt 3 }}{2}i\)
C. \(\frac{1}{z} = \frac{1}{4} + \frac{{\sqrt 3 }}{4}i\)
D. \(\frac{1}{z} = \frac{1}{4} - \frac{{\sqrt 3 }}{4}i\).
Trong không gian với hệ tọa Oxyz, cho vectơ \(\overrightarrow a = \left( {1; - 2;4} \right),\overrightarrow b = \left( {{x_0};{y_0};{z_0}} \right)\) cùng phương với vectơ \(\overrightarrow a \). Biết vectơ \(\overrightarrow b \) tạo với tia Oy một góc nhón và \(\left| {\overrightarrow b } \right| = \sqrt {21} \). Giá trị của tổng x0 + y0 + z0 bằng:
A. –3
B. 6
C. –6
D. 3.
Trong mặt phẳng Oxy cho \(\overrightarrow a \left( {1;3} \right)\) và \(\overrightarrow b \left( { - 2;1} \right)\). Tích vô hướng \(\overrightarrow a .\overrightarrow b \) là:
A. –1
B. 2
C. 1
D. 4.
Đỉnh của parabol y = x2 + x + m nằm trên đường thẳng \(y = \frac{3}{4}\) nếu m bằng:
A. Một số tùy ý
B. 3
C. 5
D. 1.
Tìm tập nghiệm S của bất phương trình \({\log _{2 - \sqrt 3 }}\left( {2{\rm{x}} - 1} \right) < {\log _{2 - \sqrt 3 }}\left( {3{\rm{x}} - 2} \right)\).
A. \(\left( {\frac{1}{2};\frac{2}{3}} \right)\)
B. \(\left( {\frac{1}{2};1} \right)\)
C. \(\left( {\frac{2}{3};1} \right)\)
D. (1; +∞).
Có ba chiếc hộp, mỗi chiếc hộp chứa ba chiếc thẻ được đánh số 1, 2, 3. Từ mỗi hộp rút ngẫu nhiên một chiếc thẻ. Xác suất để ba cái thẻ được rút ra có tổng bẳng 6 là?
A. \(\frac{2}{9}\)
B. \(\frac{1}{{27}}\)
C. \(\frac{7}{{27}}\)
D. \(\frac{8}{{27}}\).
Tìm nghiệm dương nhỏ nhất x0 của \(3\sin 3{\rm{x}} - \sqrt 3 cos9{\rm{x}} = 1 + 4{\sin ^3}3{\rm{x}}\).
A. \[{{\rm{x}}_0} = \frac{\pi }{2}\]
B. \[{{\rm{x}}_0} = \frac{\pi }{{18}}\]
C. \[{{\rm{x}}_0} = \frac{\pi }{{24}}\]
D. \[{{\rm{x}}_0} = \frac{\pi }{{54}}\].
Biết phương trình \({9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2{\rm{x}} - 1}}\) có nghiệm là a.
Tính giá trị biểu thức \[P = a + \frac{1}{2}{\log _{\frac{9}{2}}}2\].
A. \(P = \frac{1}{2}\)
B. P = 1
C. \[P = 1 - \frac{1}{2}{\log _{\frac{9}{2}}}2\]
D. \[P = 1 - {\log _{\frac{9}{2}}}2\].
Trong mặt phẳng tọa độ Oxy. Cho hai đường thẳng ∆1 và ∆2 lần lượt có phương trình x – 2y + 1 = 0 và x – 2y + 4 = 0, điểm I(2; 1). Phép vị tự tâm I tỉ số k biến đường thằng ∆1 thành ∆2 khi đó giá trị của k là:
A. 1
B. 2
C. 3
D. 4.
Trong mặt phẳng Oxy cho điểm M(1; 1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay 45°.
A. \(\left( {0;\sqrt 2 } \right)\)
B. (–1; 1)
C. (1; 0)
D. \(\left( { - \sqrt 2 ;0} \right)\).
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y + 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép quay tâm O góc quay –90°.
A. d’: x + 3y + 2 = 0.
B. d’: x + 3y – 2 = 0.
C. d’: 3x – y – 6 = 0.
D. d’: x – 3y – 2 = 0.
Số nghiệm của phương trình \(cos\left( {\frac{x}{2} + \frac{\pi }{4}} \right) = 0\) trong khoảng (π; 8π) là:
A. 2
B. 4
C. 3
D. 1.
Điểm M0(1; 0) thuộc miền nghiệm của hệ bất phương trình:
A. \(\left\{ \begin{array}{l}2{\rm{x}} - y > 3\\10{\rm{x}} + 5y \le 8\end{array} \right.\)
B. \(\left\{ \begin{array}{l}2{\rm{x}} - y > 3\\10{\rm{x}} + 5y \ge 8\end{array} \right.\)
C. \(\left\{ \begin{array}{l}2{\rm{x}} - y \le 3\\10{\rm{x}} + 5y > 8\end{array} \right.\)
D. \(\left\{ \begin{array}{l}2{\rm{x}} - y \le 3\\10{\rm{x}} + 5y < 8\end{array} \right.\).
Cho hai tập hợp A = (m – 1; 5) và B = (3; +∞). Tìm tất cả các giá trị thực của tham số m để A\B = ∅.
A. m ≥ 4
B. m = 4
C. 4 ≤ m < 6
D. 4 ≤ m ≤ 6.
Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc với OA. Biết độ dài đường tròn (O) là 4π (cm). Độ dài cung lớn BC là:
A. \(\frac{{4\pi }}{3}\)
B. \(\frac{{5\pi }}{3}\)
C. \(\frac{{7\pi }}{3}\)
D. \(\frac{{8\pi }}{3}\).
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?
A. (0; 0)
B. (40; 0)
C. (20; 40)
D. (50; 0).
Cho phương trinhg: x2 + 2(m – 1)x – (m + 1) = 0. Tìm m để phương trình có 2 nghiệm nhỏ hơn 2.
A. m < 2
B. m > –3
C. \(\frac{1}{3} < m < 2\)
D. \(m > \frac{1}{3}\).
Nếu \(2A_n^4 = 3{\rm{A}}_{n - 1}^4\) thì n bằng:
A. n = 11
B. n = 12
C. n = 13
D. n = 14.
Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn bệ A, B, C, D?
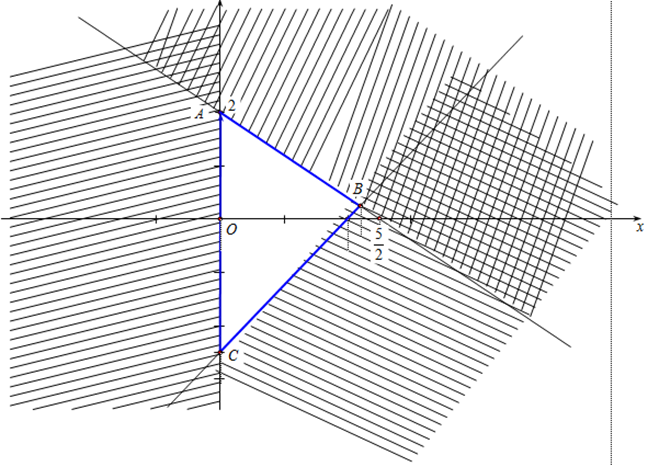
A. \(\left\{ \begin{array}{l}y \ge 0\\5{\rm{x}} - 4y \ge 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x \ge 0\\{\rm{4x}} - 5y \le 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x \ge 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x > 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\).
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng 60°, SA = 1, SB = 2, SC = 3. Thể tích của khối chóp S.ABC bằng:
A. \(\frac{{\sqrt 2 }}{{72}}\)
B. \(\frac{{\sqrt 6 }}{2}\)
C. \(\frac{{\sqrt 2 }}{2}\)
D. \(\frac{{\sqrt 3 }}{2}\).
Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?
A. Không có
B. 1
C. 2
D. Vô số.
Đường tròn nội tiếp hình vuông cạnh a có bán kính là:
A. \(a\sqrt 2 \)
B. \(\frac{{a\sqrt 2 }}{2}\)
C. \(\frac{a}{2}\)
D. \(\frac{{a\sqrt 3 }}{2}\).
Tìm số nghiệm của phương trình tanx = 1 trong khoảng (0; 7π).
A. 5
B. 7
C. 3
D. 4.
Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60°. Thể tích của khối chóp đó bằng:
A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 3 }}{6}\)
C. \(\frac{{{a^3}\sqrt 3 }}{{36}}\)
D. \(\frac{{{a^3}\sqrt 3 }}{4}\).
Tính tổng \(S = {3^{2015}}.C_{2015}^0 - {3^{2014}}.C_{2015}^2 + {3^{2013}}.C_{2015}^2 - ... + 3C_{2015}^{2014} - C_{2015}^{2015}\).
A. 22015
B. –22015
C. 32015
D. 42015.
Tìm tất cả các giá trị thực của m để phương trình x2 – 4x + 6 + 3m = 0 có nghiệm thuộc đoạn [–1; 3].
A. \(\frac{2}{3} \le m \le \frac{{11}}{3}\)
B. \(\frac{{ - 11}}{3} \le m \le \frac{{ - 2}}{3}\)
C. \( - 1 \le m \le \frac{{ - 2}}{3}\)
D. \(\frac{{ - 11}}{3} \le m \le - 1\).
Tính thể tích khối chóp tam giác đều có độ dài cạnh bên bằng \(a\sqrt 2 \) và độ dài cạnh đáy bằng a.
A. \(\frac{{{a^3}}}{{12}}\)
B. \(\frac{{{a^3}\sqrt 2 }}{6}\)
C. \(\frac{{{a^3}\sqrt 3 }}{6}\)
D. \(\frac{{{a^3}\sqrt 5 }}{{12}}\).
Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau:
− Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.
− Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B.
Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn \(\frac{1}{2}\) số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A. Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất là:
A. 500 đơn vị vitamin A và 500 đơn vị vitamin B.
B. 600 đơn vị vitamin A và 400 đơn vị vitamin B.
C. 600 đơn vị vitamin A và 300 đơn vị vitamin B.
D. 100 đơn vị vitamin A và 300 đơn vị vitamin B.

