35 CÂU HỎI
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
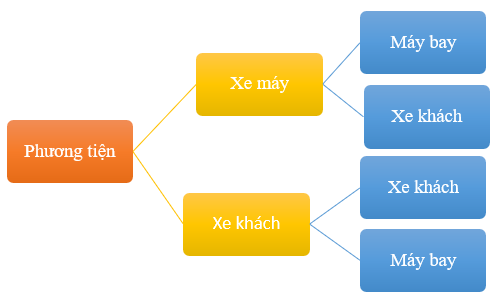
Hỏi bạn Khoa có mấy cách chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt.
A. 3;
B. 4;
C. 5;
D. 6.
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là:
A. n.k;
B. n.(n – 1).(n – 2)…(n – k + 1);
C.\(\frac{n}{k}\);
D.\(\frac{k}{n}\).
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là hai trong 8 điểm đó.
A. 28;
B. 30;
C. 56;
D. 58.
Cho biểu thức (a + b)n , với n = 4 ta có khai triển là:
A. (a + b)4 = \(C_4^0{a^4} + C_4^1{a^3}{b^1} + C_4^2{a^2}.{b^2} + C_4^3a.{b^3} + C_4^4.{b^4}\);
B. (a + b)4 = \(C_4^0{a^4} - C_4^1{a^3}{b^1} - C_4^2{a^2}.{b^2} - C_4^3a.{b^3} - C_4^4.{b^4}\);
C. (a + b)4 = \(C_4^0{a^4} - C_4^1{a^3}{b^1} + C_4^2{a^2}.{b^2} - C_4^3a.{b^3} + C_4^4.{b^4}\);
D. (a + b)4 = \( - C_4^0{a^4} - C_4^1{a^3}{b^1} - C_4^2{a^2}.{b^2} - C_4^3a.{b^3} - C_4^4.{b^4}\).
Khai triển biểu thức (a + 2b)5 ta thu được kết quả là:
A. a5 + 10a4b + 40a3b2 + 80a2b3 + 80ab4 + 32b5;
B. a5 – 10a4b – 40a3b2 – 80a2b3 – 80ab4 – 32b5;
C. a5 + 20a4b + 30a3b2 + 80a2b3 + 80ab4 + 32b5;
D. a5 + 10a4b + 40a3b2 + 60a2b3 + 60ab4 + 32b5.
Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác 0,004 nếu sai số tuyệt đối là:
A. 0,005;
B. 0,004;
C. 0,006;
D. 0,0007.
Trong một phép đo đạc, tính toán, các bạn An, Phong, Nam lần lượt có các sai số tuyệt đối sau: 0,005; 0,004; 0,003. Hỏi phép đo đạc, tính toán của bạn nào chính xác nhất ?
A. An;
B. Phong;
C. Nam;
D. Ba bạn có chất lượng phép đo đạc, tính toán như nhau.
Cho số gần đúng a = 22 648 024 với độ chính xác d = 101. Hãy viết số quy tròn của số a.
A. 22 648 000;
B. 22 649 000;
C. 22 646 000;
D. 22 647 000.
Cho bảng số liệu như sau:

Mốt của bảng số liệu là:
A. 2;
B. 3;
C. 6;
D. 4.
Kết quả kiểm tra môn Toán của các bạn Hoa, Lan, Quân, Phong, Đức lần lượt là: 9, 8, 5, 7, 10. Số trung bình cộng \(\overline x \) của mẫu số liệu trên là:
A. 7,8;
B. 7,9;
C. 7;
D. 8,8.
Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây:

Tứ phân vị Q1, Q2, Q3 của bảng số liệu này lần lượt là:
A. 8,45; 8,5; 8,7;
B. 8,5; 8,45; 8,7;
C. 8,45; 8,5; 8,6;
D. 8,5; 8,45; 8,6.
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
|
Năng suất lúa (tạ/ha) |
25 |
30 |
35 |
40 |
45 |
|
Tần số |
4 |
7 |
9 |
6 |
5 |
So sánh Q1 và Q2 ?
A. Q1 > Q2;
B. Q1 < Q2;
C. Q1 = Q2;
D. Q1 = 2Q2.
Thời gian chạy 50 m của 20 học sinh được ghi lại trong bảng dưới đây:

Khoảng biến thiên của bảng số liệu trên là:
A. 0,8;
B. 0,6;
C. 0,9;
D. 0,5.
41 học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm 30. Kết quả như sau:
|
Điểm |
9 |
11 |
14 |
16 |
17 |
18 |
20 |
21 |
23 |
25 |
|
Số lượng (tần số) |
3 |
6 |
4 |
4 |
6 |
7 |
3 |
4 |
2 |
2 |
Phương sai của bảng số liệu trên là:
A. 16,61;
B. 4,25;
C. 18,04;
D. 11,24.
Tốc độ phát triển của một loại virus trong 10 ngày với các điều kiện khác nhau (đơn vị: nghìn con) được thống kê lại như sau:
|
20 |
100 |
30 |
980 |
440 |
20 |
20 |
150 |
60 |
270 |
Khoảng tứ phân vị của mẫu số liệu trên là:
A. 230 nghìn;
B. 240 nghìn;
C. 250 nghìn;
D. 260 nghìn;
Gieo một đồng xu ba lần liên tiếp. Xác suất để xuất hiện ít nhất một lần mặt ngửa là:
A. \(\frac{7}{8}\);
B. \(\frac{1}{8}\);
C. 0,25;
D. 0,5.
Một lớp có 15 bạn nam và 17 bạn nữ. Lấy ngẫu nhiên 3 bạn để làm đội kỉ luật. Xác suất để đội kỉ luật có ít nhất một bạn nữ là:
A. \(\frac{{900}}{{992}}\);
B. \(\frac{{901}}{{992}}\);
C. \(\frac{{91}}{{992}}\);
D. \(\frac{1}{{992}}\).
Cho biến cố A có biến cố đối \(\overline A \). Khẳng định nào sau đây là đúng ?
A. 0 ≤ P(A) hoặc P(A) ≥ 1 ;
B. P(\(\overline A \)) = 1 – P(A) ;
C. 0 ≤ P(\(\overline A \)) hoặc P(\(\overline A \)) ≥ 1 ;
D. P(A) = P(\(\overline A \)).
Trong mặt phẳng tọa độ Oxy, cho \(\vec u = \left( {2;7} \right)\). Kết luận nào sau đây đúng?
A. \(\vec u = 2\vec i - 7\vec j\);
B. \(\vec u = 7\vec i + 2\vec j\);
C. \(\vec u = 2\vec i + 7\vec j\);
D. \(\vec u = - 2\vec i - 7\vec j\).
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow {OA} = \left( {{a_1};{a_2}} \right)\). Khi đó hoành độ và tung độ của \(\overrightarrow {OA} \) lần lượt là:
A. a1 và a2;
B. a2 và a1;
C. \({a_1}\vec i\) và \({a_2}\vec j\);
D. –a1 và –a2.
Trong mặt phẳng tọa độ Oxy, cho \[\vec a = \left( {1;5} \right)\] và \(\vec b = \left( {3u + v;u - 2v} \right)\). Khi đó \(\vec a = \vec b\) khi và chỉ khi:
A. \(\left\{ \begin{array}{l}u = - 1\\v = 2\end{array} \right.\);
B. \(\left\{ \begin{array}{l}u = 1\\v = - 2\end{array} \right.\);
C. \(\left\{ \begin{array}{l}u = 1\\v = 2\end{array} \right.\);
D. \(\left\{ \begin{array}{l}u = - 1\\v = - 2\end{array} \right.\).
Trong mặt phẳng tọa độ Oxy, cho \(\vec x = \left( {10;2} \right),\,\,\vec y = \left( { - 5;8} \right)\). Khi đó \(\vec x.\vec y\) bằng:
A. –34;
B. (–50; 16);
C. –66;
D. 34.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(–1; –2) và N(–3; 2). Tọa độ trung điểm I của đoạn thẳng MN là:
A. I(1; –2);
B. I(2; 2);
C. I(–2; 0);
D. I(–4; 0).
Trong các phát biểu sau, phát biểu nào sau đây đúng?
A. \[\vec a\] được gọi là vectơ chỉ phương của đường thẳng d nếu \(\vec a \ne \vec 0\) và giá của \[\vec a\] song song hoặc trùng với d;
B. \(\vec n\) được gọi là vectơ pháp tuyến của đường thẳng d nếu \(\vec n \ne \vec 0\) và giá của \(\vec n\) vuông góc với d;
C. Nếu \[\vec a\] là một vectơ chỉ phương của đường thẳng d thì \(k\vec a\,\,\,\left( {k \ne 0} \right)\) là một vectơ pháp tuyến của đường thẳng d;
D. Cả A, B đều đúng.
Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 1;
B. 2;
C. 3;
D. Vô số.
Phương trình tổng quát của đường thẳng đi qua hai điểm A(–2; 4) và B(1; 0) là:
A. 4x + 3y + 4 = 0;
B. 4x + 3y – 4 = 0;
C. 4x – 3y + 4 = 0;
D. 4x – 3y – 4 = 0.
Cho điểm M nằm trên ∆: x + y – 1 = 0 và cách N(–1; 3) một khoảng bằng 5. Khi đó tọa độ điểm M là:
A. M(2; –1);
B. M(–2; –1);
C. M(–2; 1);
D. M(2; 1).
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1, d2 lần lượt có vectơ chỉ phương là \({\vec a_1}\), \({\vec a_2}\). Gọi M là một điểm nằm trên đường thẳng d1. Khi đó d1 trùng d2 khi và chỉ khi:
A. \({\vec a_1}\) cùng phương với \({\vec a_2}\);
B. \({\vec a_1}\) không cùng phương với \({\vec a_2}\);
C. M ∈ d2;
D. Cần có cả hai điều kiện của hai phương án A và C.
Góc giữa hai đường thẳng \({\Delta _1}:2x + 2\sqrt 3 y + \sqrt 5 = 0\) và \({\Delta _2}:y - \sqrt 6 = 0\) là:
A. 60°;
B. 125°;
C. 145°;
D. 30°.
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn khi và chỉ khi:
A. a2 + b2 ≥ c;
B. a2 + b2 < c;
C. a2 + b2 > c;
D. a2 + b2 ≤ c.
Một đường tròn có tâm I(3; –2), tiếp xúc với đường thẳng ∆: x – 5y + 1 = 0. Bán kính của đường tròn đó bằng:
A. 6;
A. 6;
C. \(\frac{{14}}{{\sqrt {26} }}\);
D. \(\frac{7}{{13}}\).
Cho đường tròn (C): (x – 3)2 + (y – 1)2 = 10. Phương trình tiếp tuyến của (C) tại điểm A(4; 4) là:
A. x – 3y + 5 = 0;
B. x + 3y – 4 = 0;
C. x – 3y + 16 = 0;
D. x + 3y – 16 = 0.
Phương trình nào sau đây là phương trình chính tắc của elip?
A. \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{{25}} = 1\);
B. \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{12}} = 1\);
C. \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{36}} = 1\);
D. \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{49}} = 1\).
Phương trình chính tắc của parabol (P) có đường chuẩn ∆: 2x + 6 = 0 là:
A. y2 = 24x;
B. y2 = 3x;
C. y2 = 12x;
D. y2 = 6x.
Cho hypebol (H): \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) và đường thẳng ∆: x + y = 3. Tích các khoảng cách từ hai tiêu điểm của (H) đến ∆ bằng giá trị nào sau đây?
A. 16;
B. 8;
C. 64;
D. 7.

