35 CÂU HỎI
Nếu một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện (các cách thực hiện của hai hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là
A. ab;
B. a + b;
C. 1;
D. \(\frac{a}{b}\).
Nếu một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có a cách thực hiện, ứng với mỗi cách thực hiện hành động thứ nhất, có b cách thực hiện hành động thứ hai thì số cách hoàn thành công việc đó là
A. ab;
B. a + b;
C. 1;
D. \(\frac{a}{b}\).
Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.
A. 31;
B. 16;
C. 47;
D. 15.
Các thành phố A; B; C; D được nối với nhau bởi các con đường như hình vẽ sau:
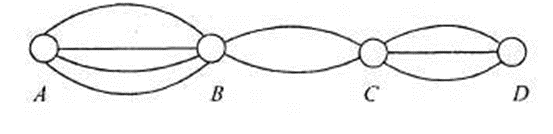
Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
A. 12;
B. 18;
C. 20;
D. 24.
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là
A. n.k;
B. n.(n – 1).(n – 2)…(n – k + 1);
C.\(\frac{n}{k}\);
D.\(\frac{k}{n}\).
Số các hoán vị của n phần tử là
A. n;
B. n + 1;
C. n – 1;
D. n(n – 1). ... . 2 . 1.
Cho tập hợp A gồm n phần tử (n ∈ ℕ*). Mỗi hoán vị của n phần tử đó là
A. Một kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A;
B. Tất cả các kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A;
C. Một số được tính bằng n(n – 1) . ... . 2 . 1;
D. Một số được tính bằng n!.
Ở căn hộ chung cư nhà An người ta thường dùng các chữ số từ 0 đến 9 để thiết lập mật khẩu. Nhà An muốn thiết lập một mật khẩu gồm 4 chữ số khác nhau. Số cách thiết lập mật khẩu cho nhà An là
A. 5 000 cách;
B. 540 cách;
C. 504 cách;
D. 5 040 cách.
Một tổ có 8 học sinh trong đó có một bạn tên Cường và một bạn tên Nam. Số cách sắp xếp 8 học sinh đó thành một hàng sao cho Cường đứng đầu hàng và Nam đứng cuối hàng là
A. 120;
B. 360;
C. 720;
D. 960.
Tổ hợp chập k của n phần tử với 1 ≤ k ≤ n được kí hiệu là
A.\(C_n^k\);
B.\(C_k^n\);
C.\(A_n^k\);
D. \(A_k^n\).
Cho k, n là các số nguyên dương với k ≤ n. Trong các phát biểu dưới đây, phát biểu nào sai?
A. \(C_n^k = C_n^{n - k}\);
B.\(C_n^k = \frac{{A_n^k}}{{\left( {n - k} \right)!}}\);
C.\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\);
D. \(C_n^k = \frac{{A_n^k}}{{k!}}\).
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là 2 trong 8 điểm đó?
A. 28;
B. 30;
C. 56;
D. 58.
Một tổ có 12 học sinh, trong đó có một học sinh tên Châu. Có bao nhiêu cách chọn một nhóm gồm 5 người trong đó có học sinh tên Châu đi làm trực nhật?
A. 110;
B. 495;
C. 330;
D. 792.
Cho biểu thức (a + b)n , với n = 4 ta có khai triển là
A. (a + b)4 = \(C_4^0{a^4} + C_4^1{a^3}{b^1} + C_4^2{a^2}{b^2} + C_4^3a{b^3} + C_4^4{b^4}\);
B. (a + b)4 = \(C_4^0{a^4} - C_4^1{a^3}{b^1} - C_4^2{a^2}{b^2} - C_4^3a{b^3} - C_4^4{b^4}\);
C. (a + b)4 = \(C_4^0{a^4} - C_4^1{a^3}{b^1} + C_4^2{a^2}{b^2} - C_4^3a{b^3} + C_4^4{b^4}\);
D. (a + b)4 = \( - C_4^0{a^4} - C_4^1{a^3}{b^1} - C_4^2{a^2}{b^2} - C_4^3a{b^3} - C_4^4{b^4}\).
Trong các phát biểu sau, phát biểu nào đúng?
A. (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5;
B. (a – b)5 = a5 – 5a4b + 10a3b2 + 10a2b3 – 5ab4 + b5;
C. (a + b)5 = a5 + b5;
D. (a – b)5 = a5 – b5.
Hệ số của x3 của khai triển (x – 1)4 là
A. 1;
B. 4;
C. – 4;
D. 6.
Trong mặt phẳng tọa độ Oxy, cho vectơ \(\overrightarrow a = 3\overrightarrow i - 9\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
A. (1; 3);
B. (1; – 3);
C. (3; – 9);
D. (3; 9).
Trong mặt phẳng tọa độ Oxy, cho M(2; – 1) và N(4; 1). Tọa độ vectơ \(\overrightarrow {NM} \) là
A. (– 2; – 2);
B. (2; 2);
C. (6; 0);
D. (2; – 2).
Cho hình dưới đây.
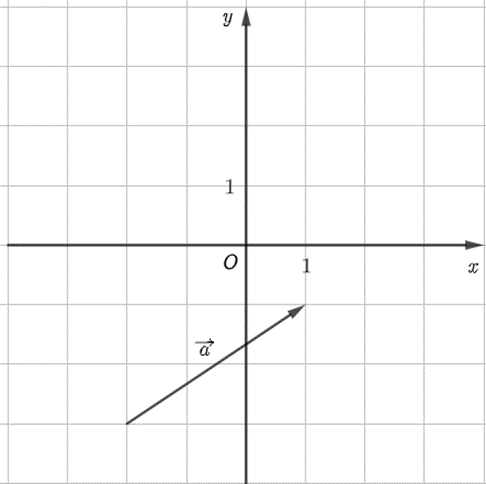
Tọa độ của vectơ \(\overrightarrow a \) trong hình vẽ trên là
A. (1; 1);
B. (3; 2);
C. (1; 2);
D. (2; 1).
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = \left( { - 5;\,\,3} \right),\,\,\overrightarrow v = \left( {2x + y;\,x - y} \right)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu
A. \(\left\{ \begin{array}{l}x = - \frac{2}{3}\\y = - \frac{{11}}{3}\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = \frac{2}{3}\\y = - \frac{{11}}{3}\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = \frac{2}{3}\\y = \frac{{11}}{3}\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = - \frac{2}{3}\\y = \frac{{11}}{3}\end{array} \right.\).
Cho hình bình hành ABCD có A(– 3; 2), B(– 1; 3), C(– 1; 2). Tọa độ của đỉnh D là
A. (3; 1);
B. (1; 3);
C. (– 3; 1);
D. (– 3; – 1).
Trong mặt phẳng tọa độ Oxy, cho A(1; 1) và B(5; – 2). Độ dài đoạn thẳng AB là
A. 5;
B. \(\sqrt {37} \);
C. \(\sqrt {17} \);
D. 25.
Cho ba vectơ \(\overrightarrow x = \left( {1;\, - 2} \right)\), \(\overrightarrow y = \left( {5;\,\,10} \right)\), \(\overrightarrow z = \left( { - \frac{1}{2};\,1} \right)\). Khẳng định nào sau đây là đúng?
A. Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) cùng phương;
B. Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow z \) cùng phương;
C. Hai vectơ \(\overrightarrow y ,\,\,\overrightarrow z \) cùng phương;
D. Không có cặp vectơ nào cùng phương trong ba vectơ trên.
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {2;\,\, - 1} \right)\) và \(\overrightarrow b = \left( {3;\,\,4} \right)\). Tọa độ của vectơ \(\overrightarrow c = \overrightarrow a + 3\overrightarrow b \) là
A. (11; 11);
B. (11; – 13);
C. (11; 13);
D. (7; 13).
Số đo góc giữa hai vectơ \(\overrightarrow x = \left( {1;\,\, - 2} \right)\) và \[\overrightarrow y = \left( { - 2;\,\, - 6} \right)\] bằng
A. 30°;
B. 45°;
C. 60°;
D. 135°.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
A. \(\overrightarrow n = \left( {1;\,\, - 2} \right)\);
B. \(\overrightarrow n = \left( {1;\,\,2} \right)\);
C. \(\overrightarrow n = \left( {2;\,\, - 1} \right)\);
D. \(\overrightarrow n = \left( {2;\,\,1} \right)\).
Điểm nào dưới đây thuộc đường thẳng d: 3x – 2y + 4 = 0?
A. A(1; 2);
B. B(0; 2);
C. C(2; 0);
D. D(2; 1).
Phương trình tham số của đường thẳng ∆ đi qua điểm A(3; 1) và nhận \(\overrightarrow u = \left( {3;\,\, - 1} \right)\) làm vectơ chỉ phương là
A. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 - t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 + t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 + t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 - t\end{array} \right.\).
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng d là
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Cho các điểm A(3; 7) và B(6; 1). Đường thẳng AB có phương trình là
A. 2x + y + 13 = 0;
B. 3x + 7y – 13 = 0;
C. 7x + 3y + 13 = 0;
D. 2x + y – 13 = 0.
Cho hai đường thẳng d1: 2x – 3y + 7 = 0 và d2: 4x – 6y + 10 = 0. Chọn khẳng định đúng trong các khẳng định sau.
A. d1 // d2;
B. d1 ⊥ d2;
C. d1 và d2 trùng nhau;
D. d1 và d2 cắt nhau nhưng không vuông góc.
Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
A. 13;
B. – 13;
C. – 1;
D. 1.
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆1 và ∆2 có vectơ pháp tuyến lần lượt là \({\vec n_1},\,\,{\vec n_2}\). Nếu \({\vec n_1}.{\vec n_2} = 0\) thì:
A. ∆1 // ∆2;
B. ∆1 trùng ∆2;
C. ∆1 ⊥ ∆2;
D. ∆1 cắt ∆2 nhưng không vuông góc với ∆2.
Cho đường thẳng d: x – 2y + 1 = 0. Nếu đường thẳng ∆ đi qua điểm M(1; – 1) và ∆ song song với d thì ∆ có phương trình:
A. x – 2y – 3 = 0;
B. x – 2y + 5 = 0;
C. x – 2y + 3 = 0;
D. x + 2y + 1 = 0.
Góc giữa hai đường thẳng a: \(\sqrt 3 \)x – y + 7 = 0 và b: x – \(\sqrt 3 \)y – 2 = 0 là
A. 30°;
B. 90°;
C. 60°;
D. 45°.

