35 CÂU HỎI
Nếu một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện, hành động thứ ba có k cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là
A. mnk;
B. m + n + k;
C. 1;
D. mn + k.
Nếu một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện, ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai, ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động số hai, có k cách thực hiện hành động số ba thì số cách hoàn thành công việc đó là
A. mnk;
B. m + n + k;
C. 1;
D. mn + k.
Cho tập A = {0; 1; 3; 5; 7}. Có thể lập được bao nhiêu số tự nhiên có 4 chữ số sao cho các chữ số đó đôi một khác nhau và là số chẵn.
A. 32;
B. 12;
C. 24;
D. 96.
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
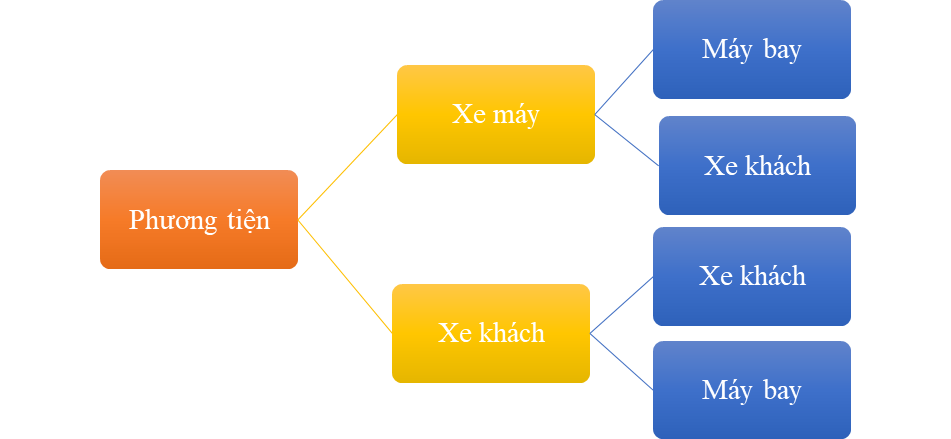
Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
A. 3;
B. 4;
C. 5;
D. 6.
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Mỗi chỉnh hợp chập k của n phần tử đã cho là
A. Một kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A;
B. Tất cả các kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó;
C. Một kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó;
D. Một số được tính bằng n(n – 1) ... (n – k + 1).
Số các hoán vị của 5 phần tử là
A. 5;
B. \(A_5^1\);
C. 10;
D. 5!.
Cho k, n là các số nguyên dương, k ≤ n. Trong các phát biểu sau, phát biểu nào sai?
A. \[A_n^k = n\left( {n - 1} \right)....\left( {n - k + 1} \right)\];
B. Pn = n(n – 1) ... 2 . 1;
C. Pn = n!;
D. \(A_n^k = \frac{{n!}}{{k!}}\).
Có bao nhiêu cách xếp 5 người ngồi vào một dãy ghế gồm có 6 chiếc ghế, biết mỗi người ngồi vào một ghế.
A. 30;
B. 11;
C. 38;
D. 720.
Sắp xếp năm bạn học sinh Anh, Chánh, Châu, Hằng, Loan vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Châu luôn ngồi chính giữa là
A. 24;
B. 120;
C. 60;
D. 16.
Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
A.\(C_6^3\);
B. {1; 5; 9};
C. 6!;
D. \(A_6^3\).
Với n là số nguyên dương tùy ý lớn hơn 1, mệnh đề nào dưới đây đúng?
A. \(C_n^2 = n\left( {n - 1} \right)\);
B.\(C_n^2 = \frac{{n\left( {n - 1} \right)}}{2}\);
C.\(C_n^2 = 2n\);
D. \[C_n^2 = \frac{{n!\left( {n - 1} \right)!}}{2}\].
Một lớp có 40 học sinh gồm 25 nam và 15 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh trong đó có ít nhất một học sinh nữ?
A. 7580;
B. 7125;
C. 455;
D. 544.
Trong một hộp đựng 4 viên bi hồng và 3 viên bi tím. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên bi cùng màu?
A. 4;
B. 18;
C. 9;
D. 22.
Cho biểu thức (a + b)n , với n = 4 thì khi khai triển ta được một biểu thức có số số hạng là
A. 4;
B. 5;
C. 6;
D. 8.
Trong các phát biểu sau, phát biểu nào đúng?
A. (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5;
B. (a – b)5 = a5 – 5a4b + 10a3b2 + 10a2b3 – 5ab4 + b5;
C. (a + b)5 = a5 + b5;
D. (a – b)5 = a5 – b5.
Số hạng không chứa x trong khai triển nhị thức Newton của (2x – 5)5 là
A. 1;
B. 32;
C. – 3125;
D. 6250.
Trong mặt phẳng tọa độ Oxy, cho vectơ \(\overrightarrow a = - 2\overrightarrow i + 3\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
A. (– 2; – 3);
B. (2; – 3);
C. (– 2; 3);
D. (2; 3).
Trong mặt phẳng tọa độ Oxy, cho M(3; – 6) và N(5; 2). Tọa độ trung điểm I của MN là
A. (4; – 2);
B. (1; 4);
C. (2; – 8);
D. (2; – 2).
Trong mặt phẳng tọa độ Oxy, cho điểm H(1; 6). Tọa độ của vectơ \(\overrightarrow {OH} \) là
A. (6; 1);
B. (3; 2);
C. (1; 6);
D. (7; 0).
Tìm các số thực a và b để cặp vectơ sau bằng nhau \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;\,4b} \right)\).
A. a = 2, b = 1;
B. a = 1, b = – 2;
C. a = – 1, b = 2;
D. a = – 2, b = 1.
Cho hình bình hành ABCD có A(– 1; – 2), B(3; 2), C(4; – 1). Tọa độ của đỉnh D là
A. (8; 3);
B. (3; 8);
C. (– 5; 0);
D. (0; – 5).
Trong mặt phẳng tọa độ Oxy, cho A(2; 7) và B(– 2; 8). Độ dài đoạn thẳng AB là
A. 5;
B. \(\sqrt {37} \);
C. \(\sqrt {17} \);
D. 25.
Cho hai vectơ \(\overrightarrow x = \left( {3;\, - 4} \right)\), \(\overrightarrow y = \left( { - 6;\,\,8} \right)\). Khẳng định nào sau đây là đúng?
A. Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) bằng nhau;
B. Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) cùng phương cùng hướng;
C. Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) cùng phương ngược hướng;
D. Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) đối nhau.
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {4;\,\, - m} \right)\) và \(\overrightarrow b = \left( {2m + 6;\,\,1} \right)\). Tập giá trị của m để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương là
A. {– 1; 1};
B. {– 1; 2};
C. {– 2; – 1};
D. {– 2; 1}.
Cho tam giác ABC có A(1; 2), B(– 1; 1), C(5; – 1). Tính \(\overrightarrow {AB} \cdot \overrightarrow {AC} \).
A. 7;
B. – 5;
C. 5;
D. – 7.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
A. \(\overrightarrow n = \left( {1;\,\, - 2} \right)\);
B. \(\overrightarrow n = \left( { - 1;\,\,2} \right)\);
C. \(\overrightarrow n = \left( {2;\,\, - 1} \right)\);
D. \(\overrightarrow n = \left( {2;\,\,1} \right)\).
Phương trình tham số của đường thẳng ∆ đi qua điểm A(– 4; 2) và nhận \(\overrightarrow u = \left( {2;\,\, - 5} \right)\) làm vectơ chỉ phương là
A. \(\left\{ \begin{array}{l}x = 2 - 4t\\y = - 5 + 2t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = - 4 + 2t\\y = 2 - 5t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 5 + t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = - 4 + 2t\\y = 2 + 5t\end{array} \right.\).
Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận \(\overrightarrow n = \left( { - 2;\,\,7} \right)\) làm vectơ pháp tuyến là
A. 2x – 7y + 23 = 0;
B. – 2x + 7y – 23 = 0;
C. 2x – 7y – 23 = 0;
D. – 2x – 7y + 23 = 0.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
A. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 - t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 + t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = - 3t\\y = t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = - 6 - 3t\\y = 2 + t\end{array} \right.\).
Cho đường thẳng ∆ đi qua điểm A(4; – 5) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\,2} \right)\). Phương trình tham số của đường thẳng ∆ là
A. \(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 5 - t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = 4 + t\\y = - 5 + 2t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = 1 + 4t\\y = 2 - 5t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 2 + 4t\\y = - 1 - 5t\end{array} \right.\).
Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
A. \(2\sqrt {13} \);
B. \(\frac{{28}}{{\sqrt {13} }}\);
C. 26;
D. \(\frac{{\sqrt {13} }}{2}\).
Góc giữa hai đường thẳng a: 6x – 5y + 15 = 0 và b: \(\left\{ \begin{array}{l}x = 10 - 6t\\y = 1 + 5t\end{array} \right.\) bằng
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
A. 2x + 3y – 8 = 0;
B. 2x + 3y + 8 = 0;
C. 3x – 2y + 1 = 0;
D. 2x + 3y – 2 = 0.
Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
A. \(\left( {\frac{{27}}{{13}};\, - \frac{{17}}{{13}}} \right)\);
B. (– 27; 17);
C. (27; – 17);
D. \(\left( { - \frac{{27}}{{13}};\,\frac{{17}}{{13}}} \right)\).
Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\) và d2: mx + 2y – 14 = 0. Giá trị của m để hai đường thẳng trên song song với nhau là
A. m = 1;
B. m = – 2;
C. m ∈ {– 2; 1};
D. Không có giá trị nào của m thỏa mãn.

