12 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Hãng hàng không Quốc gia VietNam Airlines khai thác duy nhất một chuyến bay từ Đà Nẵng đi Đà Lạt vào ngày 30 tháng 4 với các loại vé khác nhau được mô tả bởi sơ đồ hình cây sau:
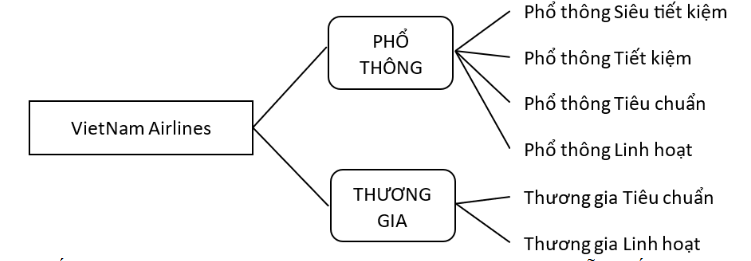
Một người muốn mua vé của hãng máy bay VietNam Airlines đi từ Đà Nẵng đến Đà Lạt vào ngày 30 tháng 4. Hỏi có bao nhiêu loại vé để người đó lựa chọn?
A. 2.
B. 6.
C. 9.
D. 8.
Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
A. \({5^5}\).
B. \(5!\).
C. \(4!\).
D. \(5\).
Tập \(A\) gồm \(n\) phần tử (\(n > 0\)). Hỏi \(A\) có bao nhiêu tập con?
A. \(A_n^2\).
B. \(C_n^2\).
C. \({2^n}\).
D. \({3^n}\).
Chọn công thức đúng
A. \({\left( {a + b} \right)^4} = {a^4} - 4{a^3}b - 6{a^2}{b^2} - 4a{b^3} - {b^4}\).
B. \({\left( {a + b} \right)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\).
C. \({\left( {a + b} \right)^4} = {a^4} + 4{a^3}b - 6{a^2}{b^2} + 4a{b^3} + {b^4}\).
D. \({\left( {a + b} \right)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\).
Một thí nghiệm hay một hành động mà ta không thể biết trước được kết quả của nó thì gọi là
A. Xác suất.
B. Phép thử.
C. Không gian mẫu.
D. Biến cố.
Xét \(A\) là biến cố liên quan đến phép thử T với không gian mẫu là \(\Omega \). Mệnh đề nào dưới đây sai?
A. \(P\left( \emptyset \right) = 0\).
B. \(0 < P\left( A \right) < 1\).
</>
C. \(P\left( \Omega \right) = 1\).
D. \(P\left( A \right) + P\left( {\overline A } \right) = 1\).
Đường thẳng đi qua \(M\left( {3; - 1} \right)\) và nhận vectơ \(\overrightarrow u = \left( { - 2;5} \right)\) làm vectơ chỉ phương có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = 3 - 2t\\y = - 1 + 5t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 3 - 2t\\y = - 1 - 5t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 3 + 5t\\y = - 1 + 2t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 5 - t\end{array} \right.\).
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục \(Ox\).
A. \(\overrightarrow u = \left( {1;0} \right)\).
B. \(\overrightarrow u = \left( {1; - 1} \right)\).
C. \(\overrightarrow u = \left( {1;1} \right)\).
D. \(\overrightarrow u = \left( {0;1} \right)\).
Trong mặt phẳng \(Oxy\), phương trình nào sau đây là phương trình của đường tròn?
A. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
B. \({x^2} + {y^2} - 4x + 6y - 12 = 0\).
C. \({x^2} + {y^2} - 2x - 8y + 20 = 0\).
D. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
Cho một đường thẳng \(\Delta \) và một điểm \(F\) không thuộc \(\Delta \). Tập hợp các điểm \(M\) sao cho \(MF = d\left( {M,\Delta } \right)\) là
A. một elip.
B. một parabol.
C. một hypebol.
D. một đường tròn.
Tính số chỉnh hợp chập 4 của 7 phần tử?
A. \(35\).
B. \(720\).
C. \(24\).
D. \(840\).
Khai triển nhị thức \({\left( {2{x^2} - \frac{1}{2}} \right)^5}\) ta được số hạng chứa \({x^6}\) là:
A. \( - \frac{5}{8}\).
B. \(20{x^6}\).
C. \( - 20\).
D. \(\frac{5}{8}{x^6}\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải