13 CÂU HỎI
Cho hàm số \(y = f\left( x \right)\) có bảng giá trị sau:
Hàm số \(y = f\left( x \right)\) là hàm số nào sau đây?
A. \(y = {x^2}\).
B. \(y = - {x^2}\).
C. \(y = 2x\).
D. \(y = - 2x\).
Cho parabol \(\left( P \right):y = 3{x^2} - 2x + 1\). Điểm nào sau đây thuộc \(\left( P \right)\).
A. \(A\left( {0; - 1} \right)\).
B. \(B\left( { - \frac{1}{3};\frac{2}{3}} \right)\).
C. \(I\left( {1;2} \right)\).
D. \(C\left( {\frac{1}{3}; - \frac{2}{3}} \right)\).
Cho tam thức bậc hai \(f\left( x \right) = - {x^2} + 6x - 5\) có bảng xét dấu như sau:
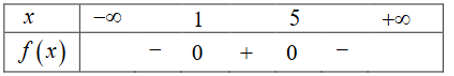
Mệnh đề nào sau đây đúng?
A.\(f\left( x \right) > 0,\forall x \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
B. \(f\left( x \right) < 0,\forall x \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
C. \(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
D. \(f\left( x \right) < 0,\forall x \in \left( {1;5} \right)\).
Kết quả nào dưới đây không phải là nghiệm của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \)?
A. \(x = 0\).
B. \(x = 0\)và \(x = - \frac{3}{5}\).
C. \(x = \frac{3}{5}\).
D. \(x = - \frac{3}{5}\).
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = - 2t\\y = 4 + t\end{array} \right.\). Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của \(d\)?
A. \(\overrightarrow {{n_1}} = \left( {1; - 2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( { - 2;1} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {3;6} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {4;2} \right)\).
Đường thẳng nào sau đây song song với đường thẳng \(\Delta :2x + 3y - 1 = 0\)?
A. \(x - 2y + 5 = 0\).
B. \(2x + 3y + 1 = 0\).
C. \(2x - 3y + 3 = 0\).
D. \(4x - 6y - 2 = 0\).
Tìmtọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} = 8\).
A. \(I\left( { - 1;3} \right),R = 8\).
B. \(I\left( {1; - 3} \right),R = 8\).
C. \(I\left( { - 1;3} \right),R = 2\sqrt 2 \).
D. \(I\left( {1; - 3} \right),R = 2\sqrt 2 \).
Tìmtọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} = 8\).
A. \(I\left( { - 1;3} \right),R = 8\).
B. \(I\left( {1; - 3} \right),R = 8\).
C. \(I\left( { - 1;3} \right),R = 2\sqrt 2 \).
D. \(I\left( {1; - 3} \right),R = 2\sqrt 2 \).
Phương trình nào sau đây là phương trình chính tắc của đường hypebol?
A. \(\frac{{{x^2}}}{3} - \frac{{{y^2}}}{4} = 1\).
B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{6} = 1\).
C. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{16}} = 0\).
D. \(\frac{{{y^2}}}{{16}} - \frac{{{x^2}}}{9} = 1\).
Parabol dưới đây là đồ thị của hàm số nào?
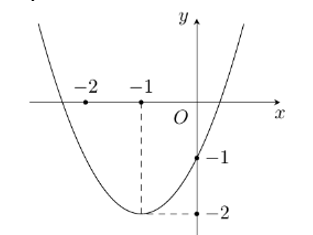
A. \(y = {x^2} + 2x - 1\).
B. \(y = {x^2} + 2x - 2\).
C. \(y = - {x^2} - 2x + 1\).
D. \(y = {x^2} - 2x - 1\).
Cho đồ thị của hàm số bậc hai \(y = f\left( x \right)\) như hình vẽ
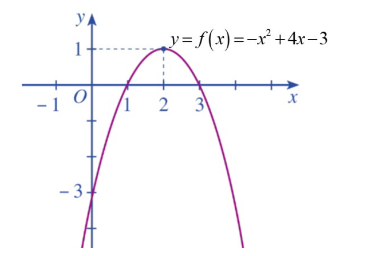
A. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\).
B. \(f\left( x \right) > 0 \Leftrightarrow x \in \left[ {1;3} \right]\).
C. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( {1;3} \right)\).
D. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\).
Tìm \(m\) để 2 đường thẳng \({\Delta _1}:2x - y + 1 = 0\) và \({\Delta _2}:4x - my + 7 = 0\) vuông góc với nhau?
A. \(m = 2\).
B. \(m = - 2\).
C. \(m = - 8\).
D. \(m = 8\).
Trong mặt phẳng \(Oxy\), đường tròn tâm \(I\left( { - 1;2} \right)\) và đi qua điểm \(M\left( {2;1} \right)\) có phương trình là:
A. \({x^2} + {y^2} + 2x - 4y - 5 = 0\).
B. \({x^2} + {y^2} + 2x - 4y - 3 = 0\).
C. \({x^2} + {y^2} - 2x - 4y - 5 = 0\).
D. \({x^2} + {y^2} + 2x + 4y - 5 = 0\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
