11 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 11.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Với \(a\) là số thực dương tùy ý, \(\sqrt[{14}]{a}\) bằng
A. \({a^{\frac{1}{{14}}}}\).
B. \({a^{\sqrt {14} }}\).
C. \({a^{14}}\).
D. \(\sqrt {{a^{14}}} \).
Cho \(a,b\) là các số thực dương tùy ý. Khẳng định nào sau đây là đúng?
A. \(\ln \left( {a + b} \right) = \ln a.\ln b\).
B. \(\ln \left( {a + b} \right) = \ln a + \ln b\).
C. \(\ln \left( {ab} \right) = \ln a + \ln b\).
D. \(\ln \left( {ab} \right) = \ln a.\ln b\).
Nghiệm của phương trình \({3^x} = 1\) là
A. \(x = 2\).
B. \(x = - 1\).
C. \(x = 0\).
D. \(x = 1\).
Với hai số thực dương \(a,b\) tùy ý và \(\frac{{{{\log }_3}5.{{\log }_5}a}}{{1 + {{\log }_3}2}} - {\log _6}b = 2\). Khẳng định nào dưới đây là khẳng định đúng?
A. \(a = 36b\).
B. \(a = b{\log _6}3\).
C. \(2a + 3b = 0\).
D. \(a = b{\log _6}2\).
Có bao nhiêu số nguyên thuộc tập xác định của hàm số \(y = \log \left[ {\left( {6 - x} \right)\left( {x + 2} \right)} \right]\)?
A. \(7\).
B. \(8\).
C. Vô số.
D. \(9\).
Cho \({4^x} + {4^{ - x}} = 7\). Biểu thức \(P = \frac{{5 + {2^x} + {2^{ - x}}}}{{8 - {{4.2}^x} - {{4.2}^{ - x}}}}\) có giá trị bằng
A. \(P = \frac{3}{2}\).
B. \(P = - \frac{5}{2}\).
C. \(P = 2\).
D. \(P = - 2\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông. Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SC\).
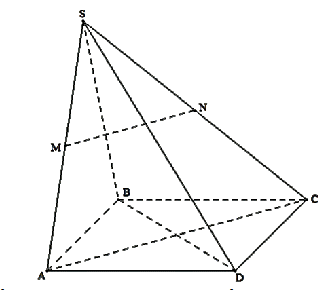
Chọn khẳng định đúng trong các khẳng định sau:
A. \(MN \bot BD\).
B. \(MN \bot SD\).
C. \(MN \bot SA\).
D. \(MN \bot SB\).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\) và \(SA \bot \left( {ABC} \right)\).
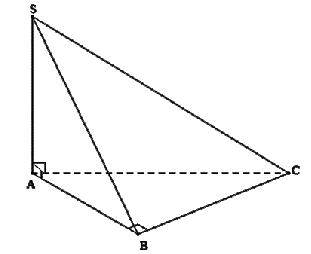
Hình chiếu của \(SC\) lên \(\left( {ABC} \right)\) là
A. \(SB\).
B. \(BC\).
C. \(AB\).
D. \(AC\).
Trong các mệnh đề dưới đây, mệnh đề nào là đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Cho tứ diện đều \(ABCD\) có tất cả các cạnh đều bằng \(a\). Tính cosin góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {BCD} \right)\).
A. \(\cos \alpha = \frac{1}{6}\).
B. \(\cos \alpha = \frac{1}{3}\).
C. \(\cos \alpha = \frac{1}{4}\).
D. \(\cos \alpha = \frac{1}{2}\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Đường thẳng \(AC'\) vuông góc với mặt phẳng nào sau đây?
A. \(AC' \bot \left( {BB'D'D} \right)\).
B. \(AC' \bot \left( {ABCD} \right)\).
C. \(AC' \bot \left( {AA'D'D} \right)\).
D. \(AC' \bot \left( {A'BD} \right)\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
