12 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Rút gọn biểu thức \(P = {x^{\frac{1}{3}}}.\sqrt[6]{x}\) với \(x > 0\).
A. \(P = \sqrt x \).
B. \(P = {x^{\frac{1}{3}}}\).
C. \(P = {x^{\frac{1}{9}}}\).
D. \(P = {x^2}\).
Với \(a,b,x\) là các số thực dương thỏa mãn \({\log _2}x = 5{\log _2}a + 3{\log _2}b\), mệnh đề nào dưới đây đúng?
A. \(x = 3a + 5b\).
B. \(x = 5a + 3b\).
C. \(x = {a^5} + {b^3}\).
D. \(x = {a^5}{b^3}\).
Trong các hàm số sau, hàm số nào sau đây là hàm số mũ?
A. \(y = {x^2}\).
B. \(y = {2^x}\).
C. \(y = {x^\pi }\).
D. \(y = \sqrt x \).
Tập nghiệm \(S\) của bất phương trình \({\log _2}x > 2\) là:
A. \(S = \left( {2; + \infty } \right)\).
B. \(S = \left( {0;2} \right)\).
C. \(S = \left( {0;4} \right)\).
D. \(S = \left( {4; + \infty } \right)\).
Giá trị của biểu thức \(A = \frac{{{6^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }}{{.3}^{1 + \sqrt 5 }}}}\) bằng
A. \({6^{ - \sqrt 5 }}\).
B. \(18\).
C. \(1\).
D. \(9\).
Tìm \(a\) để hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình bên
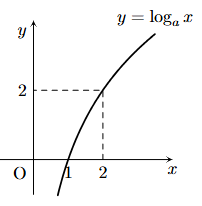
A. \(a = \sqrt 2 \).
B. \(a = \frac{1}{{\sqrt 2 }}\).
C. \(a = \frac{1}{2}\).
D. \(a = 2\).
Mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
B. Hai đường thẳng cùng vuông góc gới một đường thẳng thì song song với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
Trong không gian mặt phẳng \(\left( P \right)\) và đường thẳng \(d\) không vuông góc với mặt phẳng \(\left( P \right)\). Hãy chọn mệnh đề phát biểu đúng trong các mệnh đề dưới đây?
A. Tồn tại duy nhất một mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(d\) và \(\left( \alpha \right)\) song song với \(\left( P \right)\).
B. Không tồn tại mặt phẳng \(\left( \alpha \right)\)chứa đường thẳng \(d\) và \(\left( \alpha \right)\) song song với \(\left( P \right)\).
C. Tồn tại duy nhất một mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(d\) và \(\left( \alpha \right)\) vuông góc với \(\left( P \right)\).
D. Tồn tại duy nhất một đường thẳng \(\Delta \) nằm trên mặt phẳng \(\left( P \right)\) và \(\Delta \) vuông góc với \(d\).
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không vuông góc với nhau. Gọi \(a'\) là hình chiếu vuông góc của \(a\) lên mặt phẳng \(\left( P \right)\). Giả sử \(b\) là một đường thẳng nằm trong mặt phẳng \(\left( P \right)\) và \(b \bot a'\).
Khi đó
A. Đường thẳng \(a\) luôn luôn chéo \(b\).
B. Đường thẳng \(a\) luôn luôn cắt \(b\).
C. \(a//b\).
D. \(a \bot b\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), đáy \(ABC\) là tam giác vuông tại \(A\), \(M\) là trung điểm \(BC\). Khi đó mặt phẳng \(\left( {ABC} \right)\) không vuông góc với mặt phẳng nào?
A. \(\left( {SAB} \right)\).
B. \(\left( {SAM} \right)\).
C. \(\left( {SAC} \right)\).
D. \(\left( {SBC} \right)\).
Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) được gọi là vuông góc với nhau nếu:
A. góc giữa chúng bằng \(90^\circ \).
B. góc giữa chúng bằng \(180^\circ \).
C. góc giữa chúng bằng \(0^\circ \).
D. góc giữa chúng bằng \(45^\circ \).
Cho hình chóp đều \(S.ABCD\). Gọi \(I\) là trung điểm của \(AB\), \(G\) là trọng tâm của tam giác \(SCD\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\left( {SAC} \right) \bot \left( {SAD} \right)\).
B. \(\left( {SAB} \right) \bot \left( {SIG} \right)\).
C. \(\left( {SIG} \right) \bot \left( {SBC} \right)\).
D. \(\left( {SAD} \right) \bot \left( {SBD} \right)\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải