50 CÂU HỎI
Trong không gian Oxyz,cho đường thẳng \[d:\frac{{x - 2}}{2} = \frac{{y + 3}}{1} = \frac{{z - 1}}{{ - 2}}.\] Vectơ nào dưới đây là một vectơ chỉ phương của d?
A.\[\vec u = \left( {2;3;1} \right).\]
B.\[\vec u = \left( {2;1; - 2} \right).\]
C.\[\vec u = \left( {2; - 3;1} \right).\]
D.\[\vec u = \left( {2;1;2} \right).\]
Cho hàm số f(x) có bảng biến thiên như sau:
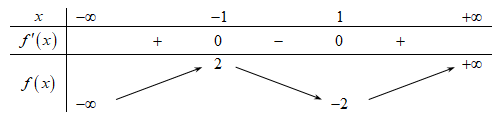
Giá trị cực tiểu của hàm số đã cho là
A.2.
B.−1.
C.−2.
D.1.
Cho hàm số f(x) có bảng biến thiên như sau:
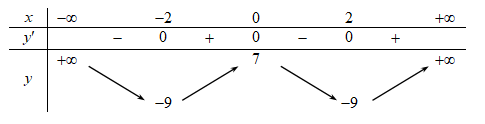
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.\[\left( { - 2;0} \right).\]
B.\[\left( { - \infty ; - 2} \right).\]
C.\[\left( {2; + \infty } \right).\]
D.\[\left( { - 2; + \infty } \right).\]
Trong không gian Oxyz,cho mặt phẳng \[\left( P \right):x - 6y + 12 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\[\vec n = \left( {1; - 6;0} \right).\]
B.\[\vec n = \left( {1; - 6;12} \right).\]
C.\[\vec n = \left( {1;0; - 6} \right).\]
D.\[\vec n = \left( {1;6;0} \right).\]
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
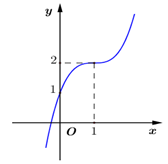
A.\[y = {x^3} - 3{x^2} + 3x + 1.\]
B.\[y = - {x^3} + 3{x^2} + 1.\]
C.\[y = {x^3} - 3x + 4.\]
D.\[y = - {x^3} - 3{x^2} - 1.\]
Tìm phần thực của số phức z thỏa mãn \[z\left( {1 + i} \right) - 2i = 1.\]
A.\[ - \frac{3}{2}.\]
B.\[\frac{3}{2}.\]
C.\[ - \frac{1}{2}.\]
D.\[\frac{1}{2}.\]
Giới hạn \[\mathop {\lim }\limits_{x \to 1} {\mkern 1mu} \frac{{x + 2}}{{2{x^2} + 1}}\] bằng
A.0.
B.1.
C.\[ + \infty .\]
D.\[ - \infty .\]
Cho hàm số f(x) có bảng biến thiên như sau:
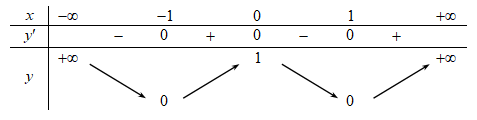
Phương trình \[4f\left( x \right) - 1 = 0\] có số nghiệm thực là
A.1.
B.2.
C.3.
D.4.
Cho hai số thực dương a và b, với \[a \ne 1.\] Mệnh đề nào dưới đây là đúng?
A.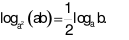
B.![]()
C.![]()
D.
Tích phân \[\int\limits_0^{\frac{\pi }{{12}}} {\sin 3xdx} \] bằng
A.\[\frac{{2 + \sqrt 2 }}{6}.\]
B.\[\frac{{2 - \sqrt 2 }}{6}.\]
C.\[\frac{{2 + \sqrt 2 }}{2}.\]
D.\[\frac{{2 - \sqrt 2 }}{2}.\]
Tính \[P = \frac{1}{{{{\log }_2}2020!}} + \frac{1}{{{{\log }_3}2020!}} + \frac{1}{{{{\log }_4}2020!}} + .... + \frac{1}{{{{\log }_{2020}}2020!}}.\]
A.\[P = 2020.\]
B.\[P = 2020!.\]
C.\[P = \frac{1}{{2020}}.\]
D.\[P = 1.\]
Cho khối nón (N) có đường cao bằng 4 và thể tích bằng 12π. Tính diện tích xung quanh \[{S_{xq}}\] của \[\left( N \right).\]
A.\[{S_{xq}} = 20\pi .\]
B.\[{S_{xq}} = 3\pi \sqrt 7 .\]
C.\[{S_{xq}} = 15\pi .\]
D.\[{S_{xq}} = 12\pi .\]
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
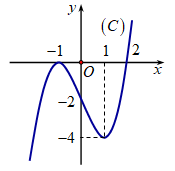
A.\[S = \int\limits_{ - 1}^2 {f\left( x \right)dx} .\]
B.\[S = \int\limits_{ - 1}^0 {f\left( x \right)dx} - \int\limits_0^2 {f\left( x \right)dx} .\]
C.\[S = - \int\limits_{ - 1}^2 {f\left( x \right)dx} .\]
D.\[S = - \int\limits_{ - 1}^0 {f\left( x \right)dx} + \int\limits_0^2 {f\left( x \right)dx} .\]
Tính đạo hàm của hàm số \[y = \ln \left( {1 + \sqrt {2x + 1} } \right).\]
A.\[y' = \frac{1}{{2x + 1 + \sqrt {2x + 1} }}.\]
B.\[y' = \frac{2}{{2x + 1 + \sqrt {2x + 1} }}.\]
C.\[y' = \frac{{\sqrt {2x + 1} }}{{2x + 1 + \sqrt {2x + 1} }}.\]
D.\[y' = \frac{{2\sqrt {2x + 1} }}{{2x + 1 + \sqrt {2x + 1} }}.\]
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = \sin \left( {x + 2} \right)\] là
A.
B.
C.
D.
Cho phương trình phức \[{z^2} - bz + c = 0\] (\[b,{\rm{ }}c \in \mathbb{R}\]) có một nghiệm \[z = 3 + i.\] Tính \[b + c.\]
A.16.
B.4.
C.\[ - 16.\]
D.\[ - 4.\]
Tìm giá trị nhỏ nhất của hàm số \[y = 3x + \frac{4}{{{x^2}}}\] trên khoảng \[\left( {0; + \infty } \right).\]
A.\[3\sqrt[3]{9}.\]
B.7.
C.\[2\sqrt[3]{9}.\]
D.1.
Giải phương trình \[{2^{x + 4}} + {2^{x + 2}} = {5^{x + 1}} + {4.5^x}.\]
A.\[x = {\log _{\frac{2}{5}}}\frac{9}{{20}}.\]
B.\[x = {\log _{\frac{2}{5}}}\frac{{20}}{9}.\]
C.\[x = {\log _{\frac{5}{2}}}\frac{9}{{20}}.\]
D.\[x = {\log _{\frac{5}{2}}}\frac{{20}}{9}.\]
Trong không gian Oxyz,cho hai mặt phẳng \[\left( P \right):2x - 3y + 4z + 6 = 0\] và \[\left( Q \right):2x + 3y - 4z + 5 = 0.\] Kí hiệu α là góc giữa (P) và (Q). Tính \[P = \cos \alpha .\]
A.\[P = \frac{7}{{18}}.\]
B.\[P = \frac{{20}}{{29}}.\]
C.\[P = \frac{9}{{29}}.\]
D.\[P = \frac{{21}}{{29}}.\]
Trong không gian Oxyz,cho hai điểm \[A\left( {1; - 3;2} \right),{\rm{ }}B\left( {2; - 2;3} \right).\] Tìm tọa độ điểm K đối xứng với A qua B.
A.\[K\left( {1;1;1} \right).\]
B.\[K\left( {5; - 3;7} \right).\]
C.\[K\left( {6; - 2;8} \right).\]
D.\[K\left( {3; - 1;4} \right).\]
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn \[\left| {z - 1 + 4i} \right| = 2.\]
A.Đường tròn có tâm \[I\left( { - 1;4} \right)\] và bán kính \[R = 2.\]
B.Đường tròn có tâm \[I\left( { - 1;4} \right)\] và bán kính \[R = 4.\]
C.Đường tròn có tâm \[I\left( {1; - 4} \right)\] và bán kính \[R = 2.\]
D.Đường tròn có tâm \[I\left( {1; - 4} \right)\] và bán kính \[R = 4.\]
Biết \[M\left( {1;0} \right),{\rm{ }}N\left( {0;1} \right)\] là hai điểm cực trị của đồ thị hàm số \[y = a{x^4} + b{x^2} + c.\] Tính giá trị của hàm số tại \[x = 3.\]
A.52.
B.54.
C.64.
D.68.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp S.ABC bằng
A.\[\frac{{{a^3}\sqrt 3 }}{{12}}.\]
B.\[\frac{{{a^3}\sqrt 3 }}{{24}}.\]
C.\[\frac{{{a^3}}}{{12}}.\]
D.\[\frac{{{a^3}}}{{24}}.\]
Giải phương trình \[{\log _2}\left( {x + 12} \right).{\log _x}2 = 2.\]
A.\[x = 2.\]
B.\[x = 4.\]
C.\[x = 6.\]
D.\[x = 8.\]
Cho \[F\left( x \right) = \left( {a{x^2} + bx + c} \right){e^{ - x}}\] là một nguyên hàm của hàm số \[f\left( x \right) = \left( {2{x^2} - 5x + 2} \right){e^{ - x}}\]. Giá trị của \[f\left[ {F\left( 0 \right)} \right]\] bằng
A.\[ - {e^{ - 1}}\]
B.\[20{e^2}\]
C.\[9e\]
D.\[3e\]
Cho hình thang \[ABCD\] có \[\widehat {BAD} = \widehat {ADC} = 90^\circ \] và \[AB = 8,{\rm{ }}CD = BC = 5.\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình thang \[ABCD\] xung quanh trục \[AB.\]
A.\[V = \frac{{128\pi }}{3}.\]
B.\[V = 128\pi .\]
C.\[V = \frac{{256\pi }}{3}.\]
D.\[V = 96\pi .\]
Cho lăng trụ \[ABC.A'B'C'\] có khoảng cách giữa đường thẳng \[CC'\] và mặt phẳng \[\left( {ABB'A'} \right)\] bằng 7. Mặt bên \[ABB'A'\] có diện tích bằng 4. Thể tích của khối lăng trụ \[ABC.A'B'C'\] bằng
A.\[\frac{{28}}{3}.\]
B.28.
C.\[\frac{{14}}{3}.\]
D.14.
Cho số phức \[z = a + bi\] \[\left( {a,{\rm{ }}b \in \mathbb{R}} \right)\] thỏa mãn \[\left| {z + 1} \right| = \left| {z + 5} \right| = 2\sqrt 5 \]. Tính giá trị của biểu thức \[P = a + {b^2}.\]
A.\[P = 1.\]
B.\[P = - 1.\]
C.\[P = 13.\]
D.\[P = 19.\]
Cho hàm số \[y = \frac{{2x - 1}}{{x - 1}}\] có đồ thị (C). Điểm \[M\left( {a;b} \right){\rm{ }}\left( {a >0} \right)\] thuộc (C) sao cho khoảng cách từ M tới tiệm cận đứng của (C) bằng khoảng cách M tới tiệm cận ngang của (C). Mệnh đề nào dưới đây là đúng?
A.\[a + b = \frac{{11}}{2}.\]
B.\[a + b = \frac{{19}}{3}.\]
C.\[a + b = 1.\]
D.\[a + b = 5.\]
Trong không gian \[Oxyz\], cho điểm \[M\left( {1;0;1} \right)\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{{z - 3}}{3}\]. Đường thẳng đi qua M, vuông góc với dvà cắt Oz có phương trình là
A.\[\left\{ {\begin{array}{*{20}{l}}{x = 1 - 3t}\\{y = 0}\\{z = 1 + t}\end{array}} \right..\]
B.\[\left\{ {\begin{array}{*{20}{l}}{x = 1 - 3t}\\{y = 0}\\{z = 1 - t}\end{array}} \right..\]
C.\[\left\{ {\begin{array}{*{20}{l}}{x = 1 - 3t}\\{y = t}\\{z = 1 + t}\end{array}} \right..\]
D.\[\left\{ {\begin{array}{*{20}{l}}{x = 1 + 3t}\\{y = 0}\\{z = 1 + t}\end{array}} \right..\]
Trong không gian, cho hình trụ có thiết diện qua trục là hình vuông \[ABCD\] cạnh \[2\sqrt 3 cm\] với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung của đường tròn đáy sao cho \[\widehat {ABM} = {60^0}.\] Thể tích V của khối tứ diện \[ACDM.\]
A.\[V = 6c{m^3}.\]
B.\[V = 4c{m^3}.\]
C.\[V = 3c{m^3}.\]
D.\[V = 7c{m^3}.\]
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \frac{{m\cos x - 16}}{{\cos x - m}}\] nghịch biến trên khoảng \[\left( {0;\frac{\pi }{3}} \right)\]?
A.7.
B.5.
C.6.
D.8.
Cho hình chóp tứ giác đều \[S.ABCD\] có cạnh đáy bằng \[a\sqrt 2 \] và chiều cao bằng \[\frac{{a\sqrt 2 }}{2}\]. Góc giữa hai mặt phẳng \[\left( {SCD} \right)\] và \[\left( {ABCD} \right)\] bằng
A.\[90^\circ.\]
B.\[45^\circ.\]
C.\[30^\circ.\]
D.\[60^\circ.\]
Trong buổi sinh nhật của thầy Bắc, có 15 đôi yêu nhau tham dự. Mỗi bạn trai bắt tay 1 lần với mọi người trừ bạn gái mình. Các bạn gái không bắt tay với nhau. Hỏi có bao nhiêu cái bắt tay?
A.330.
B.315.
C.420.
D.405.
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] thỏa mãn \[\int\limits_1^9 {\frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} = 4\] và \[\int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)\cos xdx} = 2\]. Tính tích phân \[I = \int\limits_0^3 {f\left( x \right)dx} \].
A.\[I = 2.\]
B.\[I = 6.\]
C.\[I = 10.\]
D.\[I = 4.\]
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - 5y - z = 0\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 3}}{{ - 1}}.\] Viết phương trình đường thẳng Δ vuông góc mặt phẳng (P) tại giao điểm của đường thẳng dvà mặt phẳng (P).
A.\[\Delta:\frac{{x - 2}}{2} = \frac{y}{1} = \frac{{z - 2}}{{ - 1}}.\]
B.\[\Delta:\frac{{x - 2}}{2} = \frac{y}{{ - 5}} = \frac{{z - 2}}{{ - 1}}.\]
C.\[\Delta:\frac{{x - 3}}{3} = \frac{{y - 1}}{1} = \frac{{z - 1}}{1}.\]
D.\[\Delta:\frac{{x - 3}}{2} = \frac{{y - 1}}{{ - 5}} = \frac{{z - 1}}{{ - 1}}.\]
Cho hình chóp \[S.{\mkern 1mu} ABCD\] có đáy \[ABCD\] là hình chữ nhật, \[AB = a,{\mkern 1mu} {\mkern 1mu} BC = 2a.\] Cạnh \[SA = 2a\] và vuông góc với mặt phẳng \[\left( {ABCD} \right).\] Khoảng cách giữa hai đường thẳng BD và SC bằng
A.\[\frac{{a\sqrt 2 }}{3}.\]
B.\[\frac{{a\sqrt 3 }}{2}.\]
C.\[\frac{{3a}}{2}.\]
D.\[\frac{{2a}}{3}.\]
Trong không gian Oxyz,cho mặt cầu \[\left( {{S_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 16\] và \[\left( {{S_2}} \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\] cắt nhau theo giao tuyến là đường tròn (C). Tìm tọa độ tâm của đường tròn (C).
A.\[\left( { - \frac{1}{2};\frac{7}{4};\frac{1}{4}} \right)\]
B.\[\left( {\frac{1}{3};\frac{7}{4};\frac{1}{4}} \right)\]
C.\[\left( { - \frac{1}{3};\frac{7}{4}; - \frac{1}{4}} \right)\]
D.\[\left( { - \frac{1}{2};\frac{7}{4}; - \frac{1}{4}} \right)\]
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ. Bất phương trình \[f\left( x \right) < x + m\] đúng với mọi \[x \in \left( {0;1} \right)\] khi và chỉ khi
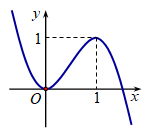
</>
A.\[m \ge f\left( 0 \right).\]
B.\[m \ge f\left( 1 \right) - 1.\]
C.\[m >f\left( 0 \right).\]
D.\[m >f\left( 1 \right) - 1.\]
Cho phương trình \[{x^3} + 2{m^3} = 3{m^2}.\sqrt[3]{{3{m^2}x - 2{m^3}}}\] (m là tham số thực) có tổng các nghiệm thực bằng 10. Mệnh đề nào dưới đây là đúng?
A.\[8 \le m \le 11.\]
B.\[3
C.\[m \le 3.\]
D.\[m \ge 12.\]
Biết rằng \[{2^{x + \frac{1}{x}}} = {\log _2}\left[ {14 - \left( {y - 2} \right)\sqrt {y + 1} } \right]\] trong đó \[x >0.\] Tính giá trị của biểu thức \[P = {x^2} + {y^2} - xy + 1.\]
A.3.
B.1.
C.2.
D.4.
Trong kì thi thử THPT Quốc Gia, Lan làm để thi trắc nghiệm môn Toán. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng; trả lời đúng mỗi câu được 0,2điểm. Lan trả lời hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại Lan chọn ngẫu nhiên. Tính xác suất để điểm thi môn Toán của Lan không dưới 9,5 điểm.
A.\[\frac{9}{{22}}\]
B.\[\frac{{13}}{{1024}}\]
C.\[\frac{2}{{19}}\]
D.\[\frac{{53}}{{512}}\]
Cho hình chóp \[S.ABC\] có cạnh \[BC = 3a\] và \[SA\] vuông góc với mặt phẳng \[\left( {ABC} \right)\]. Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Biết cạnh \[MN = \frac{{9a\sqrt 2 }}{5}\], tính tỉ số \[\frac{{{V_{S.AMN}}}}{{{V_{A.BMNC}}}}.\]
A.\[\frac{{10}}{3}.\]
B.\[\frac{{15}}{7}.\]
C.\[\frac{{16}}{9}.\]
D.\[\frac{{18}}{7}.\]
Cho phương trình \[f\left( x \right) = {x^3} - 3{x^2} - 6x + 1.\] Số nghiệm thực của phương trình \[\sqrt {f\left( {f\left( x \right) + 1} \right) + 1} = f\left( x \right) + 2\] là
A.4.
B.6.
C.7.
D.9.
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số \[y = \left| {f\left( {x - 2020} \right) + m} \right|\] có đúng 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
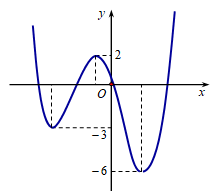
A.12.
B.15.
C.18.
D.9.
Hình phẳng \[\left( H \right)\] được giới hạn bởi đồ thị (C) của hàm số đa thức bậc ba và parabol \[\left( P \right)\] có trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
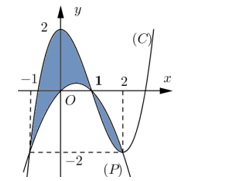
A.\[\frac{{37}}{{12}}.\]
B.\[\frac{7}{{12}}.\]
C.\[\frac{{11}}{{12}}.\]
D.\[\frac{5}{{12}}.\]
Cho phương trình \[{6^x} + m = {\log _6}\left( {x - m} \right)\] (m là tham số thực). Có bao nhiêu giá trị nguyên thuộc khoảng \[\left( { - 6;12} \right)\] của m để phương trình đã cho có nghiệm?
A.6.
B.12.
C.5.
D.10.
Cho hàm số f(x) thỏa mãn \[{\left[ {f'\left( x \right)} \right]^3} + {x^2}.f'\left( x \right) = 2{x^3} + 4{x^2} + 3x + 1,\forall x \in \mathbb{R}\] và \[f\left( 0 \right) = 2.\] Tích phân \[\int\limits_0^6 {f\left( x \right)dx} \] bằng
A.26.
B.66.
C.42.
D.102.
Cho hai số phức \[{z_1}\], \[{z_2}\] thỏa mãn \[\left| {{z_1} + 2 - 3i} \right| = 2\] và \[\left| {\overline {{z_2}} - 1 - 2i} \right| = 1\]. Tìm giá trị lớn nhất của \[\left| {{z_1} - {z_2}} \right|\].
A.\[3 + \sqrt {34} .\]
B.\[3 + \sqrt {10} .\]
C.\[6.\]
D.\[3.\]
Trong không gian Oxyz,cho hai điểm \[M\left( { - 2; - 2;1} \right),\] \[A\left( {1;2; - 3} \right)\] và đường thẳng \[d:\frac{{x + 1}}{2} = \frac{{y - 5}}{2} = \frac{z}{{ - 1}}\]. Tìm một vectơ chỉ phương \[\vec u{\mkern 1mu} {\mkern 1mu} \] của đường thẳng Δ đi qua M, vuông góc với đường thẳng dđồng thời cách điểm A một khoảng bé nhất.
A.\[\vec u = \left( {2;2; - 1} \right)\]
B.\[\vec u = \left( {1;7; - 1} \right)\]
C.\[\vec u = \left( {1;0;2} \right)\]
D.\[\vec u = \left( {3;4; - 4} \right)\]


