35 CÂU HỎI
Khẳng định nào sau đây đúng ?
A.${a^0} = 1$, với mọi số thực a < 0.
B. ${a^0} = 1$, với mọi số thực a > 0.
C.${a^0} = 1$, với mọi số thực a.
D.${a^0} = 1$, với a là số thực khác 0.
Cho 0 <a ¹ 1, 0 <b ¹ 1, x và y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau :
A. \[{\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}\].
B. \[{\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\].
C. \[{\log _a}\left( {x + y} \right) = {\log _a}x + {\log _a}y\].
D. \[{\log _b}x = {\log _b}a.{\log _a}x\].
Trong các hình sau, hình nào là dạng đồ thị của hàm số $y = {a^x},0 < a < 1$?
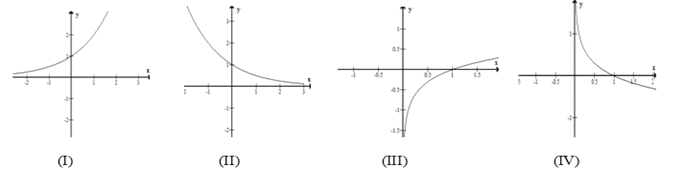
A. (I).
B. (II).
C. (IV).
D. (III).
Trong các hình sau, hình nào là dạng đồ thị của hàm số $y = {\log _a}x,0 < a < 1$
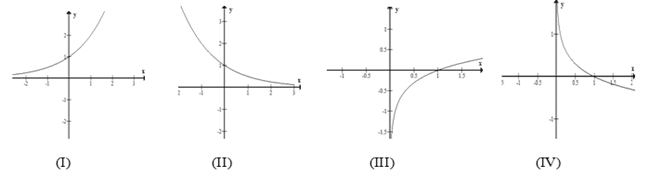
A. (I).
B. (II).
C.(IV).
D. (III).
Giải phương trình ${\log _3}(x - 4) = 0$.
A. $x = 6.$
B. $x = 4.$
C. $x = 1.$
D. $x = 5.$
Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa hai đường thẳng \[m\] và \[n\] bằng góc giữa hai đường thẳng \[a\] và \[b\] cùng đi qua một điểm và tương ứng song song với \[m\] và \[n\].
B. Góc giữa hai đường thẳng \[a\] và \[b\] bất kì luôn là góc tù.
C. Góc giữa hai đường thẳng \[a\] và \[b\] bất kì luôn là góc nhọn.
D. Góc giữa hai đường thẳng \[m\] và \[n\] bằng góc giữa hai đường thẳng \[a\] và \[b\] tương ứng song song với \[m\] và \[n\].
Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
B. Nếu một đường thẳng vuông góc với hai đường thẳng song song thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
C. Nếu đường thẳng a vuông góc với mặt phẳng (P) thì các đường thẳng vuông góc với a cũng vuông góc với (P).
D. Có vô số mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ khi $a$ và $b$ song song (hoặc $a$ trùng với $b$).
C. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $a$ và mặt phẳng $\left( Q \right)$ thì mặt phẳng $\left( P \right)$ song song với mặt phẳng $\left( Q \right)$.
D. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song với $b$.
Cho hình lập phương $ABCD.A'B'C'D'$như hình vẽ
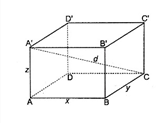
Khẳng định nào sau đây đúng
A.$AA' \bot \left( {ABB'A'} \right)$.
B. $CA' \bot \left( {ABC'D'} \right)$.
C. $AA' \bot \left( {ABCD} \right)$.
D. $CA' \bot \left( {ABCD} \right)$.
Cho hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] cắt nhau và một điểm \[M\] không thuộc \[\left( P \right)\] và \[\left( Q \right)\]. Qua \[M\] có bao nhiêu mặt phẳng vuông góc với \[\left( P \right)\] và \[\left( Q \right)\]?
A. 1.
B. 2.
C. 3.
D. Vô số.
Cho hình chóp $S.ABCD$có đáy $ABCD$ là hình vuông, cạnh bên $SA$ vuông góc với mặt phẳng đáy. Góc phẳng nhị diện $\left[ {S,BC,A} \right]$ là
A. $\widehat {SBA}$.
B. \[\widehat {SCA}\].
C.$\widehat {ASC}$.
D. $\widehat {ASB}$.
Thể tích của khối lăng trụ có diện tích đáy $B$ và chiều cao $h$ là:
A. $\frac{1}{3}Bh$.
B. $Bh$.
C. $\frac{1}{2}Bh$.
D. $3Bh$.
Thể tích của khối chóp có diện tích đáy $B = 6$ và chiều cao$h = 2$bằng:
A. $6$.
B. $3$.
C. $4$.
D. $12$.
Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi A là biến cố : ‘‘Rút được tấm thẻ ghi số chẵn lớn hơn 9’’ ; B là biến cố : ‘‘Rút được tấm thẻ ghi số không nhỏ hơn 8 và không lớn hơn 15’’. Số phần tử của $AB$ là
A. $5$.
B. $6$.
C. $3$.
D. $4$.
Cho $A$, $B$ là hai biến cố xung khắc. Biết $P\left( A \right) = \frac{1}{3}$, $P\left( B \right) = \frac{1}{4}$. Tính $P\left( {A \cup B} \right)$.
A. $\frac{7}{{12}}$.
B. $\frac{1}{{12}}$.
C. $\frac{1}{7}$.
D. $\frac{1}{2}$.
Cho $A$, $B$ là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$.
B. $P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)$.
C. $P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)$.
D. $P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)$.
Cho $A,B$ là hai biến cố độc lập. Biết $P\left( A \right) = 0,5;P\left( {A \cap B} \right) = 0,2$. Tính $P\left( {A \cup B} \right)$.
A. $0,3$.
B. $0,5$.
C. $0,6$.
D. $0,7$.
Một chất điểm chuyển động có phương trình $s\left( t \right) = t + 1$($t$tính bằng giây, $s$tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm $t = 3s$bằng
A. $1{\text{m/s}}.$
B. $15{\text{m/s}}.$
C. $4{\text{m/s}}.$
D. $0{\text{m/s}}{\text{.}}$
Hàm số $y = {x^5}$ có đạo hàm là
A. $y' = 5{x^6}$.
B. $y' = 4{x^5}$.
C. $y' = 5x$.
D. $y' = 5{x^4}$.
Cho $f\left( x \right) = 201$. Tính $f''\left( x \right)$.
A. \[f''\left( x \right) = 2\].
C.\[f''\left( x \right) = 0\].
C.\[f''\left( x \right) = 0\].
D. \[f''\left( x \right) = 1\].
\[{\log _a}\left( {\frac{{{a^2}\sqrt[3]{{{a^2}}}\sqrt[5]{{{a^4}}}}}{{\sqrt[{15}]{{{a^7}}}}}} \right)\] bằng :
A. 3.
B. \[\frac{{12}}{5}\].
C. \[\frac{9}{5}\].
D. 2.
Tập xác định của hàm số ${\text{y}} = {\text{lo}}{{\text{g}}_2}x$ là
A. $\left[ {0; + \infty } \right)$ .
B. $\left( { - \infty ; + \infty } \right)$ .
C.$(0; + \infty )$.
D. $\left[ {2; + \infty } \right)$ .
Số nghiệm của phương trình \[{\log _3}x.{\log _3}\left( {2x - 1} \right) = 2{\log _3}x\] là
A. \[3.\]
B. \[0.\]
C. \[2.\]
D. \[1.\]
Cho hình chóp $S.ABCD$ có $ABCD$ là hình chữ nhật và $SA \bot (ABCD).$ Mệnh đề nào dưới đây đúng ?
A. $AB \bot (SAD).$
B. $BC \bot (SAD).$
C. $AC \bot (SAD).$
D. $BD \bot (SAD).$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a,AD = a\sqrt 2 .$ Cạnh bên $SA \bot (ABCD)$ và$SA = 3a.$ Góc giữa đường thẳng $SC$ và mặt phẳng $(ABCD)$ bằng
A. $45^\circ .$
B. $90^\circ .$
C. $30^\circ .$
D. $60^\circ .$
Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông, $SA$ vuông góc với mặt phẳng đáy. Mặt phẳng $\left( {ABCD} \right)$ vuông góc với mặt phẳng nào dưới đây ?
A. $(SAC).$
B. $(SBD).$
C. $(SCD).$
D. $(SBC).$
Cho hình chóp \[S.ABC\] có \[SA \bot \left( {ABC} \right)\], \[SA = AB = 2a\], tam giác \[ABC\]vuông tại \[B\] (tham khảo hình vẽ). Khoảng cách từ \[A\] đến mặt phẳng \[\left( {SBC} \right)\] bằng
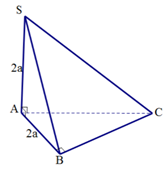
A. $a\sqrt 3 $.
B. $a$.
C. $2a$.
D. $a\sqrt 2 $.
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh $a$. Tính khoảng cách giữa hai đường thẳng $AB'$ và $CD'$.
A.$\frac{{a\sqrt 2 }}{2}.$
B.$a.$
C.$a\sqrt 2 .$
D. $2a.$
Cho khối chóp tứ giác đều \[S.ABCD\]có cạnh đáy bằng \[\sqrt 2 a\]và tam giác \[SAC\]đều. Thể tích của khối chóp đã cho bằng
A.\[\frac{{\sqrt 3 {a^3}}}{2}\].
B.\[\frac{{\sqrt 3 {a^3}}}{3}\].
C.\[\frac{{2\sqrt 3 {a^3}}}{3}\].
D.\[\frac{{3\sqrt 3 {a^3}}}{2}\].
Một hộp chứa $5$ viên bi đỏ và $4$ viên bi xanh. Lấy ngẫu nhiên đồng thời 2 viên bi, xác suất để lấy được ít nhất một viên bi màu xanh bằng
A. $\frac{5}{9}.$
B. $\frac{5}{{18}}.$
C. $\frac{{13}}{{18}}.$
D. $\frac{5}{6}.$
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn không trúng bằng
A.\[\frac{1}{{12}}\].
B.\[\frac{{11}}{{12}}\].
D.\[\frac{3}{{25}}\].
D.\[\frac{3}{{25}}\].
Trong đợt thi tốt nghiệp THPT năm 2023 của các trường THPT, thống kê cho thấy \[95\% \] học sinh tỉnh \[X\] đậu tốt nghiệp THPT, \[97\% \] học sinh tỉnh \[Y\] đậu tốt nghiệp THPT. Chọn ngẫu nhiên một học sinh tỉnh \[X\] và một học sinh tỉnh \[Y\]. Giả thiết chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để chỉ có đúng một học sinh được chọn đậu tốt nghiệp THPT.
A.\[0,177\].
B. \[0,077\].
C.\[0,999\].
D.\[0,899\].
Cho hàm số $y = - {x^3} + 3x - 2$ có đồ thị $\left( C \right).$Phương trình tiếp tuyến của $\left( C \right)$ tại giao điểm của $\left( C \right)$ với trục tung là
A. $y = - 2x + 1$.
B. $y = 2x + 1$.
C. $y = 3x - 2$.
D. $y = - 3x - 2$.
Hàm số \[y = \frac{{{x^2} + x}}{{x - 1}}\]có đạo hàm $y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}$. Khi đó \[S = a + b + c\] có kết quả là
A.$S = 1$.
B.$S = - 2$.
C.$S = 0$.
D.$S = - 3$.
Cho hàm số$f\left( x \right) = {\left( {x + 1} \right)^3}$. Giá trị$f''\left( 0 \right)$bằng
A.6.
B.3.
C.12.
D.24.

