35 CÂU HỎI
Nguyên hàm của hàm số là :
A.
B.
C.
D.
Tìm là:
A.
B.
C.
D.
F(x) là nguyên hàm của hàm số . F(x) là hàm số nào sau đây?
A.
B.
C.
D.
Để tính theo phương pháp tính nguyên hàm từng phần, ta đặt:
A.
B.
C.
D.
Kết quả của là:
A.
B.
C.
D.
Giả sử và và thì bằng bao nhiêu?
A. 5
B. 1
C. -1
D. -5
Cho hàm số f liên tục trên R và số thực dương a. Trong các đẳng thức sau, đẳng thức nào luôn đúng?
A.
B.
C.
D.
Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [0;2]. Biết rằng và . Tích phân có giá trị bằng
A. 3
B. 0
C. -2
D. -4
Tính
A.
B.
C.
D.
Tích phân bằng
A.
B.
C.
D.
Tích phân bằng
A.
B.
C.
D.
Biết rằng . Giá trị của a là :
A. 9
B. 3
C. 27
D. 81
Tích phân bằng:
A. -1
B. 1
C. 2
D. 0
Cho , ta tính được:
A. I = cos1
B. I = 1
C. I = sin1
D. Một kết quả khác
Tích phân bằng :
A.
B.
C.
D.
Tích phân bằng:
A.
B.
C.
D.
Tính tích phân .
A. 4
B. 3
C. 5
D. 6
Cho hàm số f liên tục trên R thỏa , với mọi xR. Giá trị của tích phân là
A. 2
B. -7
C. 7
D. -2
Diện tích hình phẳng giới hạn bởi các đường ; và là
A.
B.
C.
D.
Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường , trục Ox , x=-1, x=1 một vòng quanh trục Ox là:
A.
B.
C.
D.
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;1] thỏa mãn và . Tích phân
A.
B.
C.
D.
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [1;4], đồng biến trên đoạn [1;4] và thỏa mãn đẳng thức . Biết rằng , tính
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ , cho . Khi đó: có tọa độ bằng
A.
B.
C.
D.
Trong không gian Oxyz, điểm M nằm trên mặt phẳng , cách đều ba điểm có tọa độ là:
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3), trên trục Oz lấy điểm M sao cho . Tọa độ của điểm M là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz cho véctơ . Giá trị của m để đồng phẳng là:
A.
B.
C.
D. 1
Trong không gian với hệ trục tọa độ Oxyz cho . Khi đó tọa độ trọng tâm G của tam giác ABC là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho A(2; 0; 0), B(0; 3; 1), C(-3; 6; 4). Gọi M là điểm nằm trên đoạn BC sao cho MC = 2MB. Độ dài đoạn AM là:
A.
B.
C.
D.
Trong không gian Oxyz, cho tam giác ABC có tọa độ các đỉnh và C( -m- 2; 1- m; m + 5). Tìm m để tam giác ABC vuông tại B.
A. m = 3
B. m = -3
C. m = 4
D. m = -4
Trong không gian với hệ tọa độ Oxyz , cho ba vectơ . Khi đó để ba vectơ 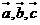 đồng phẳng thì giá trị của tham số thực m bằng bao nhiêu?
đồng phẳng thì giá trị của tham số thực m bằng bao nhiêu?
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz , cho vectơ ![]() ,
, ![]() cùng phương với vectơ . Biết vectơ tạo với tia Oy một góc nhọn và
cùng phương với vectơ . Biết vectơ tạo với tia Oy một góc nhọn và ![]() . Khi đó tổng
. Khi đó tổng ![]() bằng bao nhiêu?
bằng bao nhiêu?
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz , cho A(1;-1;0) , B(2;1;1) , C(-1;0;-1) , D(m;m-3;1). Tìm tất cả các giá trị thực của m để ABCD là một tứ diện .
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz , cặp mặt phẳng nào sau đây cắt nhau ?
A. 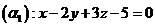 và
và 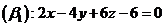
B. ![]() và
và ![]()
C. 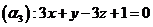 và
và ![]()
D. ![]() và
và ![]()
Trong không gian Oxyz, cho điểm . M là điểm thay đổi trong không gian thỏa mãn . Khi đó độ dài OM lớn nhất bằng?
A.
B.
C.
D.
Cho tam giác ABC với . Độ dài phân giác trong của kẻ từ đỉnh B là
A.
B.
C.
D.


