50 CÂU HỎI
Trong không gian tọa độ Oxyz, cho . Tọa độ của vectơ bằng
A. (-3; 2; 1).
B. (2; -3; 0).
C. (2; -3; 1).
D. (-3; 2; 0).
Hàm số y = x3 - 3x - 2022 nghịch biến trên khoảng
A. (-1; 1)
B. (0; 3)
C. (-; -1)
D. (1; 3)
Cho một hình nón có bán kính mặt đáy bằng r và độ dài đường sinh bằng l. Diện tích xung quanh của hình nón bằng
A.
B.
C.
D.
Cho biết và . Giá trị của tích phân bằng
A. 3
B. 9
C. 2
D. 18
Khối lập phương là khối đa diện đều loại
A. {4;3}
B. {3;4}
C. {3;3}
D. {5;3}
Hàm số đạt cực đại tại điểm
A. x = 0
B. x = 3
C. x = 2
D. x = 1
Tập xác định của hàm số là
A.
B.
C.
D.
Cho a là một số thực dương. Giá trị của biểu thức bằng
A. 4
B. 2
C. 8
D. 1
Trong không gian tọa độ Oxyz, phương trình mặt cầu tâm O(0; 0; 0), bán kính bằng 2 là
A. x2 + y2 + z2 = 2
B. x2 + y2 = 4
C. x + y + z = 2
D. x2 + y2 + z2 = 4
Đạo hàm của hàm số y = 2x là
A.
B.
C.
D.
Trong không gian tọa độ Oxyz, cho . Giá trị của tích vô hướng bằng
A. 3.
B. -3.
C. 2.
D. -2.
Phương trình đường tiệm cận ngang của đồ thị hàm số là
A. y = -1
B. y = 2
C. y = 1
D. y = -2
Trong không gian tọa độ Oxyz, phương trình mặt phẳng đi qua điểm M(-1; 2; 1) và nhận vectơ làm vectơ pháp tuyến là
A. 2x - y - z + 5 = 0
B. 2x - y - z - 5 = 0
C. - x + 2y - z + 5 = 0
D. - x + 2y - z - 5 = 0
Cho biết và . Giá trị của tích phân bằng
A. 5
B. 2
C. 3
D. 1
Tập xác định của hàm số là
A.
B.
C.
D.
Họ các nguyên hàm là
A.
B.
C.
D.
Trong mặt phẳng tọa độ Oxy, gọi (C) là đồ thị của hàm số . Phương trình tiếp tuyến của (C) tại giao điểm của đồ thị (C) với trục hoành là
A. y = x - 1
B. y = - x + 1
C. y = x - 2
D. y = - x + 2
Cho log2 3 = a. Giá trị của biểu thức P = log6 12 tính theo a bằng
A.
B.
C.
D.
Trên mặt phẳng tọa độ Oxy, cho hàm số y = f (x) liên tục trên [a; b] và có đồ thị là (C). Thể tích khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi (C), trục hoành, đường thẳng x = a và x = b bằng
A. .
B. .
C. .
D. .
Đồ thị trong hình vẽ dưới đây là của hàm số nào?
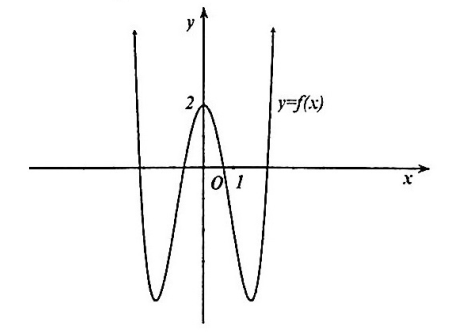
A. y = – x4 + 3x2 + 2
B. y = x4 + 2
C. y = x4 – 5x2 + 2
D. y = – x4 + 2
Cho khối nón có góc ở đỉnh bằng 90°, độ dài đường sinh bằng a. Thể tích khối nón bằng
A. .
B. .
C. .
D. .
Gọi x1, x2 là 2 nghiệm của phương trình 6x + 12 = 3x+1 + 2x+2. Tích x1.x2 bằng
A. 4
B. 1
C. 3
D. 2
Họ các nguyên hàm là
A. x.2x + C
B. 2x + C
C. 2x ln 2 + C
D.
Họ các nguyên hàm là
A. ln (2x + 1) + C
B.
C.
D.
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin3 x + 9cos2 x + 6sin x -10. Giá trị của tích M.m bằng
A. 5
B.
C. 0.
D.
Gọi F (x) là một nguyên hàm của hàm số f (x) = ex thỏa mãn F (0) = 2. Giá trị của F (1) bằng
A. e - 2
B. e + 2
C. 2
D. e + 1
Họ các nguyên hàm là
A.
B.
C.
D.
Tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (-; -2) là
A. .
B. .
C. .
D. .
Họ các nguyên hàm là
A.
B.
C.
D.
Cho F (x) là một nguyên hàm của hàm số f (x) = x.(x2 + 1)2022 thỏa mãn . Giá trị của F (1) bằng
A. 22023
B.
C. 22022
D. .
Gọi a, b là các số nguyên dương nhỏ nhất sao cho . Giá trị của a + b.
A. 5
B. 7
C. 6
D. 12
Trong không gian tọa độ Oxyz, cho 2 điểm A(-1; 2; 0), B(3; 2; 2). Phương trình mặt phẳng trung trực của đoạn AB là
A. 2x + z - 3 = 0
B. 2x - z + 3 = 0
C. 2x + y - 3 = 0
D. 2x - y - 3 = 0
Gọi a, b là các số nguyên sao cho . Giá trị của a2 + b2 bằng
A. 3
B. 8
C. 4
D. 5
Gọi a, b là các số hữu tỉ sao cho . Giá trị của tích ab bằng
A.
B.
C.
D.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x3, trục hoành và đường thẳng x = 1 bằng
A.
B. .
C. 1.
D.
Một xe ô tô đang đi với vận tốc 10 m/s thì người lái xe bắt đầu đạp phanh, từ thời điểm đó xe chuyển động chậm dần đều với vận tốc v (t) = 10 - 5t (m/s), ở đó t tính bằng giây. Quãng đường ô tô dịch chuyển từ lúc đạp phanh đến lúc dừng hẳn bằng
A. 5 m
B. 10 m
C. 15 m
D. 12 m
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD và điểm O tùy ý trên mặt phẳng (BCD). Thể tích tứ diện OMNP bằng
A. .
B. .
C. .
D. .
Cho hai số tự nhiên x, y thỏa mãn x.log28 2 + y.log28 7 = 2. Giá trị x + y bằng
A. 5
B. 6
C. 4
D. 8
Cho hình chóp S.ABC có SA (ABC), và . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng
A.
B.
C.
D.
Cho hình chóp S.ABC có SA (ABC), SA = AB = BC = a và . Khoảng cách từ A đến mặt phẳng (SBC) bằng
A.
B.
C.
D.
Cho hình chóp S.ABC có SAC, ABC là những tam giác đều cạnh bằng a và (SAC) (ABC). Gọi là góc giữa hai mặt phẳng (SBC) và (ABC). Giá trị của tan bằng
A. .
B. 3.
C. .
D. 2.
Trong không gian tọa độ Oxyz, cho A(-1; 2; 2), B(2; -1; -2). Diện tích tam giác OAB bằng
A. .
B. .
C. .
D. .
Trong không gian tọa độ Oxyz, cho hai điểm A(-1; 2; 0), B(-3; 4; 2). Phương trình mặt cầu đường kính AB là
A. (x + 2)2 + (y - 3)2 + (z - 1)2 = 3
B. (x + 2)2 + (y - 3)2 + (z - 1)2 = 9
C. (x - 2)2 + (y + 3)2 + (z + 1)2 = 3
D. (x - 2)2 + (y + 3)2 + (z + 1)2 = 9
Trong không gian tọa độ Oxyz, gọi (P) là mặt phẳng đi qua 2 điểm A(0; 1; -2), B(2; 1; 0) sao cho khoảng cách từ gốc tọa độ O đến (P) lớn nhất. Phương trình của mặt phẳng (P) là
A. x - y - z + 3 = 0
B. x + y - z - 3 = 0
C. x - 2y - z - 3 = 0
D. 2x - y - z - 3 = 0
Cho hàm số f (x) liên tục và có đạo hàm trên [0; 1]. Biết và f (0) = f (1) = 7. Giá trị của tích phân bằng
A. 7
B. 5
C. 2
D. 1
Trong không gian Oxyz, cho hai điểm A(-1; 0; 2), B(3; 2; -2). Biết tập hợp các điểm M thỏa mãn MA2 + MB2 = 30 là một mặt cầu. Bán kính mặt cầu đó bằng
A.
B. 6.
C. 2.
D.
Cho phương trình với tham số m. Số giá trị nguyên dương của m để phương trình đã cho có nghiệm là
A. 4.
B. 2.
C. 3.
D. 1.
Cho biết hàm số có giá trị lớn nhất bằng 3 khi x [0; 3]. Số các giá trị của tham số m thỏa mãn là
A. 2.
B. 3.
C. 1.
D. 4.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có , AD = a và . Gọi M là trung điểm của cạnh AB. Thể tích tứ diện A’C’DM bằng
A.
B.
C.
D.
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
A.
B.
C.
D.


