Quiz

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 6)

Admin40 câu hỏiToánLớp 12

40 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

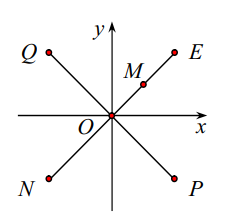
Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z. Điểm nào trong hình vẽ là điểm biểu diễn của số phức 2z? Media VietJack

A. Điểm Q

B. Điểm P

C. Điểm E

D. Điểm N

2. Nhiều lựa chọn

Tìm x + y thỏa mãn (2x – 3yi) + (1 – 3i) = –1 + 6i với i là đơn vị ảo.

A. –4

B. 4

C. 5

D. –2

3. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M(1; 3; –2), cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho $\frac{O A}{1} = \frac{O B}{2} = \frac{O C}{4}$ .

A. x + 2y + 4z + 1 = 0

B. 2x – y – z – 1 = 0

C. 4x + 2y + z – 8 = 0

D. x + 2y + 4z + 10 = 0

4. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 1; 1) và B(1; 2; 3). Viết phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB.

A. x + 3y + 4z – 26 = 0

B. x + y + 2z – 6 = 0

C. x + 3y + 4z – 7 = 0

D. x + y + 2z – 3 = 0

5. Nhiều lựa chọn

Trong không gian Oxyz, hình chiếu vuông góc của điểm A(1; 2; 5) trên trục Ox có tọa độ là

A. (1; 0; 0)

B. (0; 2; 5)

C. (0; 0; 5)

D. (0; 2; 0)

6. Nhiều lựa chọn

Cho hàm số y = f (x) liên tục trên ℝ. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f (x), y = 0, x = –1 và x = 5 (như hình vẽ bên).

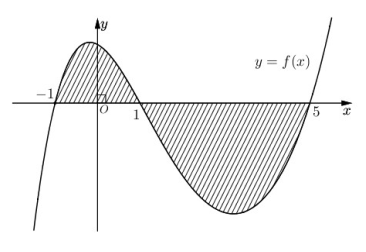
Media VietJack

Mệnh đề nào sau đây đúng?

A. $- \int_{- 1}^{1} f (x) d x - \int_{1}^{5} f (x) d x$ .

B. $\int_{- 1}^{1} f (x) d x + \int_{1}^{5} f (x) d x$ .

C. $\int_{- 1}^{1} f (x) d x - \int_{1}^{5} f (x) d x$ .

D. $- \int_{- 1}^{1} f (x) d x + \int_{1}^{5} f (x) d x$ .

7. Nhiều lựa chọn

Trong không gian Oxyz, cho 3 điểm A(1; 0; 0), B(0; –2; 3), C(1; 1; 1). Gọi (P) là mặt phẳng chứa A, B sao cho khoảng cách từ C tới mặt phẳng (P) bằng $\frac{2}{\sqrt{3}}$ . Phương trình mặt phẳng (P) là:

A. 2x + 3y + z – 1 = 0 hoặc 3x + y + 7z + 6 = 0

B. x + y + z – 1 = 0 hoặc –2x + 37y + 17z + 13 = 0

C. x + y + 2z – 1 = 0 hoặc –2x + 3y + 7z + 23 = 0

D. x + y + z – 1 = 0 hoặc –23x + 37y + 17z + 23 = 0

8. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình 3x + 4y + 2z + 4 = 0 và điểm A(1; –2; 3). Tính khoảng cách d từ A đến (P).

A. $d = \frac{5}{29}$ .

B. $d = \frac{5}{9}$ .

C. $d = \frac{\sqrt{5}}{3}$ .

D. $d = \frac{5}{\sqrt{29}} .$

9. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; –2; 7), B (–3; 8; –1). Mặt cầu đường kính AB có phương trình là

A. ${(x - 1)}^{2} + {(y - 3)}^{2} + {(z + 3)}^{2} = \sqrt{45}$

B. (x + 1)² + (y – 3)² + (z – 3)² = 45

C. (x – 1)² + (y + 3)² + (z + 3)² = 45

D. ${(x + 1)}^{2} + {(y - 3)}^{2} + {(z - 3)}^{2} = \sqrt{45}$ .

10. Nhiều lựa chọn

Biết z là số phức có phần ảo âm và là nghiệm của phương trình z² – 6z + 10 = 0. Tính tổng phần thực và ảo của số phức $w = \frac{z}{\bar{z}}$ .

A. $\frac{7}{5}$ .

B. $\frac{1}{5}$ .

C. $\frac{2}{5} .$

D. $\frac{4}{5}$ .

11. Nhiều lựa chọn

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0; 0; –3) và đi qua điểm M(4; 0; 0). Phương trình của (S) là

A. x² + y² + (z + 3)² = 5

B. x² + y² + (z + 3)² = 25

C. x² + y² + (z – 3)² = 25

D. x² + y² + (z – 3)² = 5

12. Nhiều lựa chọn

Cho hàm số f (x) thỏa mãn $f^{'} (x) = 3 - 4 e^{2 x}$ và f (0) = 10. Mệnh đề nào dưới đây đúng?

A. f (x) = 3x – 4e^2x + 10

B. f (x) = 3x – 4e^2x + 14

C. f (x) = 3x – 2e^2x + 12

D. f (x) = 3x – 2e^2x + 10

13. Nhiều lựa chọn

Trong không gian Oxyz, cho vectơ $\vec{a} = (2; - 2; - 4), \vec{b} = (1; - 1; 1)$ . Mệnh đề nào dưới đây sai?

A. $\cos (\vec{a}; \vec{b}) = 0$

B. $\vec{a}$ và $\vec{b}$ cùng phương

C. $| \vec{b} | = \sqrt{3}$ .

D. $\vec{a} ⊥ \vec{b}$ .

14. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm M (1;2;–3) và có một vectơ pháp tuyến $\vec{n} = (1; - 2; 3)$

A. x – 2y – 3z – 6 = 0

B. x – 2y – 3z + 6 = 0

C. x – 2y + 3z + 12 = 0

D. x – 2y + 3z – 12 = 0

15. Nhiều lựa chọn

Cho số phức $z = \frac{(2 - 3 i) (4 - i)}{3 + 2 i}$ . Tìm tọa độ điểm biểu diễn số phức $\bar{z}$ trên mặt phẳng Oxy.

A. (1; 4)

B. (–1; 4)

C. (1; –4)

D. (–1; –4)

16. Nhiều lựa chọn

Cho số phức z thỏa mãn $3 (\bar{z} + i) - (2 - i) z = 3 + 10 i$ . Môđun của z bằng

A. $\sqrt{5}$ .

B. $\sqrt{3}$ .

C. 3.

D. 5.

17. Nhiều lựa chọn

Cho tích phân $I = \int_{0}^{1} \frac{x^{7}}{{(1 + x^{2})}^{5}} dx$ , giả sử đặt t = 1 + x². Tìm mệnh đề đúng.

A. $I = \frac{3}{2} \int_{1}^{4} \frac{{(t - 1)}^{3}}{t^{4}} d t$

B. $I = \int_{1}^{3} \frac{{(t - 1)}^{3}}{t^{5}} d t$

C. $I = \frac{1}{2} \int_{0}^{1} \frac{{(t - 1)}^{3}}{t^{5}} d t$

D. $I = \frac{1}{2} \int_{1}^{2} \frac{{(t - 1)}^{3}}{t^{5}} d t$

18. Nhiều lựa chọn

Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:

A. $V = π \int_{a}^{b} f^{2} (x) dx$

B. $V = π^{2} \int_{a}^{b} f^{2} (x) dx$

C. $V = 2 π \int_{a}^{b} f^{2} (x) dx$

D. $V = π^{2} \int_{a}^{b} f (x) dx$

19. Nhiều lựa chọn

Cho hai số phức z = 1 + 3i và w = 1 + i. Mô đun của số phức $z . \bar{w}$ bằng

A. $2 \sqrt{2}$ .

B. $2 \sqrt{5}$ .

C. 20.

D. 8.

20. Nhiều lựa chọn

Cho $\int_{- 2}^{2} f (x) d x = 1, \int_{- 2}^{4} f (t) d t = - 4$ . Tính $\int_{2}^{4} f (y) d y$ .

A. I = 5

B. I = –3

C. I = 3

D. I = –5

21. Nhiều lựa chọn

Tính diện tích hình phẳng giới hạn đồ thị hàm số y = x³ – x và đồ thị hàm số y = x – x².

A. $\frac{37}{12}$ .

B. $\frac{9}{4}$ .

C. $\frac{81}{12}$ .

D. 13

22. Nhiều lựa chọn

Tính thể tích của vật thể tạo nên khi quay quanh trục Ox hình phẳng D giới hạn bởi đồ thị (P) : y = 2x – x² và trục Ox bằng:

A. $\frac{17 π}{15}$ .

B. $\frac{16 π}{15}$ .

C. $\frac{19 π}{15}$ .

D. $\frac{13 π}{15}$ .

23. Nhiều lựa chọn

Cho số phức z = m + 3i. Tìm m để số phức $w = i \bar{z} + 3 z$ là số thuần ảo?

A. m = 1

B. $m = \frac{- 9}{4}$

C. $m = - 1$

D. m = –3

24. Nhiều lựa chọn

Hàm số F (x) là một nguyên hàm của hàm số f(x) trên khoảng K nếu

A. $f^{'} (x) = F (x), \forall x \in K$

B. $F^{'} (x) = f (x), \forall x \in K$

C. $F^{'} (x) = - f (x), \forall x \in K$

D. $f^{'} (x) = - F (x), \forall x \in K$

25. Nhiều lựa chọn

Trong mặt phẳng tọa độ Oxy, 3 điểm A, B, C lần lượt là điểm biểu diễn của ba số phức z₁ = 3 – 7i, z₂ = 9 – 5i và z₃ = –5 + 9i. Khi đó, trọng tâm G của tam giác ABC là điểm biểu diễn của số phức nào sau đây?

A. $z = \frac{7}{3} - i$ .

B. z = 1 – 9i

C. z = 2 + 2i

D. z = 3 + 3i

26. Nhiều lựa chọn

Trong không gian Oxyz, cho hai điểm A(3; 1; –2), B (2; –3; 5). Điểm M thuộc đoạn AB sao cho MA = 2MB, tọa độ điểm M là

A. (4; 5; –9)

B. $(\frac{7}{3}; \frac{5}{3}; \frac{17}{2})$

C. $(\frac{7}{3}; - \frac{5}{3}; \frac{8}{3})$

D. (1; –7; 12)

27. Nhiều lựa chọn

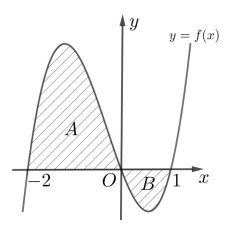
Cho hàm số y = f (x) có đồ thị như hình vẽ và diện tích hai phần A, B lần lượt bằng 11 và 2. Giá trị của $I = \int_{- 1}^{0} f (3 x + 1) d x$ bằng Media VietJack

A. 9

B. 13

C. $\frac{13}{3}$

D. 3

28. Nhiều lựa chọn

Xét các số phức z thỏa mãn $(\bar{z} + 2 i) (z - 2)$ là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng

A. $\sqrt{2}$ .

B. 4.

C. 2.

D. $2 \sqrt{2}$ .

29. Nhiều lựa chọn

Trong không gian Oxyz, cho (P) : x + y – 2z + 5 = 0 và (Q) : 4x + (2 – m)y + mz – 3 = 0, m là tham số thực. Tìm tham số m sao cho mặt phẳng (Q) vuông góc với mặt phẳng (P).

A. m = –3

B. m = –2

C. m = 3

D. m = 2

30. Nhiều lựa chọn

Cho $\int_{5}^{21} \frac{d x}{x \sqrt{x + 4}} = a \ln 3 + b \ln 5 + c \ln 7$ , với a, b, c là các số hữu tỉ. Mệnh đề nào sau đây đúng?

A. a – b = –2c

B. a + b = –2c

C. a + b = c

D. a – b = –c

31. Nhiều lựa chọn

Khẳng định nào trong các khẳng định sau đúng với mọi hàm f, g liên tục trên K và a, b là các số bất kỳ thuộc K?

A. $\int_{a}^{b} [f (x) . g (x)] d x = \int_{a}^{b} f (x) d x . \int_{a}^{b} g (x) d x$

B. $\int_{a}^{b} [f (x) + 2 g (x)] d x = \int_{a}^{b} f (x) d x + 2 \int_{a}^{b} g (x) d x$

C. $\int_{a}^{b} \frac{f (x)}{g (x)} d x = \frac{\int_{a}^{b} f (x) d x}{\int_{a}^{b} g (x) d x}$

$\int_{a}^{b} f^{2} (x) d x = {[\int_{a}^{b} f (x) d x]}^{2}$

32. Nhiều lựa chọn

Cho số phức z thỏa mãn (3 + 2i)z + (2 – i)² = 4 + i. Tìm tọa độ điểm M biểu diễn số phức z.

A. M(–1; 1)

B. M (–1; –1)

C. M(1; 1)

D. M(1; –1)

33. Nhiều lựa chọn

Số phức có phần thực bằng 1 và phần ảo bằng 3 là

A. 1 + 3i

B. –1 + 3i

C. –1 – 3i

D. 1 – 3i

34. Nhiều lựa chọn

Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0; 1] thỏa mãn $\int_{0}^{1} {[f^{'} (x)]}^{2} d x = \int_{0}^{1} (x + 1) e^{x} f (x) d x = \frac{e^{2} - 1}{4}$ và f (1) = 0. Tính $\int_{0}^{1} f (x) d x$ .

A. $\frac{e - 1}{2}$ .

B. $\frac{e^{2}}{4} .$

C. e – 2

D. $\frac{e}{2}$ .

35. Nhiều lựa chọn

Tìm nguyên hàm của hàm số $f (x) = \frac{x^{4} + 2}{x^{2}}$

A. $\int f (x) dx = \frac{x^{3}}{3} + \frac{2}{x} + C$ .

B. $\int f (x) dx = \frac{x^{3}}{3} - \frac{1}{x} + C$ .

C. $\int f (x) dx = \frac{x^{3}}{3} - \frac{2}{x} + C$ .

D. $\int f (x) dx = \frac{x^{3}}{3} + \frac{1}{x} + C$ .

36. Nhiều lựa chọn

Giả sử $I = \int_{0}^{\frac{π}{4}} \sin 3 x d x = a + b \frac{\sqrt{2}}{2} (a, b \in ℚ)$ . Khi đó giá trị a – b là

A. 0

B. $- \frac{3}{10}$ .

C. $- \frac{1}{6}$ .

D. $\frac{1}{5}$ .

37. Nhiều lựa chọn

Trong không gian Oxyz, cho mặt phẳng (P) : 2y – 3z + 1 = 0. Chọn đáp án sai?

A. VTPT : $\vec{n} = (0; 2; - 3)$ .

B. M(1; 1; 1) $\in$ (P)

C. (P) // Ox

D. Ox $\subset$ (P)

38. Nhiều lựa chọn

Xét tất cả các số phức z thỏa mãn $| z - 3 i + 4 | = 1$ . Giá trị nhỏ nhất của $| z^{2} + 7 - 24 i |$ nằm trong khoảng nào?

A. (0; 1009)

B. (2018; 4036)

C. (4036; +∞)

D. (1009; 2018)

39. Nhiều lựa chọn

Mô đun của số phức liên hợp của số phức z = –2 + 5i là

A. 29

B. $\sqrt{9}$ .

C. $\sqrt{7}$ .

D. $\sqrt{29}$ .

40. Nhiều lựa chọn

Trong không gian với hệ trục tọa độ Oxyz, tìm tọa độ tâm I và bán kính R của mặt cầu (x – 1)² + (y + 2)² + (z – 4)² = 20.

A. $I (- 1; 2; - 4), R = 2 \sqrt{5}$

B. I (1;–2;4), R = 20

C. $I (1; - 2; 4), R = 2 \sqrt{5}$

D. $I (- 1; 2; - 4), R = 5 \sqrt{2}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube