35 CÂU HỎI
Cho góc lượng giác $\left( {Oa,Ob} \right)$ có số đo là $50^\circ .$ Hỏi số đo của góc luọng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là $Oa$ và tia cuối là $Ob?$
A. ${\alpha _1} = 140^\circ .$
B. ${\alpha _2} = 410^\circ .$
C. ${\alpha _3} = 320^\circ .$
D. ${\alpha _4} = 230^\circ .$
Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác như hình vẽ bên dưới. Điểm nào trong bốn đáp án A, B, C, D biểu diễn cho góc lượng giác có số đo bằng $60^\circ ?$
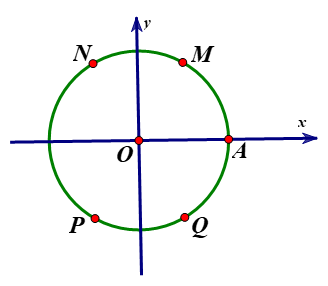
A. Điểm $N.$
B. Điểm $M.$
C. Điểm $P.$
D. Điểm $Q.$
Đổi số đo của góc $\alpha = - 45^\circ $ sang rađian.
A. $\alpha = - \frac{\pi }{2}.$
B. $\alpha = \frac{\pi }{2}.$
C. $\alpha = - \frac{\pi }{4}.$
D. $\alpha = \frac{\pi }{4}.$
Cho $\alpha $ thuộc góc phần phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
A. $\sin \alpha > 0$.
B. $\cos \alpha < 0$.
C. $\tan \alpha > 0$.
D.$\cot \alpha > 0$.
Điểm cuối của góc lượng giác $\alpha $ở góc phần tư phần thứ mấy nếu $\sqrt {{{\sin }^2}\alpha } = \sin \alpha $.
A.Thứ III.
B.Thứ I hoặc III.
C.Thứ I hoặc II.
D. Thứ III hoặc IV.
Cho góc $\alpha $ thỏa mãn $\cot \alpha = \frac{3}{4}$ và $0^\circ < \alpha < 90^\circ $. Khẳng định nào sau đây đúng?
A. $\cos \alpha = - \frac{4}{5}$.
B. $\cos \alpha = \frac{4}{5}$.
C. $\sin \alpha = \frac{4}{5}$.
D. $\sin \alpha = - \frac{4}{5}$.
Công thức nào sau đây đúng?
A. $\cos \alpha = - \frac{4}{5}$.
B. $\tan \left( {a + b} \right) = \tan \,a + \tan \,b$.
C. $\sin \left( {a - b} \right) = \sin a\cos b + \cos a\sin b$.
D. $cos\left( {a + b} \right) = \cos a\,\cos b - \sin a\sin b.$
Cho $\cos x + \sin x \ne 0$. Rút gọn biểu thức $P = \frac{{2{{\cos }^2}x - 1}}{{\cos x + \sin x}}$ ta được
A. \[P = \cos x - \sin x\].
B. \[P = - \cos x - \sin x\].
C. \[P = \sin x - \cos x\].
D. \[\cos x + \sin x\]
Nếu $\operatorname{s} {\text{inx}} + \cos x = \frac{1}{2}$ thì $\sin 2x$ bằng
A. $\frac{3}{4}$.
B. $\frac{3}{8}$.
C. $\frac{{\sqrt 2 }}{2}$.
D. $\frac{{ - 3}}{4}$.
Trong các hàm số sau đây, hàm số nào sau đây là hàm số chẵn?
A. $y = \frac{{\sin x}}{{{x^2}}}.$
B. $y = {x^2}\tan x.$
C. $y = \frac{{{x^2}}}{{\cos x}}.$
D. $y = x + \sin x.$
Tìm tập giá trị $T$ của hàm số \[y = 5 - 3\sin x.\]
A. $T = \left[ { - 1;1} \right].$
B. $T = \left[ { - 3;3} \right].$
C. $T = \left[ {2;8} \right].$
D. $T = \left[ {5;8} \right].$
Tìm giá trị lớn nhất $M$ và giá trị nhỏ nhất $m$ của hàm số $y = \sqrt {7 - 3{{\cos }^2}x} .$
A. $M = \sqrt {10} ,{\text{ }}m = 2.$
B. $M = \sqrt 7 ,{\text{ }}m = 2.$
C. $M = \sqrt {10} ,{\text{ }}m = \sqrt 7 .$
D. $M = 0,{\text{ }}m = 1.$
Nghiệm của phương trình $\sin x = 1$ là
A.$x = - \frac{\pi }{2} + k2\pi $.
B.$x = \frac{\pi }{2} + k\pi $.
C.$x = k\pi $.
D. $x = \frac{\pi }{2} + k2\pi $.
Tất cả nghiệm của phương trình $\cot 2x = \cot \frac{\pi }{3}$ là
A. $x = \frac{\pi }{6} + k\pi ,\,\,k \in \mathbb{Z}$.
B. $x = \frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}$.
C. $x = \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}$.
D. $x = \frac{\pi }{6} + k\frac{\pi }{2},\,\,k \in \mathbb{Z}$.
Tất cả nghiệm của phương trình $\sin x = \frac{1}{2}$ là
A. $x = \frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}$.
B. $x = \frac{{5\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}$.
C. $x = \frac{\pi }{6} + k2\pi $ và $x = - \frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}$.
D. $x = \frac{\pi }{6} + k2\pi $ và $x = \frac{{5\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}$.
Tất cả nghiệm của phương trình $\cot \left( {\frac{x}{2} + \frac{\pi }{4}} \right) = - 1$ là
A. $x = - \frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}$.
B. $x = - \pi + k\pi ,\,\,k \in \mathbb{Z}$.
C. $x = - \frac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}$.
D. $x = - \pi + k2\pi ,\,\,k \in \mathbb{Z}$.
Cho các dãy số sau. Dãy số nào là dãy số tăng?
A. \[1;\,\,1;\,\,1;\,\,1;1;...\].
B. \[1;\,\, - \frac{1}{2};\,\,\frac{1}{4}; - \frac{1}{8};\frac{1}{{16}};...\].
C. \[1;\,3;\,\,5;\,\,7;\,\,9;...\].
D. \[1;\,\,\frac{1}{2};\,\,\frac{1}{4};\,\,\frac{1}{8};\,\,\frac{1}{{16}};...\].
Trong các dãy số $\left( {{u_n}} \right)$ cho bởi số hạng tổng quát ${u_n}$ sau, dãy số nào là dãy số giảm?
A. \[{u_n} = \frac{1}{{{2^n}}}\].
B. \[{u_n} = 3 - \frac{4}{{n + 1}}\].
C. \[{u_n} = {n^2}\].
D. \[{u_n} = \sqrt {n + 2} \].
Cho dãy số $\left( {{u_n}} \right)$, với ${u_n} = {\left( {\frac{{n - 1}}{{n + 1}}} \right)^{2n + 3}}$. Tìm số hạng ${u_{n + 1}}$.
A. ${u_{n + 1}} = {\left( {\frac{{n - 1}}{{n + 1}}} \right)^{2(n + 1) + 3}}$.
B. ${u_{n + 1}} = {\left( {\frac{{n - 1}}{{n + 1}}} \right)^{2(n - 1) + 3}}$.
C. ${u_{n + 1}} = {\left( {\frac{n}{{n + 1}}} \right)^{2n + 3}}$.
D. ${u_{n + 1}} = {\left( {\frac{n}{{n + 1}}} \right)^{2n + 5}}$.
Dãy số này dưới đây là một cấp số cộng?
A.1; 4; 7; 13; 16.
B. 2; 4; 6; 8; 12.
C.0,1; 0,01; 0,001; 0,0001.
D. 3; 5; 7; 9; 11.
Khẳng định nào sau đây là sai?
A. Dãy số $ - \frac{1}{2};\,0;\,\frac{1}{2};\,1;\frac{3}{2};.....$ là một cấp số cộng: ${u_1} = - \frac{1}{2};\,\,d = \frac{1}{2}$.
B. Dãy số $\frac{1}{2};\,\frac{1}{{{2^2}}};\,\frac{1}{{{2^3}}};.....$ là một cấp số cộng:${u_1} = \frac{1}{2};\,\,d = \frac{1}{2}$.
C. Dãy số :\[\;--{\text{ }}2;{\text{ }}--{\text{ }}2;{\text{ }}--{\text{ }}2;{\text{ }}--{\text{ }}2;{\text{ }} \ldots \;\]là cấp số cộng ${u_1} = - 2;\,\,d = 0$.
D. Dãy số: \[0,1;{\text{ }}0,01;{\text{ }}0,001;{\text{ }}0,0001;{\text{ }} \ldots \]không phải là một cấp số cộng.
Ba góc của một tam giác tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo là
A. $20^\circ $ và $70^\circ $.
B. $45^\circ $ và $45^\circ $.
C. $20^\circ $ và $45^\circ $.
D. $30^\circ $ và $60^\circ .$
Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số thứ mười hai bằng 23. Khi đó công sai $d$ của cấp số cộng đã cho bằng bao nhiêu?
A. $d = 2$.
B. $d = 3$.
C. $d = 4$.
D. $d = 5$.
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} \ne 0$ và $q \ne 0$. Đẳng thức nào sau đây là đúng?
A. ${u_7} = {u_4}.\,{q^3}$.
B. ${u_7} = {u_4}.\,{q^4}$.
C. ${u_7} = {u_4}.\,{q^5}$.
D. ${u_7} = {u_4}.\,{q^6}$.
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_n} = 81$ và ${u_{n + 1}} = 9$. Mệnh đề nào sau đây đúng?
A. \[q = \frac{1}{9}\].
B. \[q = 9\].
C. \[q = - 9\].
D. \[q = - \frac{1}{9}\].
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = - 3$ và $q = \frac{2}{3}$. Mệnh đề nào sau đây là đúng?
A. \[{u_5} = - \frac{{27}}{{16}}\].
B. \[{u_5} = - \frac{{16}}{{27}}\].
C. \[{u_5} = \frac{{16}}{{27}}\].
D. \[{u_5} = \frac{{27}}{{16}}\].
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = - 1$ và $q = - \frac{1}{{10}}$. Số $\frac{1}{{{{10}^{103}}}}$ là số hạng thứ mấy của cấp số nhân đã cho?
A. Số hạng thứ 103.
B. Số hạng thứ 104.
C. Số hạng thứ 105.
D. Không là số hạng của cấp số đã cho.
Cho tứ diện $ABCD$. Khẳng định nào sau đây là đúng?
A. $AB$ và $CD$ cắt nhau.
B.Bốn điểm $A,\,\,B,\,\,C,\,\,D$ không đồng phẳng.
C. $AC$ và $BD$ cắt nhau.
D.Bốn điểm $A,\,\,B,\,\,C,\,\,D$ thẳng hàng.
Mệnh đề nào đúng trong các mệnh đề sau?
A. Nếu ba điểm $A,\,\,B,\,\,C$ là ba điểm chung của hai mặt phẳng $(P)$ và $(Q)$ thì $A,\,\,B,\,\,C$ thẳng hàng.
B.Nếu ba điểm $A,\,\,B,\,\,C$ thẳng hàng và hai mặt phẳng $(P)$ và $(Q)$ có điểm chung là $A$ thì $B,\,C$ cũng là hai điểm chung của $(P)$ và $(Q)$.
C.Nếu ba điểm $A,\,\,B,\,\,C$ là ba điểm chung của hai mặt phẳng $(P)$ và $(Q)$ phân biệt thì $A,\,\,B,\,\,C$ không thẳng hàng.
D.Nếu ba điểm $A,\,\,B,\,\,C$ thẳng hàng và $A,\,\,B$ là hai điểm chung của $(P)$ và $(Q)$ thì $\,C$ cũng là điểm chung của $(P)$ và $(Q)$.
Cho tứ diện $ABCD$. Gọi $H,\,\,K$ lần lượt là trung điểm các cạnh $AB,\,\,BC.$ Trên đường thẳng $CD$ lấy điểm $M$ nằm ngoài đoạn $CD$. Thiết diện của tứ diện với mặt phẳng $(HKM)$ là
A. Tứ giác $HKMN$ với $N \in AD$.
B.Hình thang $HKMN$với $N \in AD$ và $HK\,{\text{//}}\,MN$.
C.Tam giác $HKL$ với $L = KM \cap BD$.
D.Tam giác $HKL$ với $L = HM \cap AD$.
Cho hình chóp $S.ABC$. Gọi $L,\,\,M,\,\,N$ lần lượt các điểm trên các cạnh $SA,\,\,SB$ và $AC$ sao cho $LM$ không song song với $AB,\,\,LN$ không song song với $SC$. Mặt phẳng $(LMN)$ cắt các cạnh $AB,\,\,BC,\,\,SC$ lần lượt tại $K,\,\,I,\,\,J$. Ba điểm nào sau đây thẳng hàng?
A. $K,\,\,I,\,\,J$.
B. $M,\,\,I,\,\,J$.
C. $N,\,\,I,\,\,J$.
D. $M,\,\,K,\,\,J$.
Tìm khẳng định đúng trong các khẳng định sau.
A. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó nằm trong mặt phẳng đó.
B. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
C. Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến thì ba giao otuyeesn đó phải đồng quy.
D. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì song song với nhau.
B.Hai mặt phẳng phân biệt không song song thì cắt nhau.
C. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
D.Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $I,\,\,J,\,\,E,\,\,F$ lần lượt là trung điểm của $SA,\,\,SB,\,\,SC,\,\,SD$. Trong các đường thẳng sau, đường thẳng nào không song song với $IJ?$
A. $EF$.
B. $DC$.
C. $AD$.
D. $AB$.
Cho hình chóp $S.ABCD$ có đáy là hình thang với các cạnh đáy là $AB$ và $CD$. Gọi $I,\,\,J$ lần lượt là trung điểm của $AD$ và $BC$; $G$ là trọng tâm của tam giác $SAB.$ Giao tuyến của $(SAB)$ và $(IJG)$ là
A. $SC$.
B.đường thẳng qua $S$ và song song với $AB$.
C.đường thẳng qua $G$ và song song với $DC$.
D.đường thẳng qua $G$ và cắt $BC$.

