Quiz

Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) (Đề 6)

Admin40 câu hỏiToánLớp 12

Bắt đầu ngay

40 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Hỏi hàm số $y = 2 x^{4} + 1$ đồng biến trên khoảng nào?

A. $(0; + \infty)$

B. $(- \infty; - \frac{1}{2})$

C. $(- \infty; 0)$

D. $(- \frac{1}{2}; + \infty)$

2. Nhiều lựa chọn

Số điểm cực trị của hàm số $y = - x^{3} + 3 x^{2} + x + 1$ là

A. 2

B. 3

C. 1

D. 0

3. Nhiều lựa chọn

Tìm giá trị lớn nhất của hàm số $y = - x^{3} + 3 x^{2}$ trên đoạn $[- 2; 1]$

A. $\max_{[- 2; 1]} y = 2$

B. $\max_{[- 2; 1]} y = 0$

C. $\max_{[- 2; 1]} y = 20$

D. $\max_{[- 2; 1]} y = 54$

4. Nhiều lựa chọn

Đồ thị hàm số $y = \frac{2 x - 1}{x + 2}$ có các đường tiệm cận là:

A. y = -2 và x = -2

B. y = 2 và x = -2

C. y = -2 và x = 2

D. y = 2 và x = 2

5. Nhiều lựa chọn

Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào?

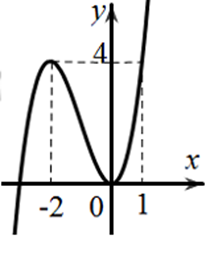
Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào? (ảnh 1)

A. $y = x^{3} + 3 x^{2}$

B. $y = - x^{3} + 3 x^{2}$

C. $y = - x^{3} - 3 x^{2}$

D. $y = x^{3} + 3 x^{2} + 1$

6. Nhiều lựa chọn

Cho biểu thức $P = \sqrt{x^{4} \sqrt[3]{x}}$ với x là số dương khác 1. Khẳng định nào sau đây sai?

A. $P = x \sqrt{x^{2} \sqrt[3]{x}}$

B. $P = x^{2} . \sqrt[3]{x}$

C. $P = x^{\frac{13}{6}}$

D. $P = \sqrt[6]{x^{13}}$

7. Nhiều lựa chọn

Tính giá trị của biểu thức $A = \log_{a} \frac{1}{a^{2}}$ , với a > 0 và $a \neq 1$

A. A = -2

B. $A = - \frac{1}{2}$

C. A = 1

D. $A = \frac{1}{2}$

8. Nhiều lựa chọn

Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp đôi thì thể tích khối hộp tương ứng sẽ:

A. tăng 2 lần.

B. tăng 4 lần.

C. tăng 6 lần.

D. tăng 8 lần.

9. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $A B = 3 a, A C = 4 a$ , SB vuông góc (ABC), $S C = 5 a \sqrt{2}$ . Tính thể tích khối chóp S.ABC theo a.

A. 10a³

B. 30a³

C. $10 a^{3} \sqrt{2}$

D. 5a³

10. Nhiều lựa chọn

Cho hình nón (N) có thiết diện qua trục là một tam giác vuông có cạnh huyền bằng a (cm) . Tính thể tích V của khối nón đó.

A. $V = \frac{a^{3} π}{8} c m^{3}$

B. $V = \frac{a^{3} π}{6} c m^{3}$

C. $V = \frac{a^{3} π}{24} c m^{3}$

D. $V = \frac{a^{3} π}{3} c m^{3}$

11. Nhiều lựa chọn

Tìm tất cả các giá trị của tham số thực m sao cho hàm số $y = \frac{x^{3}}{3} - x^{2} + (2 m - m^{2}) x - 1$ có 2 điểm cực trị.

A. $m \neq 1$

B. $m \in ℝ$

C. m = 1

D. $m \in (- \infty; 1)$

12. Nhiều lựa chọn

Hàm số nào nghịch biến trên R

A. $y = \frac{1}{x}$

B. $y = x^{4} + 5 x^{2}$

C. $y = - x^{3} + 2$

D. $y = \cot x$

13. Nhiều lựa chọn

Cho hàm số $y = - 2 x^{3} + 3 x^{2} + 5$ . Hàm số có giá trị cực tiểu bằng:

A. 5

B. 6

C. 0

D. 1

14. Nhiều lựa chọn

Cho hàm số $y = x^{4} + 4 x^{3} - m$ . Khẳng định nào sau đây là khẳng định sai:

A. Số cực trị của hàm số không phụ thuộc vào tham số m

B. Số cực trị của hàm số phụ thuộc vào tham số m

C. Hàm số có đúng một cực trị

D. Hàm số có đúng một cực tiểu

15. Nhiều lựa chọn

Trong tất cả các hình chữ nhật có chu vi 40 cm. Hình chữ nhật có diện tích lớn nhất có diện tích S là

A. S = 100 cm²

B. S = 400 cm²

C. S = 49 cm²

D. S = 40 cm²

16. Nhiều lựa chọn

Một chất điểm chuyển động theo quy luật $s = - t^{3} + 3 t^{2}$ . Khi đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm (giây) bằng:

A. t = 2

B. t = 0

C. t = 1

D. $[\begin{array}{l} t = 1 \\ t = 2 \end{array}$

17. Nhiều lựa chọn

Cho hàm số y = f(x) thỏa mãn điều kiện $\lim_{x \to + \infty} y = a \in ℝ; \lim_{x \to - \infty} y = + \infty; \lim_{x \to x_{0}^{-}} y = + \infty$ . Chọn mệnh đề sai trong các mệnh đề sau?

A. Đồ thị hàm số y = f(x) có 2 tiệm cận ngang và 1 tiệm cận đứng.

B. Đồ thị hàm số y = f(x) có 1 tiệm cận ngang và 1 tiệm cận đứng.

C. Đồ thị hàm số y = f(x) có tiệm cận ngang y = a.

D. Đồ thị hàm số y = f(x) có tiệm cận đứng x = x_o.

18. Nhiều lựa chọn

Đồ thị hàm số nào sau đây không có đường tiệm cận:

A. $y = \frac{x}{2 x^{2} - 1}$

B. $y = - x$

C. $y = \frac{x - 2}{3 x + 2}$

D. $y = x + 2 - \frac{1}{x - 3}$

19. Nhiều lựa chọn

Biết rằng đường thẳng $y = - 2 x + 2$ cắt đồ thị hàm số $y = x^{3} + x + 2$ tại điểm duy nhất; kí hiệu $x_{0}; y_{0}$ là tọa độ của điểm đó. Tìm $y_{0}$

A. $y_{0} = 2$

B. $y_{0} = 4$

C. $y_{0} = 0$

D. $y_{0} = - 1$

20. Nhiều lựa chọn

Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y = \frac{x + 1}{\sqrt{m x^{2} + 1}}$ có hai tiệm cận ngang.

A. m < 0

B. m = 0

C. m > 0

D. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài

21. Nhiều lựa chọn

Giải phương trình $\log_{4} (x - 1) = 3$

A. x = 63

B. x = 65

C. x = 82

D. x = 80

22. Nhiều lựa chọn

Cho các số thực dương a, b với $a \neq 1$ . Khẳng định nào sau đây là khẳng định đúng?

A. $\log_{a^{2}} (a b) = \frac{1}{2} + \frac{1}{2} \log_{a} b$

B. $\log_{a^{2}} (a b) = 2 + \log_{a} b$

C. $\log_{a^{2}} (a b) = \frac{1}{4} \log_{a} b$

D. $\log_{a^{2}} (a b) = \frac{1}{2} \log_{a} b$

23. Nhiều lựa chọn

Tìm nghiệm của bất phương trình $\log_{\frac{1'}{2}} (3 x - 1) > 3$

A. $x < \frac{3}{8}$

B. $\frac{1}{3} < x < \frac{3}{8}$

C. $x > \frac{3}{8}$

D. $\frac{1}{3} < x < \frac{5}{8}$

24. Nhiều lựa chọn

Cho các hàm số sau:

(1) $y = {(x - 2)}^{π}$ . (2) $y = {(x - 2)}^{- 2}$ . (3) $y = {(x - 2)}^{\frac{1}{3}}$ .

(4) $y = \frac{1}{x - 2}$ . (5) $y = \frac{1}{\sqrt{x - 2}}$ . (6) $y = \sqrt[3]{x - 2}$ .

Hỏi có bao nhiêu hàm số có tập xác định là $D = (2; + \infty)$ ?

A. 1

B. 2

C. 3

D. 4

25. Nhiều lựa chọn

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D', có cạnh đáy bằng a. Góc giữa A'C và đáy (ABCD) bằng 45^o . Tính thể tích của khối lăng trụ ABC.A'B'C' theo a.

A. $\frac{a^{3} \sqrt{3}}{2}$

B. $a^{3} \sqrt{3}$

C. $a^{2} \sqrt{2}$

D. $\frac{a^{3} \sqrt{2}}{2}$

26. Nhiều lựa chọn

Cho hình nón (N) có đỉnh O và tâm của đáy là H. $(α)$ là mặt phẳng qua O . Nên kí hiệu $d (H; (α))$ là khoảng cách từ H đến mặt phẳng $(α)$ . Biết chiều cao và bán kính đáy của hình nón lần lượt là h, r . Khẳng định nào sau đây là sai?

A. Nếu $d (H, (α)) > \frac{r h}{\sqrt{r^{2} + h^{2}}}$ thì $(α) \cap (N) = \emptyset$

B. Nếu $d (H, (α)) < \frac{r h}{\sqrt{r^{2} + h^{2}}}$ thì $(α) \cap (N)$ là tam giác cân

C. Nếu $d (H, (α)) = \frac{r h}{\sqrt{r^{2} + h^{2}}}$ thì $(α) \cap (N)$ là đoạn thẳng.

D. Nếu $d (H, (α)) > \frac{r h}{\sqrt{r^{2} + h^{2}}}$ thì $(α) \cap (N)$ là một điểm

27. Nhiều lựa chọn

Cho khối nón (N) đỉnh O có bán kính đáy là r . Biết thể tích khối nón (N) là V_o. Tính diện tích S của thiết diện qua trục của khối nón.

A. $S = \frac{V_{0}}{π r}$

B. $S = \frac{3 V_{0}}{π r^{2}}$

C. $S = \frac{3 V_{0}}{π r}$

D. $S = \frac{3 π r}{V_{0}}$

28. Nhiều lựa chọn

Cho khối chóp tam giác S.ABC có (SBA) và (SBC) cùng vuông góc với (ABC) , đáy ABC là tam giác đều cạnh a, SC bằng $a \sqrt{7}$ . Đường cao của khối chóp S.ABC bằng

A. a

B. $2 a \sqrt{2}$

C. $a \sqrt{6}$

D. $a \sqrt{5}$

29. Nhiều lựa chọn

Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy là tam giác vuông cân tại A cạnh AB bằng $a \sqrt{3}$ , góc giữa A'C và (ABC) bằng 45^o . Khi đó đường cao của lăng trụ bằng:

A. a

B. $a \sqrt{3}$

C. $a \sqrt{2}$

D. 3a

30. Nhiều lựa chọn

Cho hình chóp S.ABCD có ABCD là hình chữ nhật, $A B = 2 a, B C = a, S A = a,$ $S B = a \sqrt{3}$ , (SAB) vuông góc với (ABCD) . Khi đó thể tích của khối chóp SABCD bằng

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $\frac{a^{3} \sqrt{3}}{6}$

C. $a^{3} \sqrt{3}$

D. $2 a^{3} \sqrt{3}$

31. Nhiều lựa chọn

Tìm giá trị nhỏ nhất của hàm số $y = \sin^{3} x - 3 \sin x$ trên đoạn $[0; \frac{π}{3}]$

A. -2

B. 0

C. $- \frac{9 \sqrt{3}}{8}$

D. $- \frac{5 \sqrt{2}}{4}$

32. Nhiều lựa chọn

Cho hàm số $y = m x^{4} + (m^{2} - 9) x^{3} + 10$ . Tìm m để hàm số có 3 điểm cực trị.

A. $[\begin{array}{l} m < - 1 \\ 0 < m < 2 \end{array}$

B. $[\begin{array}{l} m < - 3 \\ 0 < m < 3 \end{array}$

C. $[\begin{array}{l} m < 3 \\ - 1 < m < 0 \end{array}$

D. $[\begin{array}{l} m < 0 \\ 1 < m < 3 \end{array}$

33. Nhiều lựa chọn

Cho $\log_{2} 5 = a; \log_{3} 5 = b$ . Tính $\log_{6} 1080$ theo a và b ta được:

A. $\frac{a b + 1}{a + b}$

B. $\frac{2 a + 2 b + a b}{a + b}$

C. $\frac{3 a + 3 b + a b}{a + b}$

D. $\frac{2 a - 2 b + a b}{a + b}$

34. Nhiều lựa chọn

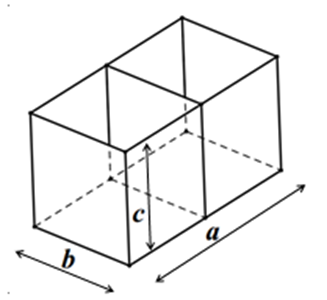
Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 1,296 m³. Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình hộp chữ nhật với 3 kích thước a, b, c như hình vẽ. Hỏi người thợ phải thiết kế các kích thước a, b, c bằng bao nhiêu để đỡ tốn kính nhất, giả sử độ dầy của kính không đáng kể. Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 1,296 m3. (ảnh 1)

A. $a = 3, 6 m; b = 0, 6 m; c = 0, 6 m$

B. $a = 2, 4 m; b = 0, 9 m; c = 0, 6 m$

C. $a = 1, 8 m; b = 1, 2 m; c = 0, 6 m$

D. $a = 1, 2 m; b = 1, 2 m; c = 0, 9 m$

35. Nhiều lựa chọn

Cho hình chóp S.ABCD có hình chiếu vuông góc của S trên mặt đáy ABCD là điểm I thuộc AD sao cho $A I = 2 I D, S B = \frac{a \sqrt{7}}{2}$ , ABCD là hình vuông có cạnh bằng a. Khi đó thể tích của khối chóp S.ABCD bằng:

A. $\frac{a^{3} \sqrt{2}}{6}$

B. $\frac{a^{3} \sqrt{11}}{12}$

C. $\frac{a^{3} \sqrt{11}}{18}$

D. $\frac{a^{3} \sqrt{2}}{18}$

36. Nhiều lựa chọn

Tìm tất cả các giá trị của m để đường thẳng y = m cắt đồ thị hàm số $y = 2 x^{2} |x^{2} - 2|$ tại 6 điểm phân biệt.

A. 0 < m < 2

B. 0 < m < 1

C. 1 < m < 2

D. Không tồn tại m

37. Nhiều lựa chọn

Có tất cả bao nhiêu giá trị của tham số m sao cho hàm số $y = m x^{3} + 3 x^{2} + m^{2}, (m \neq 0)$ đồng biến trên khoảng (a;b) và nghịch biến trên các khoảng $(- \infty; a), (b; + \infty)$ sao cho $|a - b| = 2$

A. 0

B. 1

C. 2

D. Vô số m.

38. Nhiều lựa chọn

Cho $a = 10^{\frac{m}{n - \log b}}; b = 10^{\frac{m}{n - \log c}}$ với a, b, c, m, n là các số nguyên sao cho các biểu thức có nghĩa. Tính biểu thức logc theo loga

A. $\log c = \frac{(m^{2} - n) \log a - m n}{n \log a - m}$

B. $\log c = \frac{(n^{2} - m) \log a - m n}{n \log a - m}$

C. $\log c = \frac{(n^{2} - m) \log a - n}{n \log a - m n}$

D. $\log c = \frac{(m^{2} - n) \log a - m n}{m \log a - n}$

39. Nhiều lựa chọn

Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông. Độ dài $S B = \frac{a \sqrt{5}}{2}$ . Góc giữa mặt bên và mặt đáy bằng 60^o . Tính thể tích khối nón có đỉnh S và đáy là đường tròn nội tiếp hình vuông ABCD .

A. $\frac{a^{3} π \sqrt{3}}{24}$

B. $\frac{a^{3} π \sqrt{3}}{8}$

C. $\frac{a^{3} π \sqrt{3}}{27}$

D. $a^{3} π \sqrt{3}$

40. Nhiều lựa chọn

Cho hình lập phương ABCD.A'B'C'D' cạnh a . Gọi M, P lần lượt là trung điểm của AA' và B'C'. N là điểm thuộc cạnh A'D' thỏa mãn 3A'N = ND'. Tính diện tích S_o của thiết diện của (MNP) với hình lập phương.

A. $S_{0} = \frac{3 a^{2} \sqrt{85}}{32}$

B. $S_{0} = \frac{15 a^{2}}{32}$

C. $S_{0} = \frac{3 a^{2} \sqrt{21}}{8}$

D. $S_{0} = \frac{3 a^{2} \sqrt{21}}{16}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube