Quiz

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 6

Admin50 câu hỏiToánLớp 12

Bắt đầu ngay

50 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hàm số F (x) là một nguyên hàm của hàm số f (x) và C là một hằng số. Mệnh đề nào dưới đây đúng?

A. F '(x) = f '(x) + C;

B. |F (x) + C|' = f (x);

C. f '(x) = F (x) + C;

D. F (x) = f (x) + C.

2. Nhiều lựa chọn

Trong không gian Oxyz, tâm và bán kính của mặt cầu (S): (x - 1)² + y² + (z + 2)² = 4 là

A. I(1; 0; -2), R = 2;

B. I(1; 0; 2), R = 2;

C. I(-1; 0; 2), R = 4;

D. I(1; 0; -2), R = 4.

3. Nhiều lựa chọn

Họ nguyên hàm của hàm số $f (x) = \frac{1}{x}$ là

A. -ln|x| + C;

B. ln|x| + C;

C. $- \frac{1}{x^{2}} + C;$

D. $\frac{1}{x^{2}} + C .$

4. Nhiều lựa chọn

Giá trị của $\int_{0}^{1} (2 x + e^{x}) d x$ bằng

A. e - 1;

B. -e;

C. e;

D. e + 1.

5. Nhiều lựa chọn

Trong không gian Oxyz, cho hai vectơ $\vec{a} = (- 1; 2; - 3)$ và $\vec{b} = (- 2; 4; 5)$ . Giá trị của $\vec{a} . \vec{b}$ bằng

A. -16;

B. 16;

C. -5;

D. 5.

6. Nhiều lựa chọn

Trong không gian Oxyz, đường thẳng đi qua điểm A(0; 1; 1) và song song với đường thẳng $Δ : \{\begin{matrix} x = 1 + t \\ y = 2 - 3 t \\ z = 2 + 4 t \end{matrix}$ có phương trình là

A. $\frac{x - 1}{- 1} = \frac{y}{- 3} = \frac{z - 1}{4};$

B. $\frac{x}{- 1} = \frac{y - 1}{- 3} = \frac{z - 1}{4};$

C. $\frac{x}{- 1} = \frac{y - 1}{3} = \frac{z - 1}{4};$

D. $\frac{x}{1} = \frac{y - 1}{- 3} = \frac{z - 1}{4} .$

7. Nhiều lựa chọn

Trong không gian Oxyz, phương trình của mặt phẳng đi qua điểm M(-1; 2; 0) và có vectơ pháp tuyến $\vec{n} = (4; 0; - 5)$ là

A. 4x - 5z + 4 = 0;

B. 4x - 5z - 4 = 0;

C. 4x - 5y + 4 = 0;

D. 4x - 5y - 4 = 0.

8. Nhiều lựa chọn

Nghiệm của phương trình z² - 2z + 5 = 0 là

A. -2 + i và -2 - i;

B. 2 + i và 2 - i;

C. -1 + 2i và -1 - 2i;

D. 1 + 2i và 1 - 2i.

9. Nhiều lựa chọn

Cho số phức z thỏa mãn 2z + (1 + i) = (5 - 2i)(1 - i). Môđun của số z bằng

A. $\sqrt{15};$

B. $\sqrt{17};$

C. 15;

D. 17.

10. Nhiều lựa chọn

Số phức liên hợp của số phức z = 2021 - 2022i là

A. -2021 - 2022i;

B. 2022 + 2021i;

C. 2021 + 2022i;

D. -2021 + 2022i.

11. Nhiều lựa chọn

Trong không gian Oxyz, phương trình mặt cầu có tâm I(-1; -2; 3) và bán kính R = 2 là

A. (x + 1)² + (y + 2)² + (z - 3)² = 2;

B. (x - 1)² + (y - 2)² + (z + 3)² = 2;

C. (x - 1)² + (y - 2)² + (z + 3)² = 4;

D. (x + 1)² + (y + 2)² + (z - 3)² = 4.

12. Nhiều lựa chọn

Trong không gian Oxyz, khoảng cách từ điểm M(3; 4; 5) đến mặt phẳng (P): 3x - 4y + 12z - 14 = 0 bằng

A. 3;

B. 6;

C. $\frac{85}{13};$

D. $\frac{53}{13} .$

13. Nhiều lựa chọn

Cho hàm số f (x) liên tục trên ℝ và $\int_{- 2}^{4} f (x) d x = 12$ . Giá trị của $\int_{1}^{2} f (6 x - 8) d x$ bằng

A. -2;

B. -72;

C. 2;

D. 72.

14. Nhiều lựa chọn

Cho hàm số f (x) liên tục trên đoạn [a; b] và số thực k tùy ý khác 0. Mệnh đề nào dưới đây đúng?

A. $\int_{a}^{b} k f (x) d x = k \int_{a}^{b} f (x) d x;$

B. $\int_{a}^{b} k f (x) d x = k \int_{b}^{a} f (x) d x;$

C. $\int_{a}^{b} k f (x) d x = \int_{a}^{b} f (k x) d x;$

D. $\int_{a}^{b} k f (x) d x = \int_{b}^{a} f (k x) d x .$

15. Nhiều lựa chọn

Nếu đặt $t = \sqrt{x^{2} + 1}$ thì $\int x \sqrt{x^{2} + 1} d x$ trở thành

A. $\int 2 t d t;$

B. $\int t d t;$

C. $\int 2 t^{2} d t;$

D. $\int t^{2} d t .$

16. Nhiều lựa chọn

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = 1 - x², trục hoành và hai đường thẳng x = -1, x = 1. Thể tích của khối tròn xoay được tạo thành khi quay hình (H) quanh trục hoành bằng

A. $\frac{4}{3};$

B. $\frac{16 π}{15};$

C. $\frac{16}{15};$

D. $\frac{4 π}{3} .$

17. Nhiều lựa chọn

Cho hàm số y = f (x) liên tục trên [a; b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức

A. $S = \int_{a}^{b} f (x) d x;$

B. $S = π \int_{a}^{b} {[f (x)]}^{2} d x;$

C. $S = \int_{a}^{b} |f (x)| d x;$

D. $S = \int_{b}^{a} |f (x)| d x .$

18. Nhiều lựa chọn

Hình phẳng giới hạn bởi đồ thị hàm số y = x³, trục Ox và hai đường thẳng x = -2, x = 0 có diện tích bằng

A. 16;

B. 4;

C. 2;

D. 8.

19. Nhiều lựa chọn

Biết z₁ = 2 - 3i là một nghiệm của phương trình z² + bz + c = 0 với b, c là các số thực. Giá trị của b + c bằng

A. 9;

B. -5;

C. -1;

D. 13.

20. Nhiều lựa chọn

Gọi z₁, z₂, z₃, z₄ là các nghiệm của phương trình z⁴ - 2z² - 8 = 0. Giá trị của |z₁|² + |z₂|² + |z₃|² + |z₄|² bằng

A. 16;

B. 8;

C. 4;

D. 12.

21. Nhiều lựa chọn

Phần ảo của số phức z = 2 + i là

A. -2;

B. 1;

C. 2;

D. -1.

22. Nhiều lựa chọn

Trong không gian Oxyz, đường thẳng đi qua điểm A(-2; 3; 5) và vuông góc với mặt phẳng (P): x - 2y + 2z + 1 = 0 có phương trình là

A. $\{\begin{matrix} x = 2 + t \\ y = - 3 - 2 t \\ z = - 5 + 2 t \end{matrix};$

B. $\{\begin{matrix} x = - 1 - 2 t \\ y = 2 + 3 t \\ z = - 2 + 5 t \end{matrix};$

C. $\{\begin{matrix} x = - 2 + t \\ y = 3 - 2 t \\ z = 5 + 2 t \end{matrix};$

D. $\{\begin{matrix} x = - 1 - 2 t \\ y = 2 + 3 t \\ z = - 2 + 5 t \end{matrix} .$

23. Nhiều lựa chọn

Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt cầu?

A. x² + y² - z² - 2x - 2y - 2z - 1 = 0;

B. x² + y² + 2z² - 2x - 2y - 2z - 1 = 0;

C. x² + y² + z² - 2x - 2y - 2z - 1 = 0;

D. x² + y² + z² - 2x - 2y - 2z + 3 = 0;

24. Nhiều lựa chọn

Cho hai số thực x, y thỏa mãn x - 2y + (3x + y)i = 2 + 13i. Giá trị của x - 2y bằng

A. -6;

B. -2;

C. 6;

D. 2.

25. Nhiều lựa chọn

Trong không gian Oxyz, cho ba điểm A(2; 1; -1), B(3; 2; -1) và C(1; 1; 2). Một vectơ pháp tuyến của mặt phẳng (ABC) là

A. (3; -3; 1);

B. (3; 3; 1);

C. (-3; 3; 1);

D. (3; -3; -1).

26. Nhiều lựa chọn

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = -x² + 4 và y = -x + 2 bằng

A. $\frac{8}{3};$

B. $\frac{9}{2};$

C. 9;

D. $\frac{5}{7} .$

27. Nhiều lựa chọn

Trong không gian Oxyz, phương trình mặt phẳng đi qua hai điểm A(-1; 2; 3), B(1; 4; 2) và vuông góc với mặt phẳng (P): x - y + 2z + 1 = 0 là

A. 3x - y - 2z + 11 = 0;

B. 5x - 3y - 4z + 23 = 0;

C. 3x + 5y + z - 10 = 0;

D. 3x - 5y - 4z + 25 = 0.

28. Nhiều lựa chọn

Trong mặt phẳng Oxy, điểm M như hình vẽ bên dưới biểu diễn cho số phức nào sau đây?

Media VietJack

A. -4 - 2i;

B. -2 - 4i;

C. -2 + 4i;

D. 4 - 2i.

29. Nhiều lựa chọn

Giá trị của $\int_{0}^{\frac{π}{2}} x \cos x d x$ bằng

A. $\frac{π}{2} - 1;$

B. $\frac{π + 1}{2};$

C. $\frac{π - 1}{2};$

D. $\frac{π}{2} + 1.$

30. Nhiều lựa chọn

Một ô tô đang chạy với vận tốc 8 m/s thì người lái xe đạp phanh. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v (t) = -2t + 8 (m/s), trong đó t là thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét?

A. 6 m;

B. 16 m;

C. 32 m;

D. 8 m.

31. Nhiều lựa chọn

Cho hai số phức z₁ = 2 - 3i và z₂= 4 - 6i. Số phức z₁ - z₂ là

A. 2 + 3i;

B. -2 - 3i;

C. -2 + 3i;

D. 6 - 9i.

32. Nhiều lựa chọn

Họ nguyên hàm của hàm số f (x) = xe^x là

A. -xe^x + e^x + C;

B. -xe^x - e^x + C;

C. xe^x - e^x + C;

D. xe^x + e^x + C.

33. Nhiều lựa chọn

Cho hàm số y = f (x) liên tục trên [-2; 2] và có đồ thị như hình vẽ bên dưới. Gọi S là diện tích của hình phẳng được giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = -2, x = 2.

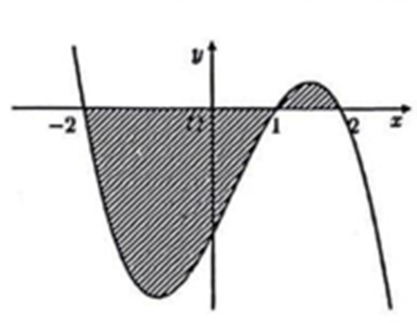
Media VietJack

Mệnh đề nào dưới đây đúng?

A. $S = \int_{- 2}^{1} f (x) d x - \int_{1}^{2} f (x) d x;$

B. $S = - \int_{- 2}^{1} f (x) d x + \int_{1}^{2} f (x) d x;$

C. $S = - \int_{- 2}^{1} f (x) d x - \int_{1}^{2} f (x) d x;$

D. $S = \int_{- 2}^{1} f (x) d x + \int_{1}^{2} f (x) d x .$

34. Nhiều lựa chọn

Trong không gian Oxyz, cho điểm M(6; -6; 6) và đường thẳng $Δ : \frac{x - 8}{2} = \frac{y + n}{4} = \frac{z - m}{- 3}$ với m, n là các tham số thực. Biết rằng điểm M thuộc đường thẳng D, giá trị m - n bằng

A. -1;

B. -5;

C. 1;

D. 5.

35. Nhiều lựa chọn

Trong không gian Oxyz, cho hai điểm A(1; 3; -5) và B(3; 1; -3). Tọa độ của vectơ $\vec{A B}$ là

A. (4; 4; -8);

B. (2; 2; -4);

C. (2; -2; 2);

D. (1; -1; 1).

36. Nhiều lựa chọn

Họ nguyên hàm của hàm số f (x) = 3x² + 2x + 1 là

A. 3x³ + x² + x + C;

B. x³ + x² + x + C;

C. x³ + x² + C;

D. x³ + 2x² + x + C.

37. Nhiều lựa chọn

Môđun của số phức z = -3 + 4i bằng

A. 5;

B. 25;

C. 1;

D. $\sqrt{7} .$

38. Nhiều lựa chọn

Phần thực của số phức z = (4 - i) + (1 + 4i) là

A. -3;

B. 3;

C. -5;

D. 5.

39. Nhiều lựa chọn

Trong không gian Oxyz, đường thẳng đi qua điểm A(0; 1; 1), vuông góc với hai đường thẳng $Δ_{1} : \frac{x - 3}{- 2} = \frac{y - 6}{2} = \frac{x - 1}{3}$ và $Δ_{2} : \{\begin{matrix} x = 2 t \\ y = - t \\ z = 2 + 3 t \end{matrix}$ có phương trình là

A. $\frac{x}{7} = \frac{y + 1}{8} = \frac{z + 1}{- 2};$

B. $\frac{x - 1}{7} = \frac{y}{8} = \frac{z - 1}{- 2};$

C. $\frac{x}{7} = \frac{y - 1}{8} = \frac{z - 1}{- 2};$

D. $\frac{x}{7} = \frac{y - 1}{- 8} = \frac{z - 1}{- 2} .$

40. Nhiều lựa chọn

Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng (P): 3x - 2y + 2z + 1 = 0 có tọa độ là

A. (3; -2; 2);

B. (3; 2; 2);

C. (3; -2; 1);

D. (3; 2; 1).

41. Nhiều lựa chọn

Trong không gian Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 1}{2} = \frac{y}{1} = \frac{z + 2}{- 1}$ và $d_{2} : \frac{x - 1}{1} = \frac{y + 2}{3} = \frac{z - 2}{- 2}$ . Gọi D là đường thẳng song song với mặt phẳng (P): x + y + z - 2022 = 0 và cắt hai đường thẳng d₁, d₂ lần lượt tại A, B sao cho độ dài đoạn thẳng AB ngắn nhất. Phương trình đường thẳng D là

A. $\{\begin{matrix} x = 6 - t \\ y = \frac{5}{2} \\ z = - \frac{9}{2} + t \end{matrix};$

B. $\{\begin{matrix} x = 6 - 2 t \\ y = \frac{5}{2} + t \\ z = - \frac{9}{2} + t \end{matrix};$

C. $\{\begin{matrix} x = 6 \\ y = \frac{5}{2} - t \\ z = - \frac{9}{2} + t \end{matrix};$

D. $\{\begin{matrix} x = \frac{9}{5} + 3 t \\ y = \frac{2}{5} + 6 t \\ z = - \frac{12}{5} + 10 t \end{matrix} .$

42. Nhiều lựa chọn

Biết rằng $\int \cos^{2} x d x = \frac{a x + b \sin 2 x}{m} + C$ với a, b và m là các số nguyên dương, C là hằng số. Giá trị của $\frac{a + b}{m}$ bằng

A. $\frac{3}{2};$

B. $\frac{4}{3};$

C. $\frac{5}{4};$

D. $\frac{3}{4} .$

43. Nhiều lựa chọn

Cho hàm số f (x) xác định trên $ℝ \ \{\frac{1}{2}\}$ và $f' (x) = \frac{1}{2 x - 1}$ thỏa mãn $f (2) = 3 + \frac{1}{2} \ln 3$ . Giá trị của f (3) bằng

A. $\frac{1}{2} \ln 5 + 3;$

B. -2ln 5 + 5;

C. 2ln 5 + 3;

D. $\frac{1}{2} \ln 5 + 5.$

44. Nhiều lựa chọn

Trong mặt phẳng Oxy, biết rằng tập hợp điểm biểu diễn của số phức z thỏa mãn |z - 6i + 8| = 25 là một đường tròn tâm I(a; b). Giá trị của a + b bằng

A. 2;

B. -2;

C. 14;

D. -14.

45. Nhiều lựa chọn

Cho hàm số f (x) liên tục trên ℝ thỏa mãn $f (x) = x^{2} + \int_{1}^{2} x f (x) d x$ . Giá trị của $\int_{0}^{2} x f (x) d x$ bằng

A. -11;

B. 11;

C. -7;

D. 19.

46. Nhiều lựa chọn

Trong không gian Oxyz, cho đường thẳng $d : \frac{x}{1} = \frac{y - 1}{1} = \frac{z - 2}{1}$ , mặt phẳng (P): 2x - z - 4 = 0 và mặt phẳng (Q): x - 2y - 2 = 0. Mặt cầu (S) có tâm thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P) và (Q). Bán kính của mặt cầu (S) bằng

A. $\sqrt{3};$

B. 5;

C. 3;

D. $\sqrt{5} .$

47. Nhiều lựa chọn

Cho hai số phức z, w thỏa mãn |w - i| = 2 và z + 2 = iw. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Giá trị M + m bằng

A. 4;

B. 2;

C. 5;

D. 6.

48. Nhiều lựa chọn

Trong không gian Oxyz, gọi S là tập hợp các giá trị nguyên của tham số m sao cho phương trình x² + y² + z² - 2(m + 2)x + 4my - 2mz + 7m² - 1 = 0 là phương trình mặt cầu. Số phần tử của S là

A. 5;

B. 7;

C. 4;

D. 6.

49. Nhiều lựa chọn

Cho hàm số f (x) liên tục trên [-2; 3] và đồ thị của y = f '(x) như hình vẽ bên dưới.

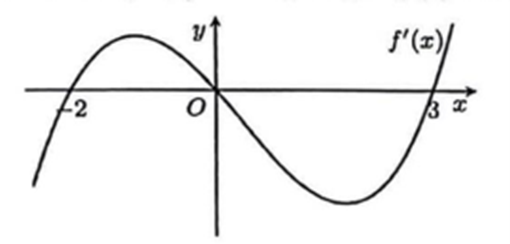
Media VietJack

Mệnh đề nào sau đây đúng?

A. f (-2) > f (0) > f (3);

B. f (0) > f (-2) > f (3);

C. f (0) > f (3) > f (-2);

D. f (3) > f (0) > f (-2).

50. Nhiều lựa chọn

Ông Năm có một khu đất dạng hình chữ nhật với chiều dài là 16 m và chiều rộng là 8 m. Ông Năm trồng rau sạch trên một mảnh vườn được giới hạn bởi hai parabol. Biết rằng mỗi parabol có đỉnh là trung điểm của một cạnh dài và đi qua hai điểm đầu mút của cạnh dài đối diện (phần gạch sọc như hình vẽ minh họa).

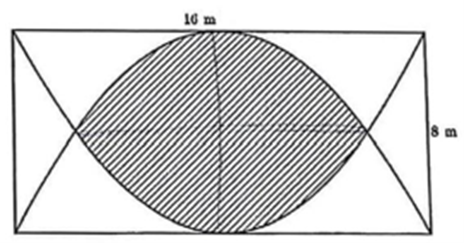
Media VietJack

Biết chi phí trồng rau là 45 000 đồng/m². Hỏi ông Năm cần bao nhiêu tiền (làm tròn đến hàng nghìn) để trồng rau trên phần mảnh vườn đó?

A. 2159000 đồng;

B. 2715000 đồng;

C. 3322000 đồng;

D. 1358000 đồng.

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube