50 CÂU HỎI
Nghịch đảo của số phức z = 2 -i bằng
A.
B.
C.
D.
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = 2x, y = 0, x = -1, x = 3. Mệnh đềnào dưới đây đúng?
A.
B.
C.
D.
Số phức z = (2 + 3i) - (5 - i) có phần ảo bằng
A. 4i;
B. 4;
C. 2i;
D. 2.
Cho và . Tính
A. -4;
B. -16;
C. 16;
D. 4.
Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
A. (2; 1; 3);
B. (1; -2; 0);
C. (1; 2; 0);
D. (2; -1; 3).
Cho hai hàm số f (x), g (x) liên tục trên ℝ. Khẳng định nào sau đây sai?
A.
B.
C.
D.
Tìm họ nguyên hàm của hàm số f (x) = 2+ 2sin x.
A. 2x+ sin2 x +C;
B. 2x-2cos x +C;
C. x2+ sin2x +C;
D. 2x+2cos x +C.
Trong không gian Oxyz, cho hai vectơ và . Tính
A. 2;
B. 0;
C. 1;
D. 4.
Trong mặt phẳng tọa độ Oxy, điểm biểu diễn số phức z = −4− 5i có tọa độ là
A. (-4; 5);
B. (5; -4);
C. (4; -5);
D. (-4; -5).
Biết .Trong các khẳng định sau, khẳng định nào đúng?
A.
B.
C.
D.
Trong không gian Oxyz , phương trình mặt phẳng đi qua 3 điểmA(2;0;0), B(0; -3;0), C(0;0;5) là
A.
B.
C.
D.
Cho hai số phức z1 = 3 -7i và z2 = 2 - 3i. Tìm số phức z = z1 – z2.
A. z = 5 - 4i;
B. z = 5 - 10i;
C. z = 1 - 10i;
D. z = 1 - 4i.
Gọi z0 là nghiệm phức có phần ảo âm của phương trình z2 + z + 1 = 0. Trên mặt phẳng tọađộ, điểm biểu diễn số phức z0 là
A.
B.
C.
D.
Trong không gian Oxyz, đường thẳng đi qua điểm nào dưới đây?
A. Q(1; 0; -2);
B. P(1; 0; 2);
C. N(2; 3; 1);
D. M(-1; 0; 2).
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và haiđường thẳng x= - 2, x =1 như hình vẽ dưới. Khẳng định nào sau đây đúng
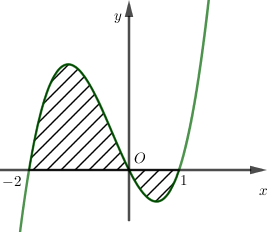
A.
B.
C.
D.
Trong không gian Oxyz, cho đường thẳng D đi qua điểm M (2;1; −1)và có một vectơ chỉphương . Phương trình tham số của D là
A.
B.
C.
D.
Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng (P): x -2y+ z -3 = 0 có tọađộ là
A. (1; -2; 1);
B. (1; 1; -3);
C. (-2; 1; -3);
D. (1; -2; -3).
Tìm phần thực của số phức z biết (2+ i)z = 1- 3i.
A.
B.
C.
D. -1
Cho hình phẳng (H) giới hạn bởi các đường y = 3 - x2, y = 0, x = -2, x = 0. Gọi V là thểtích khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox. Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Số phức liên hợp của số phức z = -2- 5i là
A.
B.
C.
D.
Tìm họ nguyên hàm của hàm số trên khoảng
A.
B.
C.
D.
Biết . Tính S = a -b + c.
A. 3;
B. 1;
C. 4;
D. 2.
Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng (a): 2x - 2y + z - 4 = 0 và(β): 4x - 4y + 2z - 3 = 0 bằng
A.
B.
C.
D.
Gọi x, y là các số thực thỏa mãn (1 - 3i)x - 2y + (1 + 2y)i = -3 + 6i. Tính 2x - y.
A. -1;
B. 1;
C. 3;
D. -3.
Tìm một nguyên hàm của hàm số
A.
B.
C.
D.
Trong không gian Oxyz, đường thẳng d đi qua điểm A(1; −2;1) và vuông góc với mặtphẳng (P): x - 2y + 3z - 1 = 0 có phương trình là
A.
B.
C.
D.
Gọi z1, z2 là hai nghiệm phức của phương trình z2 - 2z +7 = 0. Tính P = |z1|2 + |z2|2.
A. 4;
B. 2;
C. 14;
D. 1.
Trong không gian Oxyz, cho ba điểm A(1; -2;1), B(-1; 3;3), C(0; −3; 1). Một véctơ pháptuyến của mặt phẳng (ABC) là
A. (-2; 3; -7);
B. (2; 2; 7);
C. (2; -2; -7);
D. (2; -2; 7).
Cho hàm số f (x) có đạo hàm trên ℝ, f (-1) = -2, f (0) = 3. Tính
A. -5;
B. 1;
C. 5;
D. -1.
Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức liên hợp của số phứcz = 3-i?
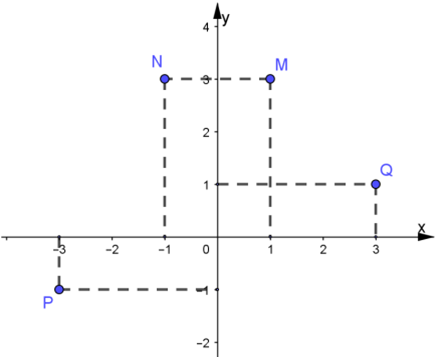
A. N;
B. Q;
C. P;
D. M.
Tìm số phức z thỏa mãn
A.
B.
C.
D.
Trong không gian Oxyz, mặt cầu(S): (x -1)2 + (y + 2)2 + z2 = 9 có tâm I, bán kính R lầnlượt là
A. I(-1; 2; 0), R = 9;
B. I(1; -2; 0), R = 3;
C. I(-1; 2; 0), R = 3;
D. I(1; -2; 0), R = 9.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số y = 2x - x2 và y = 2 - x.
A.
B.
C.
D.
Cho số phức z có phần thực bằng -3 và phần ảo bằng 5. Modul của số phức 2-iz là
A.
B. 58;
C.
D. 4.
Cho hình phẳng D giới hạn bởi đường cong , trục hoành và đường thẳng x = 9.Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành.
A.
B.
C.
D.
Cho số phức z thỏa mãn |z - 2 + i| = |z + 2i|. Trong mặt phẳng phức, tập hợp các điểm biểudiễn số phức z là đường thẳng có phương trình nào sau đây?
A. 4x + 2y - 1 = 0;
B. 2x + 2y - 1 = 0;
C. 4x - 2y + 1 = 0;
D. - 4x - 2y = 0.
Cho số phức z thỏa mãn . Tính môđun của số phức .
A.
B.
C.
D.
Biết 1 - 2i là một nghiệm của phương trình z2 + az + b = 0, a, b Î ℝ. Tính a - b.
A. 7;
B. 3;
C. -3;
D. -7.
Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số ; y = x - 2 và trục hoành.
A.
B.
C.
D.
Trong không gian Oxyz, cho đường thẳng và điểm
A(1; -2;0). Tìmbán kính của mặt cầu có tâm I nằm trên d, đi qua A và tiếp xúc với mặt phẳng (P): 2x - 2y + z - 5 = 0.
A. R = 3;
B. R = 4;
C. R = 1;
D. R = 2.
Cho F (x) là một nguyên hàm của hàm số trên (-¥;2) và F(2- e) = 1. TìmF (x).
A. F (x) = - ln (x - 2) + 2;
B. F (x) = - ln |2 - x| + 1;
C. F (x) = - ln (2 - x) + 2;
D. F (x) = - ln (x - 2) - 2;
Cho hàm số f (x) liên tục trên ℝ thỏa mãn và . Tính
A. I = -14;
B. I = -10;
C. I = 14;
D. I = 10.
Cho là một nguyên hàm của hàm số . Tìm họ nguyên hàm của hàm số
A.
B.
C.
D.
Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A(1; -2; -2), cắt trục Oy, vàsong song với mặt phẳng (P): 2x+ y -4z+ 1 = 0. Viết phương trình tham số của đường thẳng d.
A.
B.
C.
D.
Trong không gianOxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x - 4y + 2z - 3 = 0. Viết phươngtrình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.
A. 2y + z = 0;
B. 2x + y = 0;
C. 2x - y = 0;
D. 2x + y + z = 0.
Cho hàm số f (x) thỏa mãn f (1) = 2 và . Tính f (2).
A. 2
B.
C. 9
D.
Trong không gian Oxyz, cho điểm M(1; -1;2) và hai đường thẳng . Đường thẳng D đi qua M và cắt cả hai đường thẳng d1, d2 có véc tơ chỉphương là . Tính a + b.
A. a + b = 1;
B. a + b = -2;
C. a + b = 2;
D. a + b = -1.
Cho hàm số y = f (x) có đạo hàm liên tục trên ℝthỏa mãn với mọi xÎℝ và f (0) = 0. Tính
A.
B.
C.
D.
Cho số phức z thõa mãn |z - 1 + i| = 2. Tìm giá trị lớn nhất của biểu thứcP = |z + 2 - i|2 + |z - 2 - 3i|2.
A.
B.
C.
D.
Trong không gian Oxyz , cho ba điểm A(2; -2;4), B(-3;3; -1), C(−1; −1; −1) và mặtphẳng (P): 2x - y+ 2z + 8 = 0. Xét điểm M thay đổi thuộc (P), tìm giá trị nhỏ nhất của biểu thứcT = 2MA2 + MB2- MC2.
A. 102;
B. 35;
C. 105;
D. 30.


