50 CÂU HỎI
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \frac{2}{{ - x + 3}}?\)
A. \(x = - 2.\)
B. \(y = - 2.\)
C. \(y = 0.\)
D. \(x = 3.\)
Cho hai số thực dương \(a,b.\) Rút gọn biểu thức \[\] ta thu được \(A = {a^m}.{b^n}.\)
A.\(\frac{1}{{21}}.\)
B.\(\frac{1}{9}.\)
C.\(\frac{1}{{18}}.\)
D. \(\frac{1}{8}.\)
Cắt hình nón \(S\) bởi một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông cân có cạnh huyền bằng \(a\sqrt 2 .\) Tính theo \(a\) thể tích của khối nón đã cho.
A. \(\frac{{\pi {a^3}\sqrt 2 }}{4}.\)
B. \(\frac{{\pi {a^3}\sqrt 7 }}{3}.\)
C. \(\frac{{\pi {a^3}\sqrt 2 }}{{12}}.\)
D. \(\frac{{\pi {a^3}}}{4}.\)
Đồ thị hàm số \(y = - {x^4} + {x^2} + 2\) cắt trục \(Oy\) tại điểm nào?
A. \(A\left( {2;0} \right).\)
B. \(A\left( {0;0} \right).\)
C. \(A\left( {0; - 2} \right).\)
D. \(A\left( {0;2} \right).\)
Cho hình chữ nhật \(ABCD\) có \(AB = 5,BC = 4\). Tính thể tích của khối lăng trụ tạo thành khi cho hình chữ nhật \(ABCD\) quay quanh \(AB.\)
A. \(V = 100\pi .\)
B. \(V = 80\pi .\)
C. \(V = \frac{{80}}{3}\pi .\)
D. \(V = 20\pi .\)
Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong đó có đúng 2 học sinh nam?
A.6.
B.30.
C.24.
D. 12.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
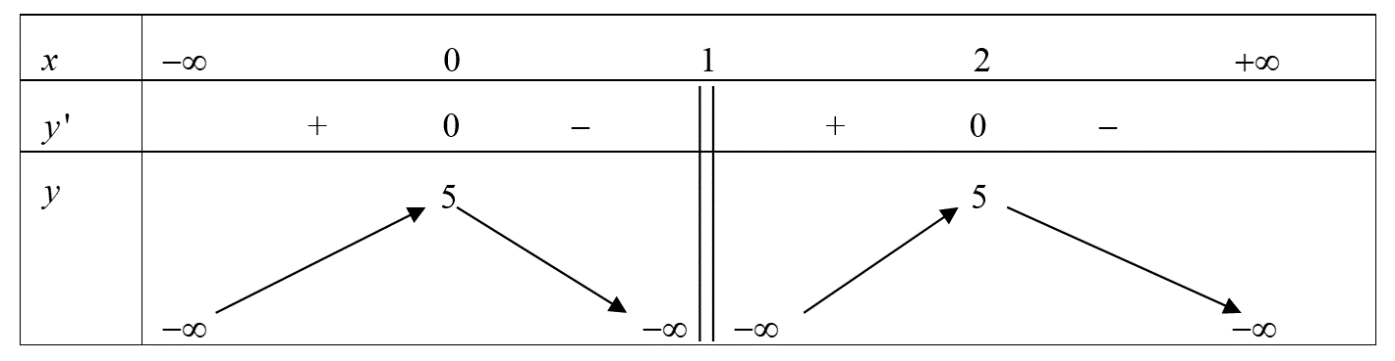
Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực tiểu
A.0.
B.3.
C.2.
D. 1.
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 2}},\) biết tiếp tuyến có hệ số góc \(k = - 3\)
A.\(y = - 3x + 4.\)
B.\(y = - 3x + 14\) và \(y = - 3x + 2.\)
C.\(y = - 3x - 14\) và \(y = - 3x - 2.\)
D.\(y = - 3x - 14.\)
Cho số thực dương \(a\) khác 1, biểu thức \(D = {\log _{{a^3}}}a\) có giá trị bằng bao nhiêu?
A. \( - \frac{1}{3}.\)
B. \(\frac{1}{3}.\)
C. \( - 3.\)
D. 3.
Tiếp tuyến của đồ thị hàm số \(y = \frac{{x + 1}}{{2x - 3}}\) tại điểm có hoành độ \({x_0} = - 1\) có hệ số góc bằng bao nhiêu?
A.5.
B.\(\frac{1}{5}.\)
C.\( - \frac{1}{5}.\)
D.\( - 5.\)
Tính đạo hàm của hàm số \(y = {\log _2}\left( {2x - 1} \right).\)
A.\(y' = \frac{2}{{2x - 1}}.\)
B.\(y' = \frac{1}{{\left( {2x - 1} \right)\ln 2}}.\)
C.\(y' = \frac{2}{{\left( {2x - 1} \right)\ln 2}}.\)
D.\(y' = \frac{1}{{2x - 1}}.\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 5\) và công bội \(q = - 2.\) Tìm số hạng thứ sáu của \(\left( {{u_n}} \right).\)
A. \({u_6} = - 160.\)
B.\({u_6} = - 320.\)
C.\({u_6} = 160.\)
D.\({u_6} = 320.\)
Hình nào dưới đây là hình đa diện?
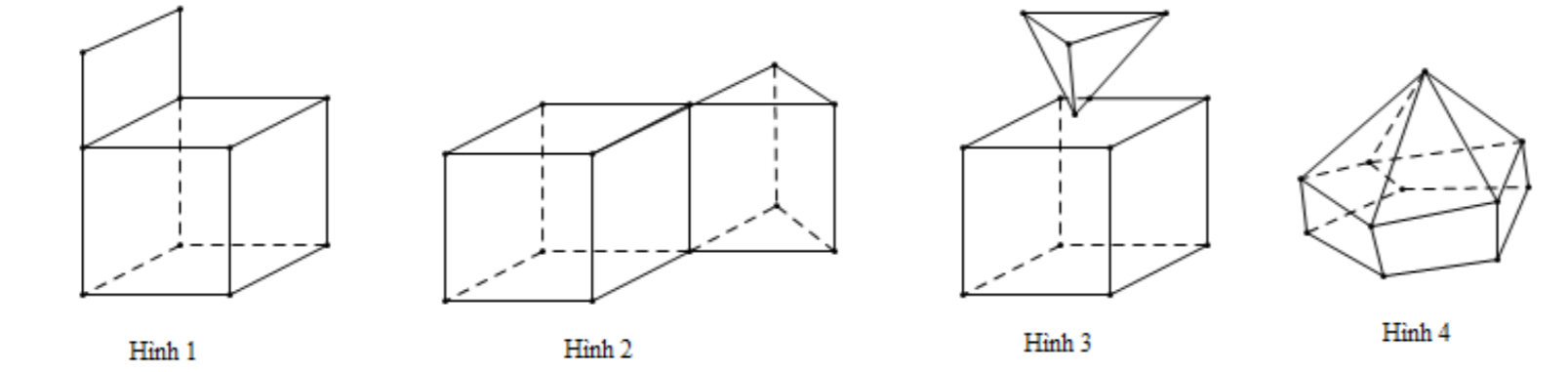
A.Hình 1.
B. Hình 4.
C.Hình 2.
D. Hình 3.
Cho hàm số \[y = f(x)\]có bảng biến thiên như sau:
![Cho hàm số \[y = f(x)\]có bảng biến thiên như sau:Đồ thị của hàm số đã cho có tổng số bao nhiêu tiệm cận đứng và tiệm cận ngang? (ảnh 1)](https://video.vietjack.com/upload2/images/1649615574/1649615751-image3.png)
Đồ thị của hàm số đã cho có tổng số bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.1.
B.3.
C.4.
D. 2.
Trong các hàm số sau, hàm số đồng biến trên \(\mathbb{R}?\)
A. \(y = \frac{{2x - 1}}{{x + 3}}.\)
B. \(y = {x^2} + 2x - 1.\)
C. \(y = 3x + 2.\)
D. \(y = {x^4} - 2{x^2}.\)
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích \(V.\) Tính thể tích của khối chóp tứ giác \(ABCC'B'.\)
A. \(\frac{1}{2}V.\)
B. \(\frac{1}{3}V.\)
C. \(\frac{2}{3}V.\)
D. \(\frac{3}{4}V.\)
Cho hình lăng trụ có bán kính đáy bằng 5. Biết rằng cắt hình trụ đã cho bởi một mặt phẳng qua trục của hình trụ, thiết diện thu được là một hình chữ nhật có chu vi bằng 32. Tính diện tích xung quanh của hình trụ đã cho.
A. \(110\pi .\)
B. \(55\pi .\)
C. \(60\pi .\)
D. \(150\pi .\)
Tính \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{2x - 1}}{{x + 1}}.\)
A. \( + \infty \)
B. \( - 1.\)
C. \( - 2.\)
D. \( - \infty .\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;4} \right]\) và có đồ thị như hình vẽ.
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;4} \right]\) và có đồ thị như hình vẽ.Phương trình \(3f\left( x \right) - 4 = 0\) có bao nhiêu nghiệm thực trên đoạn \(\ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/04/blobid0-1649620933.png)
Phương trình \(3f\left( x \right) - 4 = 0\) có bao nhiêu nghiệm thực trên đoạn \(\left[ { - 2;4} \right]?\)
A. 3.
B. 2.
C. 0.
D. 1.
Hàm số \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\) có tối đa bao nhiêu điểm cực trị?
A. 1.
B. 2.
C. 3.
D. 0.
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số \(y = \frac{{2 - x}}{{x + 3}}?\)
A. \(x = - 3.\)
B. \(y = - 1.\)
C.\(y = - 3.\)
D. \(x = 2.\)
Giải phương trình \({5^{2 - x}} = 125.\)
A. \(x = - 1.\)
B. \(x = - 5.\)
C. \(x = 3.\)
D. \(x = 1.\)
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\) là \(f'\left( x \right) = {x^2}\left( {x - 1} \right).\) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
A. \(\left( { - \infty ; + \infty } \right).\)
B.\(\left( {1; + \infty } \right).\)
C.
D.\(\left( {0;1} \right).\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
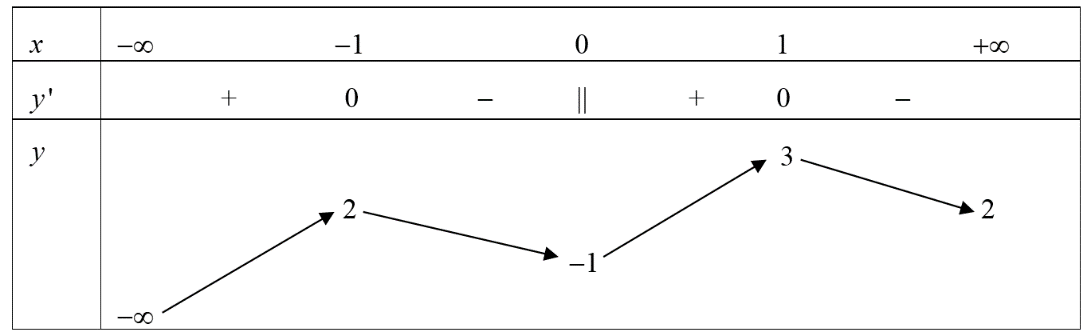
Mệnh đề nào sau đây đúng?
A.Hàm số đồng biến trên khoảng \(\left( { - 1;3} \right).\)
B.Hàm số nghịch biến trên khoảng \(\left( { - 2;1} \right).\)
C.Hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right).\)
D.Hàm số nghịch biến trên khoảng \(\left( {1;2} \right).\)
Tìm giá trị lớn nhất của hàm số \(y = {x^3} - 3{x^2}\) trên \(\left[ { - 1;2} \right].\)
A.-1.
B.0.
C.2.
D. \( - 4.\)
Tìm tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 3}}.\)
A.\(A\left( {3;2} \right).\)
B.\(B\left( { - 3;2} \right).\)
C.\(D\left( { - 1;3} \right).\)
D. \(C\left( {1; - 3} \right).\)
Đường cong ở hình vẽ sau là của hàm số nào dưới đây?
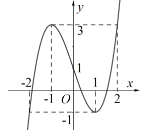
A.\(y = {x^3} - 3{x^2} + 1.\)
B.\(y = {x^4} - 2{x^2} + 1.\)
C.\(y = {x^3} - 3x + 1.\)
D.\(y = - {x^3} + 3x + 1.\)
Tính diện tích xung quanh \(Sxq\) của hình nón có bán kính đáy \(r = 3\) và độ dài đường sinh \(l = 5.\)
A.\({S_{xq}} = 30\pi .\)
B.\({S_{xq}} = 45\pi .\)
C.\({S_{xq}} = 24\pi .\)
D. \({S_{xq}} = 15\pi .\)
Tìm tập xác định của hàm số \(y = {\left( {x - 6} \right)^{ - 2019}}.\)
A.\(\left[ {6; + \infty } \right).\)
B.\(\mathbb{R}\backslash \left\{ 6 \right\}.\)
C.\(\mathbb{R}.\)
D. \(\left( {6; + \infty } \right).\)
Biết \({\log _7}2 = m,\) tính giá trị của \({\log _{49}}28\) theo \(m.\)
A.\(\frac{{m + 4}}{2}.\)
B.\(\frac{{1 + 4m}}{2}.\)
C.\(\frac{{1 + 2m}}{2}.\)
D. \(\frac{{1 + m}}{2}.\)
Cho hình nón đỉnh \(S,\) đường cao \(SO,A\) và \(B\) là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ \(O\) đến mặt phẳng \(\left( {SAB} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\) và \(\widehat {SAO} = {30^0},\widehat {SAB} = {60^0}.\) Tính độ dài đường sinh của hình nón theo \(a.\)
A.\(a\sqrt 3 .\)
B.\(2a\sqrt 3 .\)
C.\(a\sqrt 5 .\)
D. \(a\sqrt 2 .\)
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) vuông tại \(A,AB = a,BC = 2a,\) mặt bên \(ACC'A'\) là hình vuông. Gọi \(M,N,P\) lần lượt là trung điểm của \(AC,CC',A'B'\) và \(H\) là hình chiếu của \(A\) lên \(BC.\) Tính theo \(a\) khoảng cách giữa hai đường thẳng \(MP\) và \(HN.\)
A.\(\frac{{a\sqrt 3 }}{4}.\)
B.\(\frac{{a\sqrt 3 }}{2}.\)
C.\(a\sqrt 3 .\)
D. \(\frac{a}{4}.\)
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
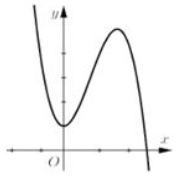
A.\(a >0,b < 0,c = 0,d >0\)
B. \(a >0,b < 0,c >0,d >0\)
C.\(a < 0,b >0,c >0,d >0\)
D.\(a < 0,b >0,c = 0,d >0\)
Đường thẳng \(y = {m^2}\) cắt đồ thị hàm số \(y = {x^4} - {x^2} - 10\) tại hai điểm phân biệt \(A,B\) sao cho tam giác \(OAB\) vuông (với \(O\) là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.\({m^2} \in \left( {5;7} \right).\)
B.\({m^2} \in \left( {3;5} \right).\)
C.\({m^2} \in \left( {0;1} \right).\)
D. \({m^2} \in \left( {1;3} \right).\)
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 20;2} \right]\) để hàm số đồng biến trên \(\mathbb{R}.\)
A. 2.
B.23.
C.20.
D. 3.
Phương trình \({3^x}{.5^{\frac{{2x - 1}}{x}}} = 15\) có một nghiệm dạng \(x = - {\log _a}b,\) với \(a,b\) là các số nguyên dương lớn hơn 1 và nhỏ hơn 8. Giá trị của biểu thức \(P = a + 2b\) bằng bao nhiêu?
A.\(P = 5.\)
B.\(P = 13.\)
C.\(P = 8.\)
D.\(P = 3.\)
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),\) hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\) vuông góc với nhau, \(SB = a\sqrt 3 ,\widehat {BSC} = {45^0},\widehat {ASB} = {30^0}.\) Thể tích khối chóp SABC là \(V.\) Tìm tỉ số \(\frac{{{a^3}}}{V}.\)
A.\(\frac{8}{3}.\)
B.\(\frac{{8\sqrt 3 }}{3}.\)
C.
D.\(\frac{{2\sqrt 3 }}{3}.\)
Cho biểu thức \(P = \frac{{{x^2} + xy + {y^2}}}{{x - xy + {y^2}}}\) với \({x^2} + {y^2} \ne 0.\) Tính giá trị nhỏ nhất của \(P.\)
A.\(\frac{1}{3}.\)
B.4.
C.1.
D.3
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - x - 2} \right)\left( {{x^3} - 6{x^2} + 11x - 6} \right).g\left( x \right)\) với \(g\left( x \right)\) là hàm đa thức có đồ thị như hình vẽ.
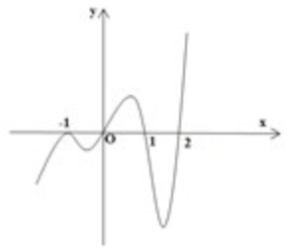
Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
A.5.
B.2.
C.3.
D.4.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định có bảng biến thiên như sau
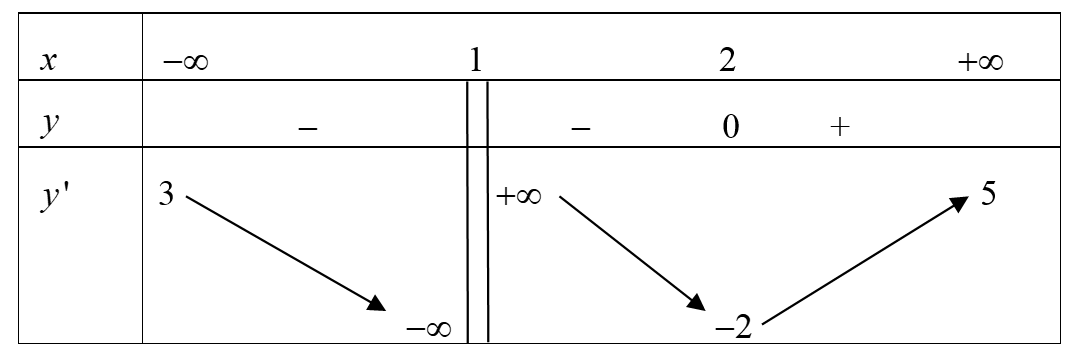
Đồ thị \(y = \frac{1}{{f\left( x \right) + 2}}\) có bao nhiêu đường tiệm cận đứng?
A. 3.
B. 1.
C. 2.
D. 4.
Cho lăng trụ đứng \(ABC.A'B'C'\) có độ dài cạnh bên là \(2a,\) đáy \(ABC\) là tam giác vuông cân tại \(A,\) góc giữa \(AC'\) và mặt phẳng \(\left( {BCC'B'} \right)\) bằng \({30^0}\) (tham khảo hình vẽ).
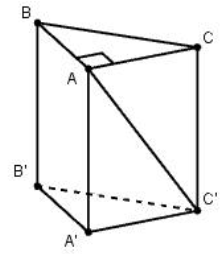
Tính theo \(a\) thể tích khối trụ có hai đáy là hai đường tròn ngoại tiếp hai đáy của lăng trụ \(ABC.A'B'C'.\)
A.\(\pi {a^3}.\)
B. \(3\pi {a^3}.\)
C.\(2\pi {a^3}.\)
D.\(4\pi {a^3}.\)
Cho hàm số \(y = {\left( {x + 2} \right)^{ - 2}}.\) Tìm hệ thức giữa \(y\) và không phụ thuộc vào \(x.\)
A.
B.
C.
D.
Cho hình hộp đứng có đáy là hình thoi cạnh Gọi \(G\) là trọng tâm của tam giác góc tạo bởi \(C'G\) và mặt đáy bằng \({30^0}.\) Tính theo \(a\) thể tích khối hộp
A.\({a^3}.\)
B. \(\frac{{{a^3}}}{3}.\)
C.\(\frac{{{a^3}}}{{12}}.\)
D.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ
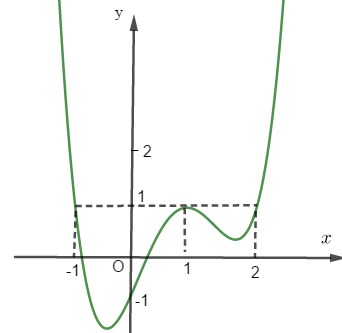
Hàm số \(g\left( x \right) = f\left( {x - 1} \right) + \frac{{2021 - 2020x}}{{2020}}\) đồng biến trên khoảng nào dưới đây?
A.\(\left( {0;1} \right).\)
B.(-1;0)
C.\(\left( {1;2} \right).\)
D. \(\left( {2;3} \right).\)
Tìm \(m\) để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - 4} \right)x + 3\) đạt cực đại tại điểm x=3.
A.\(m = - 1.\)
B. \(m = 1.\)
C.\(m = 5.\)
D. \(m = - 5.\)
Có bao nhiêu giá trị nguyên của \(m \in \left( { - 10;10} \right)\) để phương trình \(\frac{{\log \left( {mx + 1} \right)}}{{\log \left( {x + 1} \right)}} = 2\) có nghiệm thực duy nhất?
A. 15.
B. 10.
C. 16.
D. 11.
Cho hình chóp đều \(S.ABC\) có cạnh đáy bằng \(a,\) góc giữa mặt bên và mặt đáy bằng \({60^0}.\) Tính theo \(a\) diện tích xung quanh \({S_{xq}}\) của hình nón đỉnh \(S,\) có đáy là đường tròn ngoại tiếp \(\Delta ABC.\)
A. \({S_{xq}} = \frac{{\pi {a^2}\sqrt {10} }}{8}.\)
B.
C.\({S_{xq}} = \frac{{\pi {a^2}\sqrt 3 }}{3}.\)
D. \({S_{xq}} = \frac{{\pi {a^2}\sqrt 7 }}{4}.\)
Một lô hàng gồm 30 sản phẩm tốt và 10 sản phẩm xấu, lấy ngẫu nhiên đồng thời 3 sản phẩm. Tính sác xuất để trong 3 sản phẩm lấy ra có ít nhất 1 sản phẩm tốt.
A. \(\frac{{135}}{{998}}.\)
B.\(\frac{{15}}{{26}}.\)
C. \(\frac{3}{{247}}.\)
D. \(\frac{{244}}{{247}}.\)
Cho \({\log _a}x = 2;{\log _b}x = 3;{\log _c}x = 4,\left( {0 < a < b < c \ne 1,x >0} \right).\) Tính giá trị của biểu thức \({\log _{{a^2}b\sqrt c }}x.\)
A.\(\frac{{12}}{{13}}.\)
B.\(\frac{1}{9}.\)
C.\(\frac{6}{{13}}.\)
D. \(\frac{{24}}{{35}}.\)
Cho hàm số \(y = a{x^4} + b{x^3} + c{x^2} + dx + e\) với \(a,b,c,d,e\) là các số thực và \(a \ne 0,\) có bảng biến thiên như sau:
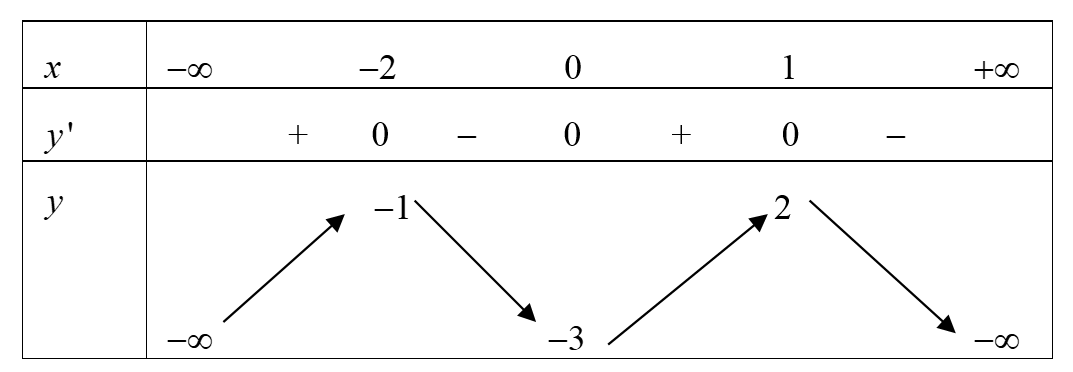
Đồ thị hàm số \(y = \frac{{{x^2}}}{{{f^2}\left( x \right) + 3f\left( x \right)}}\) có bao nhiêu tiệm cận đứng?
A. 4.
B. 3.
C. 5.
D. 6.


