50 CÂU HỎI
Hàm số nào dưới đây có tập xác định là khoảng ?
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho M(1;2;3), N(2;-3;1), P(3;1;2) . Tìm tọa độ điểm Q sao cho MNPQ là hình bình hành.
A.
B.
C.
D.
Công thức nào sau đây là sai
A.
B.
C.
D.
Tìm nghiệm của phương trình .
A. x=36
B. x=27
C. x=18
D. x=9
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng và cho mặt phẳng . Khẳng định nào dưới đây là khẳng định đúng?
A. d cắt
B.
C.
D.
Mặt phẳng nào dưới đây cắt mặt cầu theo thiết diện là một đường tròn?
A.
B.
C. Cả 3 đều sai.
D.
Giá trị cực tiểu của hàm số là
A.
B. -1
C.
D. 1
Thể tích của khối lập phương có cạnh bằng 2 là
A. 8
A. 8
C.
D. 6
Hàm số nghịch biến trên các khoảng nào dưới đây?
A. và
B.
C.
D.
Mệnh đề nào sau đây sai?
A.
B.
C.
D.
Cho số phức z=2-3i . Điểm biểu diễn số phức liên hợp của z là
A.
B.
C.
D.
Cho hình lập phương ABCD. A'B'C'D' ; cạnh bằng a . Gọi O là giao điểm của AC và BD . Thể tích của tứ diện OA'BC bằng
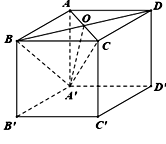
A.
B.
C.
D.
Trong không gian Oxyz cho điểm . Phương trình mặt phẳng (P) đi qua M cắt các trục tọa độ Ox, Oy, Oz; lần lượt tại A, B, C, sao cho M là trọng tâm của tam giácABC là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz. Phương trình mặt phẳng đi qua 3 điểm A(-3;0;0) , B(0;4;0) , C(0;0;-2) là
A.
B.
C.
D.
Biết rằng đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt A và B, biết điểm B có hoành độ âm. Hoành độ của điểm B bằng
A. -2
B. 0
C. -1
D. -5
Cho số thực x thỏa mãn (a, b, c là các số thực dương). Hãy biểu diễn x theo a, b, c.
A.
B.
C.
D.
Thể tích V của khối hộp chữ nhật biết là
A.
B.
C.
D.
Cho lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Thể tích của khối cầu đi qua các đỉnh của lăng trụ bằng
A.
B.
C.
D.
Số các đường tiệm cận đứng của đồ thị hàm số là
A. 3
B. 0
C. 1
D. 2
Sự tăng trưởng của một loài vi khuẩn tuân theo công thức trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng () và t là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu có 250 con và sau 12 giờ là 1500 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 216 lần số vi khuẩn ban đầu?
A. 66 giờ
B. 48 giờ
C. 36 giờ
D. 24 giờ
Cho tứ diện ABCD có , các tam giác ABC, ACD, ABD là các tam giác vuông tại đỉnh A. Khoảng cách d từ điểm A đến mặt phẳng là
A.
B.
C.
D.
Để đồ thị hàm số có điểm cực đại mà không có điểm cực tiểu thì tất cả các giá trị thực của tham số m là
A.
B.
C.
D.
Nếu thì giá trị của là
A. 12
B. 9
C. 12,5
D. 8
Cho số phức z thỏa mãn . Tính .
A. -1
B. i
C. -i
D. 1
Trong không gian hệ tọa độ Oxyz , cho điểm và mặt cầu (S) có phương trình . Tập các giá trị của a để điểm A nằm trong khối cầu là
A.
B.
C.
D.
Cho điểm và đường thẳng . Gọi d là đường thẳng đi qua M, cắt và vuông góc với Δ. Đường thẳng d có một véctơ chỉ phương là
A.
B.
C.
D.
Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị bằng
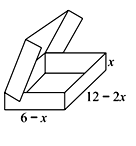
A. (đvdt)
B. (đvdt)
C. (đvdt)
D. (đvdt)
Phương trình mặt phẳng đi qua điểm và vuông góc với hai mặt phẳng , là
A.
B.
C.
D.
Bạn An cần mua một chiếc gương đường viền là Parabol bậc 2 (xem hình vẽ). Biết rằng khoảng cách đoạn AB=60cm, OH=30cm . Diện tích của chiếc gương bạn An mua là
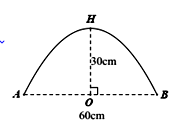
A.
B.
C.
D.
Trong mặt phẳng tọa độ Oxy, cho điểm M, N, P lần lượt là điểm biểu diễn của các số phức 2+3i. 1-2i, -3+i. Tọa độ điểm Q sao cho tứ giác MNPQ là hình bình hành là
A.
B.
C.
D.
Cho hàm số f(x) liên tục trên R thỏa mãn . Tích phân bằng
A. 16
B. 28
C. 36
C. 36
Đường thẳng x=k cắt đồ thị hàm số và đồ thị hàm số . Khoảng cách giữa các giao điểm là . Biết , trong đó a, b là các số nguyên. Khi đó tổng a+b bằng
A. 7
B. 6
C. 8
D. 5
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;1) . Mặt phẳng (P) thay đổi đi qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C khác gốc tọa độ. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC.
A. 18
B. 9
C. 6
D. 54
Cho hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự khác 0 và thỏa mãn đẳng thức . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ). Chọn phương án đúng và đầy đủ nhất.
A. Vuông cân tại O
B. Cân tại O.
C. Đều.
D. Vuông tại O.
Cho hình chóp S.ABCD có SA vuông góc với đáy; . Đáy ABCD là hình thang vuông tại A và B, . Gọi E là trung điểm AD. Tính bán
kính mặt cầu ngoại tiếp hình chóp S.ECD.
A.
B.
C.
D.
Với giá trị thực nào của tham số m thì đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt M, N sao cho MN ngắn nhất?
A.
B.
C.
D.
Cho số phức z thỏa mãn điều kiện . Trong mặt phẳng Oxy, tập hợp điểm biểu diễn số phức là hình tròn có diện tích bằng
A.
B.
C.
D.
Cho hàm số có đồ thị như hình bên. Tất cả các giá trị thực của tham số m thỏa mãn điều kiện để phương trình có đúng ba nghiệm phân biệt là
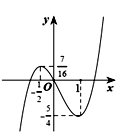
A. m=0 hoặc m=-6
B. m<0 hoặc m>6
C. 0<m<3
D. 1<m<6
Trong không gian Oxyz, cho . Phương trình mặt phẳng (P) sao cho nằm về hai phía (P) và (P) cách đều .
A.
B.
C.
D.
Trong không gian Oxyz, cho hai điểm A(-3;0;1), B(1;-1;3) và mặt phẳng (P): x-2y+2x-5=0 . Đường thẳng (d) đi qua A, song song với mặt phẳng (P) sao cho khoảng cách từ N đến đường thẳng d nhỏ nhất, đường thẳng (d) có một véctơ chỉ phương là u(1;b;c) , khi đó bằng
A.
B.
C.
D.
Cho hàm số với m là tham số thực. Tìm m để giá trị lớn nhất của hàm số trên đoạn đạt giá trị nhỏ nhất bằng .
A.
B.
C.
D. 6
Gọi S là tập các giá trị của tham số m để đường thẳng cắt đồ thị hàm số tại đúng một điểm. Tích phân các phần tử của S bằng.
A.
B. 4
C. 5
D. 20
Kết quả (b;c) của việc gieo một con súc sắc cân đối và đồng nhất hai lần liên tiếp, trong đó b là số chấm xuất hiện của lần gieo thứ nhất, c là số chấm xuất hiện của lần gieo thứ hai được thay vào phương trình bậc hai . Xác suất để phương trình bậc hai đó vô nghiệm là
A.
B.
C.
D.
Trên cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa hai cọc là 4 mét, còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung (lấy giá trị gần đúng nhất).
A.
B.
C.
D.
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình có đúng 6 nghiệm phân biệt thuộc đoạn là
![Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình f^2(cosx)+(m-2018)f(cosx)+m-2019=0 có đúng 6 nghiệm phân biệt thuộc đoạn [0; 2 pi] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/x-1655339013.png)
A. 1
B. 2
C. 3
D. 5
Cho hàm số (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số . Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng là
A.
B.
C.
D.
Một thùng rượu có bán kính đáy là thiết diện vuông góc với trục và cách đều hai đáy có bán kính là 40 cm, chiều cao thùng rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu (đơn vị lít) là bao nhiêu?

A. 425162 lít
B. 212581 lít
C. 212,6 lít
D. 425,2 lít
Trong không gian với hệ trục tọa độ Oxyz cho ba mặt phẳng ; . Một đường thẳng d thay đổi cắt ba mặt lần lượt tại ABC. Tìm giá trị nhỏ nhất của .
A. 24
B. 36
C. 72
D. 144
Cho khối chóp S.ABC có , . Gọi M, N lần lượt là các điểm trên cạnh AB và SC sao cho . Khi khoảng cách giữa M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN.
A.
B.
C.
D.
Cho hàm số f(x) có đạo hàm trên , biết với mọi . Giá trị của f(1) là
A.
B.
C.
D.


