50 CÂU HỎI
Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a. Hai mặt bên và cùng vuông góc với đáy và. Tính thể tích khối chóp S.ABC.
A.
B.
C.
D.
Cho hàm số thỏa mãn liên tục trên R và . Giá trị của f(3) là:
A. 6.
B. 3.
C. 10.
D. 9.
Cho a, b là các số dương tùy ý, khi đó ln(a+ab) bằng:
A.
B.
C.
D.
Họ nguyên hàm của hàm số là:
A.
B.
C.
D.
Bất phương trình có tập nghiệm là . Khi đó giá trị của là:
A. 4.
B. -4
C. 2.
D. -2
Trong hệ tọa độ Oxyz, cho đường thẳng . Phương trình nào sau đây là phương trình tham số của d?
A.
B.
C.
D.
Tìm số phức liên hợp của số phức .
A.
B.
C.
D.
Viết phương trình mặt phẳng (P) đi qua điểm A(0;-1;2) , song song với trục Ox và vuông góc với mặt phẳng (Q): x+2y-2z+1=0 .
A.
B.
C.
D.
Số phức z thỏa mãn z=5-8i có phần ảo là:
A. -8
B. 8.
C. 5.
D. -8i
Cho hàm số . Đồ thị hàm số có điểm cực đại là:
A.
B.
C.
D.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây:
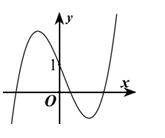
A.
B.
C.
D.
Cho hai mặt phẳng (P): 2x+2y+z+1=0, (Q): 2x-y+2z-1=0 và điểm A(1;2;3) . Phương trình đường thẳng d đi qua A song song với cả (P) và (Q) là:
A.
B.
C.
D.
Cho cấp số cộng có và . Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Trong hệ tọa độ Oxyz, cho hai điểm A(1;2;3), B( -1;4;1) . Phương trình mặt cầu đường kính AB là:
A.
B.
C.
D.
Số giao điểm của đường thẳng và đường cong là:
A. 1.
B. 0.
C. 3.
D. 2.
Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích của khối trụ là .
A.
B.
C.
D.
Phương trình có hai nghiệm là . Giá trị của là
A. 4.
B. 3.
C. 6.
D. 2.
Hàm số có đạo hàm với mọi x. Phát biểu nào sau đây đúng?
A. Hàm số có 1 điểm cực đại.
B. Hàm số không có điểm cực trị.
C. Hàm số có hai điểm cực trị.
D. Hàm số có đúng một điểm cực trị.
Giá trị của biểu thức bằng:
A. 2.
B. 4.
C. 3.
D. 16.
Tập xác định của hàm số là:
A.
B.
C.
D.
Cho hàm số . Tính tổng các giá trị của tham số m để .
A. -4
B. -2
C. -1
D. -3
Cho hình chóp S.ABCD có đáy là hình chữ nhật, , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SD và mặt phẳng đáy là . Diện tích mặt cầu ngoại tiếp hình chóp là:
A.
B.
C.
D.
Cho các đường thẳng và . Viết phương trình đường thẳng đi qua , cắt và vuông góc với .
A.
B.
C.
D.
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng , thể tích hình nón đã cho bằng:
A.
B.
C.
D.
Cho mặt phẳng (Q): z-y+2z-2=0 . Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q) , đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho
A.
B.
C.
D.
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a, góc giữa mặt phẳng và mặt phẳng bằng . Thể tích của khối lăng trụ ABC.A’B’C’ bằng:
A.
B.
C.
D.
Tích tất cả các nghiệm của phương trình là:
A. 1.
B.
C.
D.
Cho hàm số f(x) liên tục trên R và . Tính .
A. 30.
B. 10.
C. 20.
D. 5.
Cho hàm số . Với giá trị nào của m thì hai đường tiệm cận của đồ thị hàm số cùng với hai trục tọa độ tạo thành hình vuông.
A.
B.
C.
D.
Trong hệ trục tọa độ Oxyz, lập phương trình đường thẳng vuông góc chung của hai đường thẳng và
A.
B.
C.
D.
Có bao nhiêu số phức thỏa mãn ?
A. Vô số.
B. 2.
C. 1.
D. 0.
Biết với a, b là các số hữu tỉ. Giá trị của bằng:
A. 3.
B. 10.
C. 9.
D. 6.
Cho đường thẳng d: và điểm A(1;2;1) . Tìm bán kính của mặt cầu có tâm I nằm trên d, đi qua A và tiếp xúc với mặt phẳng (P): x-2y+2z+1=0 .đỉnh là đỉnh của đa giác đều đã cho?
A.
B.
C.
D.
Cho đa giác đều có 20 cạnh. Có bao nhiêu hình chữ nhật (không phải là hình vuông), có các đỉnh là đỉnh của đa giác đều đã cho?
A. 45.
B. 35.
C. 40.
D. 50.
Cho hàm số (với m là tham số). Có bao nhiêu giá trị của tham số m để các điểm cực trị của đồ thị hàm số đều nằm trên các trục tọa độ?
A. 2.
B. 0.
C. 3.
C. 3.
Cho hình trụ có trục OO’ và có bán kính đáy bằng 4: Một mặt phẳng song song với trục OO’ và cách OO’ một khoảng bằng 2 cắt hình trụ theo thiết diện là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng:
A.
B.
C.
D.
Cho đường thẳng . Viết phương trình mặt cầu tâm cắt d tại các điểm A, B sao cho .
A.
B.
C.
D.
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
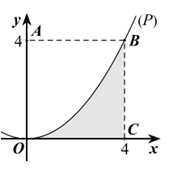
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân có . Cạnh bên SA vuông góc với đáy, . Gọi M là điểm nằm trên AC sao cho . Tính khoảng cách giữa SM và AB.
A.
B.
C.
D.
Phương trình có hai nghiệm là a và (với và là phân số tối giản). Giá trị của b là:
A. 1.
B. 4.
C. 2.
D. 3.
Cho hàm số liên tục và có đạo hàm trên , thỏa mãn hệ thức . Biết rằng trong đó . Tính giá trị của biểu thức .
A.
B.
C.
D.
Cho , đường thẳng và điểm M thuộc d. Tìm giá trị nhỏ nhất của diện tích tam giác AMB.
A.
B.
C.
D.
Cho phương trình . Tìm tất cả các giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thỏa mãn .
A. 4.
B. 5.
C. 3.
D. 6.
Cho hai số phức khác 0 thỏa mãn là số thuần ảo và . Giá trị lớn của bằng:
A. 10.
B.
C.
D. 20.
Cho hàm số liên tục trên R có đồ thị như hình vẽ. Biết trên thì . Số nghiệm nguyên thuộc của bất phương trình là:
>0 là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/s-1655424749.png)
A. 9.
B. 10.
C. 8.
D. 7.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAC) tạo với (SBC) một góc 60 độ và mặt phẳng (SAC) tạo với (SBC) một góc thỏa mãn . Gọi là góc tạo bởi SA và mặt phẳng (ABC) . Tính .
A.
B.
C.
D.
Cho hai hàm số với a khác 0 và có đồ thị như hình vẽ. Đồ thị hàm số đi qua gốc tọa độ và cắt đồ thị hàm số tại bốn điểm có hoành độ lần lượt là . Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ có hệ số góc bằng . Gọi (H) là hình phẳng giới hạn bởi hai đồ thị hàm số và (phần được tô đậm như hình vẽ). Diện tích của hình (H) bằng
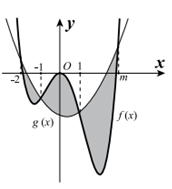
A.
B.
C.
D.
Cho hàm số liên tục trên R sao cho . Xét hàm số . Giá trị của tham số m để là
A. 5.
B. 4.
C. -1
D. 3.
Cho hàm số liên tục và xác định trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để bất phương trình có nghiệm với mọi x?
![Cho hàm số y=f(x) liên tục và xác định trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để bất phương trình 3. 13^f(x)+[f^2(x)-10].16^f(x)>= (m^2+3m).3^2f(x) có nghiệm với mọi x? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/c-1655425981.png)
A. 5.
B. 7.
C. Vô số.
D. 6.
Cho hàm số với m là tham số thực. Biết rằng hàm số có số điểm cực trị lớn hơn 5 khi . Giá trị bằng:
A. 8.
B. 6.
C. 7
D. 5.


