50 CÂU HỎI
Hàm số nào sau đây có đồ thị như hình vẽ bên dưới?
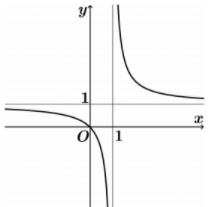
A.
B.
C.
D.
Tìm tất cả các điểm M nằm trên đồ thị hàm số mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng .
A.
B. hoặc \[M\left( { - 2;4} \right)\]
C.
D.
Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\] và điểm . Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.
A. và .
B. và .
C. và .
D. và .
Mệnh đề nào dưới đây về hàm số là đúng?
A. Nghịch biến trên
B. Đồng biến trên
C. Đồng biến trên và\[\left( {2; + \infty } \right)\]
D. Đồng biến trên và \[\left( {2; + \infty } \right)\].
Cho một hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tính thể tích khối càu nội tiếp trong hình nón.
A.
B.
C.
D.
Một người gửi tiền vào ngân hàng với lãi suát không đổi là 6% trên năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (lãi kép). Người đó định gửi tiền trong vòng 3 năm, sau đó rút ra 500 triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng (làm tròn đến hàng triệu) là bao nhiêu triệu đồng?
A.420.
B.410.
C.400.
D. 390.
Cho biết và . Tính theo a và b.
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên đoạn bằng:
A.
B.
C.-1
D.
Hàm số \[y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\] nhận giá trị nhỏ nhất trên đoạn tại:
A.
B.
C.
D.
Sau đây, có bao nhiêu hàm số mà đồ thị có đúng một tiệm cận ngang?
1) \[y = \frac{{\sin x}}{x}\] 2)
3) 4)
A.1
B.2
C.3
D.4
Cho tứ diện ABCD có ABC và ABD là các tam giác đều cạnh a, ACD và BCD là các tam giác vuông tương ứng tại A và B. Tính thể tích khối tứ diện ABCD.
A.
B.
C.
D.
Giá trị lớn nhất của hàm số trên đoạn bằng:
A.
B.
C.
D.
Hàm số \[y = \left( {x + 1} \right)\left( {x - 2} \right)\left( {3 - x} \right)\] có số điểm cực trị là:
A. 2
B. 3
C. 0
D. 1
bằng:
A.
B.\[\ln \left| {\cos x} \right| + C\]
C.
D.
Kết luận nào sau đây đúng về hàm số ?
A.
B. nghịch biến trên
C. \[f\left( 0 \right) = 0\]
D. đồ thị nhận trục tung làm tiệm cận ngang.
Một nguyên hàm của hàm số là bằng:
A.
B.
C.
D.
Kết luận nào sau đây và hàm số là sai?
A. Đồ thị có tiệm cận đứng là đường thẳng có phương trình .
B. Đồng biến trên khoảng .
C.
D.
Trong các hàm số sau đây có bao nhiêu hàm số có đúng một điểm cực trị?
1) 2)
3) \[y = \left( {2x - 1} \right)\sqrt[3]{{{x^2}}}\] 4)
A. 0
B. 1
C. 3
D. 2
Cho hình chóp S.ABC, đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt đáy. Biết SA = AB = BC và diện tích mặt cầu ngoại tiếp hình chóp bằng . Thể tích khối chóp là:
A.
B.
C.
D.
Hàm số nào sau đây mà đồ thị có dạng như hình vẽ bên dưới?
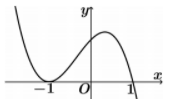
A.\[y = \left( {x + 1} \right){\left( {x - 1} \right)^2}\]
B.
C.
D.
Hàm số nào sau đây mà đồ thị có dạng như hình vẽ bên dưới?
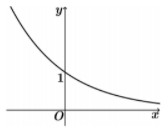
A.
B.
C.
D.
Cho một hình nón đỉnh S đáy là đường tròn (O), bán kính đáy bằng 1. Biết thiết diện qua trục là một tam giác vuông. Tính diện tích xung quanh của hình nón.
A.
B.
C.
D.
Cho hàm số có đạo hàm thỏa mãn . Khi đó bằng:
A. 4
B. 1
C. 2
D. 3
Cho hình lăng trụ đứng ABC.A’B’C’. Đáy là tam giác vuông tại A, có BC = 2AC = 2a. Đường thẳng AC’ tạo với mặt phẳng (BCC’B’) một góc . Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng;
A.
B.
C.
D.
Số tiệm cận của đồ thị hàm số là:
A. 3
B. 1
C. 4
D. 2
Một nguyên hàm của bằng:
A.\[x - x\ln x\]
B.
C.
D.
Cho hàm số có đạo hàm . Hỏi hàm số đồng biến trên khoảng nào sau đây?
A.\[\left( { - \infty ;1} \right)\] và
B. và
C.\[\left( {1;2} \right)\]
D.
Qua điểm M(2;0) kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số ?
A. 1
B. 2
C. 3
D. 4
Tập xác định của hàm số là:
A.
B.
C.
D.
Cho một hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng a. Gọi AB và CD là hai đường kính tương ứng của hai đáy. Biết góc giữa hai đường thẳng AB và CD bằng . Tính thể tích khối tứ diện ABCD.
A.
B.
C.\[\frac{{{a^3}}}{6}\]
D.
Cho các số nguyên a, b, c thỏa mãn . Tổng bằng:
A. 1
B. 4
C. 2
D. 0
Cho hàm số có đạo hàm liên tục trên , thỏa mãn . Biết , tính f.
A. 16
B. 2
C. 8
D. 4
Cho hàm số có đạo hàm \[f'\left( x \right) = - \frac{x}{{{x^2} + 1}}\]. Với a và b là các số dương thỏa mãn , giá trị nhỏ nhất của hàm số trên đoạn bằng:
A.\[f\left( b \right)\]
B.
C.
D.
Cho một hình trụ thay đổi nội tiếp trong một hình nón cố định cho trước (tham khảo hình vẽ bên). Gọi thể tích các khối nón và khối trụ tương ứng là V và V’. Biết rằng V’ là giá trị lớn nhất đạt được, khi đó tỉ số \[\frac{{V'}}{V}\] bằng:
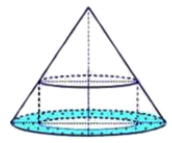
A.
B.
C. \[\frac{1}{2}\]
D.
Cho hàm số liên tục trên , có bảng biến thiên như hình vẽ dưới đây:
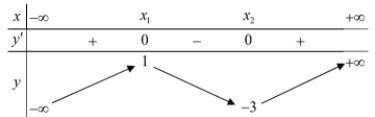
Đặt (m là tham số). Tìm tất cả các giá trị của m để hàm số có đúng 3 điểm cực trị.
A. hoặc
B.
C. hoặc
D.
Cho phương trình , m là tham số. Hỏi có bao nhiêu giá trị nguyên dương của m để phương trình có nghiệm?
A. 5
B. 4
C. 6
D. 7
Trong không gian tọa độ , cho điểm . Hình chiếu của M tương ứng lên là . Gọi P và Q tương ứng là giao điểm của đường thẳng OM với các mặt phẳng và . Độ dài PQ bằng:
A.
B. \[\frac{7}{6}\]
C.
D.
Giả sử . Giá trị của tổng bằng:
A. 1
B.
C.-1
D. 4
Tìm số nghiệm của phương trình trên đoạn .
A. 672
B. 643
C. 642
D. 673
Cho hàm số f(x) xác định trên , thỏa mãn và . Giả sử phương trình có hai nghiệm và . Tính tổng .
A. 5
B. 999
C. 3
D. 1001
Cho hình lăng trụ đều ABC.A’B’C’, tất cả các cạnh có độ dài bằng a. Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM và BC’.
A.
B.
C.
D.
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Mặt phẳng đi qua A và vuông góc với A’C chia hình lập phương trình hai phần thể tích. Tính tỉ số k hai phần thể tích này, biết  .
.
A.
B.
C.
D.
Chọn ngẫu nhiên 4 đỉnh của một đa giác lồi (H) có 30 đỉnh. Tính xác suất sao cho 4 đỉnh được chọn tạo thành một tứ giác có bốn cạnh đều là đường chéo của (H).
A.
B.
C.
D.
Cho một hình hộp đứng ABCD.A’B’C’D’. Đáy ABCD là hình thoi cạnh bằng a và \[\angle BAD = {60^0}\]. Một mặt phẳng tạo với đáy một góc và cắt tất cả các cạnh bên của hình hộp. Tính diện tích thiết diện tạo thành
A.
B.
C.
D.
Cho tứ diện ABCD có ABC và ABD là các tam giác đều cạnh bằng a không đổi. Độ dài CD thay đổi. Tính giá trị lớn nhất đạt được của thể tích khối tứ diện ABCD.
A.
B.
C.
D.
Cho tứ diện ABCD có ABC, ABD, ACD là các tam giác vuông tương ứng tại A, B, C. Góc giữa AD và (ABC) bằng , và khoảng cách giữa AD và BC bằng a. Tính thể tích khối tứ diện ABCD.
A.
B.
C.
D.
Cho hàm số có đạo hàm . Tìm số điểm cực trị của hàm số .
A. 1
B. 2
C. 3
D. 5
Cho tứ diện ABCD có AC = AD = BC = BD = a. Các cặp mặt phẳng (ACD) và (BCD), (ABC) và (ABD) vuông góc với nhau. Tính theo a độ dài cạnh CD.
A.
B.
C.
D.
Cho hàm số . Tìm m để mọi bộ ba số phân biệt a, b, c thuộc đoạn thì là độ dài ba cạnh của một tam giác.
A.
B.
C.
D.
Cho hình hộp ABCD.A’B’C’D’ có đáy là hình thoi cạnh a và . Mặt chéo ACC’A’ nằm trong mặt phẳng vuông góc với đáy, đồng thời ACC’A’ cũng là hình thoi có . Thể tích khối tứ diện ACB’D’ là:
A.
B.
C.
D.


