Quiz

Đề thi cuối kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới có đáp án (Đề 3)

Admin13 câu hỏiToánLớp 12

Bắt đầu ngay

13 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hàm số y = f(x) có đồ thị là đường cong hình bên

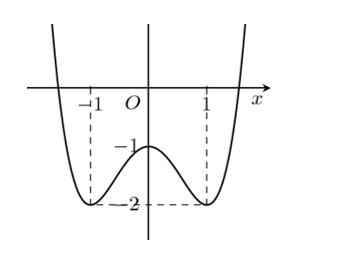
Cho hàm số y = f(x) có đồ thị là đường cong hình bên Hàm số đã cho nghịch biến trên khoảng nào dưới đây? (ảnh 1)

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $(1; + \infty)$ .

B. $(0; 1)$ .

C. $(- 1; 0)$ .

D. $(- \infty; 0)$ .

2. Nhiều lựa chọn

Cho hàm số $y = f (x)$ liên tục trên đoạn $[- 1; 2]$ và có đồ thị như hình vẽ sau

Cho hàm số y = f(x) liên tục trên đoạn [-1;2] và có đồ thị như hình vẽ sau Giá trị lớn nhất của hàm số y = f(x) trên đoạn [1;2] là (ảnh 1)

Giá trị lớn nhất của hàm số $y = f (x)$ trên đoạn $[- 1; 2]$ là

A. 3.

B. $- 1$ .

C. 1.

D. 2

3. Nhiều lựa chọn

Hàm số $y = \log_{5} (10 x - x^{2})$ đồng biến trên khoảng nào trong các khoảng dưới đây?

A. $(5; 10)$ .

B. $(0; 10)$ .

C. $(0; 10)$ .

D. $(10; + \infty)$ .

4. Nhiều lựa chọn

Gọi m và M lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f (x) = e^{2 - 3 x}$ trên đoạn $[0; 2] .$ Mối liên hệ giữa M và m là

A. $M - m = e$ .

B. $m + M = 1$ .

C. $m . M = \frac{1}{e^{2}}$ .

D. $\frac{M}{m} = e^{2}$ .

5. Nhiều lựa chọn

Cho hình hộp ABCD.A'B'C'D'. Vectơ $\vec{u} = \vec{B B^{'}} + \vec{B A} + \vec{B C}$ bằng vectơ nào dưới đây?

A. $\vec{B D}$ .

B. $\vec{B D'}$ .

C. $\vec{B C}$ .

D. $\vec{B A'}$

6. Nhiều lựa chọn

Trong không gian Oxyz, biết $\vec{O M} = 2 \vec{i} - 3 \vec{j} + \vec{k}$ . Toạ độ của điểm M là

A. $(- 2; 3; - 1)$ .

B. $(2; - 3; 1)$ .

C. $(- 3; 2; 1)$ .

D. $(2; 1; - 3)$ .

7. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (- 2; 1; 0)$ , $B (0; - 2; 5)$ , $C (6; - 2; 1)$ . Tích vô hướng của hai vectơ $\vec{A B}$ và $\vec{B C}$ là

A. $\sqrt{38} . \sqrt{52}$ .

B. $- \sqrt{38} . \sqrt{52}$ .

C. 8.

D. - 8.

8. Nhiều lựa chọn

Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{E G}$ ?

A. $60 °$ .

B. $45 °$ .

C. $90 °$ .

D. $120 °$ .

9. Nhiều lựa chọn

Cho hàm số $y = f(x)$ có đồ thị là đường cong hình bên

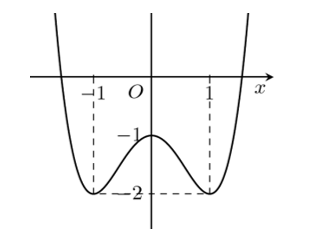
Cho hàm số (y = f(x)) có đồ thị là đường cong hình bên (ảnh 1)

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.$(1; + \infty )$.

B.$(0;1)$.

C.$( - 1;0)$.

D.$( - \infty ;0)$.

10. Nhiều lựa chọn

Cho hai điểm $M\left( {0\,;\,0\,;\,2} \right)$ và $N\left( {4\,;\, - 2;\,6} \right)$. Tìm tọa độ điểm $P$ sao cho $N$ là trung điểm của $MP$?

A. $P\left( {2\,;\, - 1\,;\,4} \right)$.

B. $\left( {4\,;\, - 2\,;\,4} \right)$.

C. $\left( {2\,;\, - 1\,;\,2} \right)$.

D. $P\left( {8\,;\, - 4\,;\,10} \right)$.

11. Nhiều lựa chọn

Trong không gian với hệ tọa độ $Oxyz$, cho hai vectơ $\overrightarrow u = \left( {3; - 1;1} \right)$ và $\overrightarrow v = \left( {1;2; - 2} \right)$. Độ dài của vectơ $\overrightarrow u + \overrightarrow v $ là

A. $\sqrt {10} $.

B. $\sqrt {11} + 3$.

C. $3\sqrt 2 $.

D. $5$.

12. Nhiều lựa chọn

Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được thống kê ở bảng sau:

Thời gian sử dụng	$\left[ {7,2;7,4} \right)$	$\left[ {7,4;7,6} \right)$	$\left[ {7,6;7,8} \right)$	$\left[ {7,8;8,0} \right)$
Số máy	2	4	7	6

Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

A.$0,192$.

B. $0,197$.

C. $0,037$.

D. $0,2$.

13. Nhiều lựa chọn

Bốn bạn Ánh, Ba, Châu, Dũng cùng là thành viên của một câu lạc bộ rubik. Trong một lần luyện tập rubik với nhau, mỗi bạn đã cùng giải rubik 30 lần liên tiếp và thống kê kết quả lại ở bảng sau:

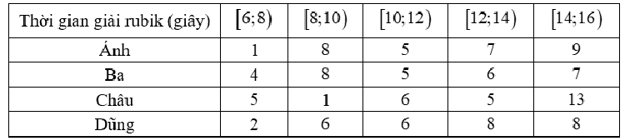
Bốn bạn Ánh, Ba, Châu, Dũng cùng là thành viên của một câu lạc bộ rubik. Trong một lần luyện tập rubik với (ảnh 1)

Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì bạn nào có tốc độ giải rubik đồng đều nhất?

A. Ánh.

B. Ba.

C. Châu.

D. Dũng.

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube

Thời gian sử dụng	\(\left[ {7,2;7,4} \right)\)	\(\left[ {7,4;7,6} \right)\)	\(\left[ {7,6;7,8} \right)\)	\(\left[ {7,8;8,0} \right)\)
Số máy	2	4	7	6