12 CÂU HỎI
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
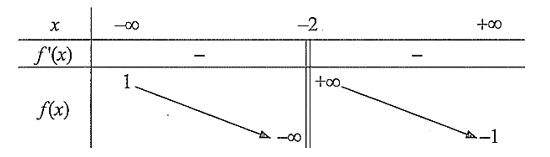
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. \(1\).
B. \(2\).
C. \(3\).
D. \(4\).
Cho hàm số \(y = {e^x}\left( {x - 2} \right)\). Hàm số nghịch biến trên khoảng nào sau đây?
A. \(\left( {2; + \infty } \right)\).
B. \(\left( {1; + \infty } \right)\).
C. \(\left( { - \infty ;2} \right)\).
D. \(\left( { - \infty ;1} \right)\).
Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = x + 1 - \frac{4}{{x - 3}}\) trên đoạn \(\left[ { - 1;2} \right]\). Giá trị của \(M - m\) bằng
A. \(1\).
B. \(\frac{9}{5}\).
C. \(6\).
D. \(8\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{2x + 1}}{{x - m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 4} \right)\)?
A. \(3\).
B. \(4\).
C. \(5\).
D.Vô số.
Hàm số nào sau đây là một nguyên hàm của hàm số \(f\left( x \right) = \sin x\)?
A. \({F_1}\left( x \right) = \sin x\).
B. \({F_2}\left( x \right) = - \sin x\).
C. \({F_3}\left( x \right) = \cos x\).
D.\({F_4}\left( x \right) = - \cos x\).
Biết rằng \(\int\limits_0^1 {\frac{{2{e^{2x}} + 3}}{{{e^x}}}} \,{\rm{d}}x = \frac{{m \cdot {e^2} + n \cdot e + p}}{e}\) (với \(m,n,p \in \mathbb{Z}\)). Khi đó \(m + 2n - p\) bằng
A. \(2\).
B. \(6\).
C. \(1\).
D.\(7\).
Cho \(A\) và \(B\) là hai biến cố độc lập thoả mãn \(P\left( A \right) = 0,5\) và \(P\left( B \right) = 0,3\). Khi đó, \(P\left( {A \cap B} \right)\) bằng:
A. \(0,8\).
B. \(0,2\).
C. \(0,6\).
D. \(0,15\).
Bảng sau ghi lại điểm tổng kết cuối năm môn Ngữ văn của các học sinh lớp 12D.
|
Điểm |
\[\left[ {7;\,7,5} \right)\] |
\[\left[ {7,5;\,8} \right)\] |
\[\left[ {8;\,8,5} \right)\] |
\[\left[ {8,5;\,9} \right)\] |
|
Số học sinh |
6 |
16 |
13 |
5 |
Phương sai của mẫu số liệu trên thuộc khoảng
A. \(\left[ {0;0,2} \right)\).
B. \(\left[ {2,0;2,2} \right)\).
C. \(\left[ {3,3;3,5} \right)\).
D. \(\left[ {3,5;3,7} \right)\).
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(BC,CD\) và \(G\) là trọng tâm của tam giác \(BCD\). Phát biểu nào sau đây sai?
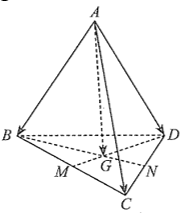
A. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).
C. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AN} = 3\overrightarrow {AG} \).
D. \(\overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AN} \).
Trong không gian \(Oxyz\), cho mặt cầu tâm \(I\left( { - 2;1;5} \right)\), bán kính bằng \(3\). Điểm nào dưới đây thuộc mặt cầu đã cho?
A. \(C\left( {0;3;4} \right)\).
B. \(A\left( {10;1;2} \right)\).
C. \(B\left( {0;1;4} \right)\).
D. \(D\left( {0;2;1} \right)\).
Trong không gian \(Oxyz\), góc giữa hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + t\\z = - 1 + t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 3 - t\\y = 1 - 2t\\z = 5 + t\end{array} \right.\) bằng
A. \(60^\circ \).
B. \(120^\circ \).
C. \(30^\circ \).
D. \(90^\circ \).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_2} = - 6\) và \({u_6} = - 486\). Tìm công bội \(q\) của cấp số nhân đã cho, biết rằng \({u_3} > 0\).
A. \(q = - 3\).
B. \(q = - \frac{1}{3}\).
C. \(q = \frac{1}{3}\).
D. \(q = 3\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
