12 CÂU HỎI
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
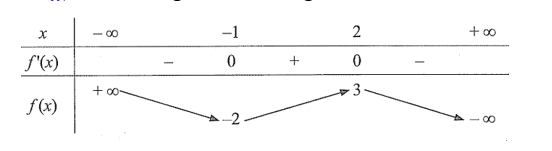
Giá trị cực đại của hàm số đã cho là
A. \(3\).
B. \( - 2\).
C. \( - 1\).
D. \(2\).
Có bao nhiêu số nguyên \(a\) sao cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + 3x + 1\) đồng biến trên \(\mathbb{R}\)?
A. \(0\).
B. \(3\).
C. \(6\).
D. \(7\).
Trong không gian tọa độ \(Oxyz,\)vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( P \right):2x - y + z + 3 = 0\)?
A. \(\overrightarrow {{n_1}} = \left( {2\,;\, - 1\,;\,\,1} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {2\,;\,1\,;\,1} \right)\).
C. \(\overrightarrow {{n_3}} = \left( {2\,;\, - 1\,;\,3} \right)\).
D. \(\overrightarrow {{n_4}} = \left( { - 1\,;\,1\,;\,3} \right)\).
Số tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} + x - 2}}{{{x^2} - 4}}\) là
A. \(0\).
B. \(1\).
C. \(2\).
D. \(3\).
Biết hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = {4^x}\) và \(F\left( 1 \right) = \frac{1}{{\ln 2}}\). Giá trị của \(F\left( {\frac{3}{2}} \right) \cdot \ln 2\) bằng
A. \(3\).
B. \(7\).
C. \(5\).
D. \(9\).
Diện tích hình phẳng giới hạn bởi parabol \(\left( P \right):y = f\left( x \right) = {x^2} - 1\), trục tung và tiếp tuyến của \(\left( P \right)\) tại điểm \(M\left( { - 1;0} \right)\) bằng
A. \(\frac{5}{3}\).
B. \(\frac{2}{3}\).
C. \(\frac{1}{3}\).
D. \(\frac{4}{3}\).
Bất phương trình \({\log _3}\left( {{x^2} - x + 7} \right) < 2\) có tập nghiệm là khoảng \(\left( {a;b} \right)\). Tính \(b - a\).
A. \(b - a = - 1\).
B. \(b - a = - 3\).
C. \(b - a = 3\).
D. \(b - a = 1\).
Cho hai biến có \(A\) và \(B\) có \(P\left( A \right) = 0,7;P\left( B \right) = 0,5\) và \(P\left( {A \cup B} \right) = 0,8\). Xác suất của biến cố \(A\) với điều kiện \(B\) là
A. \(0,4\).
B. \(0,5\).
C. \(0,7\).
D. \(0,8\).
Trong không gian tọa độ \(Oxyz\), mặt cầu \(\left( S \right)\) có tâm \(I\left( {2;1; - 1} \right)\) và đường kính 6 có phương trình là
A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 36\).
B. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 9\).
C. \({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 9\).
D. \({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 36\).
Dùng đồ thị hàm số \(y = - \sin x\) (tham khảo hình vẽ), xác định số nghiệm của phương trình \(2\sin x + \sqrt 2 = 0\) trên đoạn \( - \frac{{3\pi }}{2} \le x \le \frac{{3\pi }}{2}\).
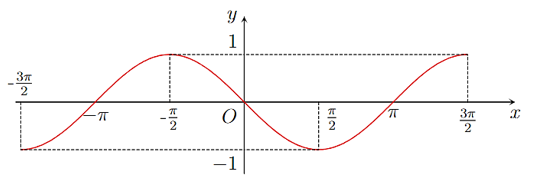
A. \(2\).
B. \(3\).
C. \(1\).
D. \(4\).
Thời gian thực hiện xong một thí nghiệm hóa học của học sinh lớp 12H được ghi lại ở bảng sau:
|
Thời gian (phút) |
\(\left[ {5;\,6} \right)\) |
\(\left[ {6;\,7} \right)\) |
\(\left[ {7;\,8} \right)\) |
\(\left[ {8;\,9} \right)\) |
\(\left[ {9;\,10} \right)\) |
|
Số học sinh |
12 |
25 |
0 |
0 |
1 |
Khoảng biến thiên của mẫu số liệu trên là
A. \(5\).
B. \(4\).
C. \(2\).
D. \(1\).
Trong không gian \(Oxyz\), đường thẳng đi qua hai điểm \(A\left( { - 1;1;0} \right)\) và \(B\left( {3;2; - 1} \right)\) có phương trình tham số là
A. \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 + t\\z = t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = - 1 + 4t\\y = 1 + t\\z = - t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 + t\\z = - t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = - 1 + 4t\\y = 1 + t\\z = t\end{array} \right.\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải