32 CÂU HỎI
I. PHẦN TRẮC NGHIỆM (4,0 điểm) – 50 phút
Căn bậc hai số học của 9 là
A. 3.
B. \( - 3\).
C. \(3;\,\, - 3.\)
D. 81.
Biểu thức \(\sqrt[3]{{x - 1}}\) có điều kiện xác định là
A. \(x \ge 1\).
B. \(x \in \mathbb{R}\).
C. \(x \ne 1\).
D. \(x > 1\).
Cho \(a,\,\,b,\,\,c\) là các số thực thỏa mãn \(a + b + c - 21 = 2\left( {\sqrt {a - 7} + \sqrt {b - 8} + \sqrt {c - 9} } \right)\). Giá trị của biểu thức \(S = a + 2b - c\) là
A. \(S = 36\).
B. \(S = 16\).
C. \(S = 7\).
D. \(S = 14\).
Điểm nào sau đây thuộc đồ thị hàm số \(y = 2{x^2}\)?
A. \(\left( {2;1} \right)\).
B. \(\left( {1;2} \right)\).
C. \(\left( {1;4} \right)\).
D. \(\left( {4;1} \right)\).
Biết rằng đường cong trong hình bên là một parabol \(y = a{x^2}.\) Quan sát hình vẽ và cho biết parabol trong hình vẽ bên đi qua điểm nào dưới đây?
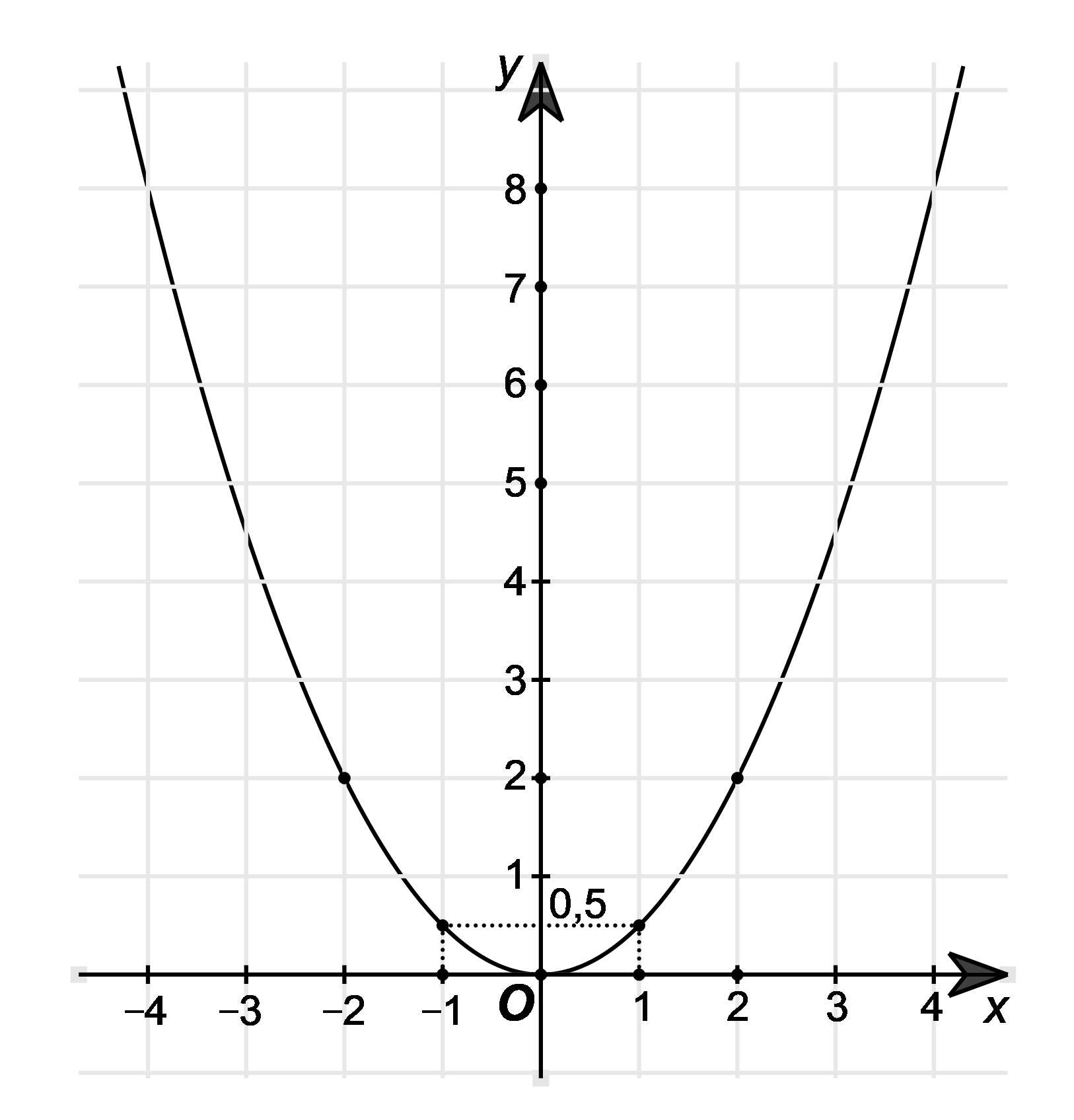
A. \(\left( { - 1;1} \right)\).
B. \(\left( {2; - 2} \right)\).
C. \(\left( {0,5;1} \right)\).
D. \(\left( {2;2} \right)\).
Giao điểm của parabol \(y = {x^2}\) và đường thẳng \(y = x + 2\) cùng với gốc tọa độ tạo thành tam giác có diện tích bằng
A. 4.
B. 7.
C. 6.
D. 3.
Giải phương trình \(\left( {x + \frac{1}{3}} \right)\left( {x - 3} \right) = 0\) ta được các nghiệm là
A. \(x = - \frac{1}{3}\).
B. \(x = 3\).
C. \(x = - \frac{1}{3}\) và \(x = 3\).
D. \(x = \frac{1}{3}\) và \(x = - 3\).
Bất phương trình nào dưới đây là bất phương trình bậc nhất một ẩn?
A. \(0x + 3 > 0\).
B. \(2x + 1 < 0\).
C. \(2{x^2} + 1 \le 0\).
D. \(\frac{1}{{3x - 5}} \le 0\).
Trong các phương trình bậc hai sau phương trình nào có tổng hai nghiệm bằng 3?
A. \({x^2} - 3x + 3 = 0\).
B. \(2{x^2} - 6x + 3 = 0\).
C. \({x^2} - 3x + 6 = 0\).
D. \({x^2} - 6x + 3 = 0\).
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = - 1}\\{2x - y = 4}\end{array}} \right.\) có nghiệm là \(\left( {{x_0};{y_0}} \right).\) Giá trị của biểu thức \(2{x_0} + {y_0}\) bằng
A. \[ - 3.\]
B. \[ - 1.\]
C. 0.
D. 3.
Bắc có số tiền không vượt quá 60 000 đồng gồm 15 tờ với hai loại mệnh giá 2 000 đồng và 5 000 đồng. Hỏi Bắc có nhiều nhất bao nhiêu tờ tiền mệnh giá 5 000 đồng?
A. 7 tờ.
B. 8 tờ.
C. 9 tờ.
D. 10 tờ.
Điều kiện xác định của phương trình \(\frac{{2x + 1}}{{x - 2}} = \frac{1}{3}\) là
A. \(x \ne 2\).
B. \(x \ne - 2\).
C. \(x \ne 0\).
D. \(x = 2\).
Bạn Bắc gieo một con xúc xắc 50 lần cho kết quả như sau:
|
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
|
Tần số |
8 |
7 |
10 |
8 |
6 |
11 |
Tần số xuất hiện mặt 3 chấm là
A. 9.
B. 10.
C. 11.
D. 12.
Đo chiều cao (đơn vị cm) của học sinh lớp 9A ở một trường THCS người ta thu được bảng tần số ghép nhóm như sau:
|
Chiều cao \(({\rm{cm}})\) |
\(\left[ {150;\,\,158} \right)\) |
\(\left[ {158;\,\,161} \right)\) |
\(\left[ {161;\,\,164} \right)\) |
\(\left[ {164;\,\,167} \right)\) |
|
Số học sinh |
5 |
12 |
15 |
8 |
Tỉ lệ học sinh có chiều cao từ 158 cm đến dưới 161 cm là
A. \(12,5\% \).
B. \(30\% \).
C. \(37,5\% \).
D. \(20\% \).
Mẫu số liệu ghép nhóm về lượng rau (đơn vị: tấn) thu được trong một năm của các đội sản xuất ở một hợp tác xã như bảng sau:
|
Lượng rau (tấn) |
\(\left[ {5;\,\,10} \right)\) |
\(\left[ {10;\,\,15} \right)\) |
\(\left[ {15;\,\,20} \right)\) |
\(\left[ {20;\,\,25} \right)\) |
\(\left[ {25;\,\,30} \right)\) |
\(\left[ {30;\,\,35} \right)\) |
Cộng |
|
Tần số |
2 |
4 |
3 |
5 |
4 |
2 |
\(N = 20\) |
Mẫu số liệu được chia thành số nhóm là
A. 4.
B. 5.
C. 6.
D. 7.
Bạn Ninh gieo một con xúc xắc liên tiếp hai lần. Số phần tử của không gian mẫu là
A. 6.
B. 12.
C. 36.
D. 24.
Một hộp chứa một quả bóng xanh, một quả bóng đỏ, một quả bóng vàng (các quả bóng có cùng khối lượng, kích thước). Lan lấy ra ngẫu nhiên hai quả bóng từ hộp. Xác suất của biến cố “Trong hai quả bóng lấy ra có quả bóng màu vàng” là
A. \(\frac{1}{3}\).
B. \(\frac{5}{6}\).
C. \(\frac{1}{6}\).
D. \(\frac{2}{3}\).
Biểu đồ tần số ở hình dưới đây biểu diễn số lượng laptop bán được của một cửa hàng trong bốn tháng 4, 5, 6, 7.
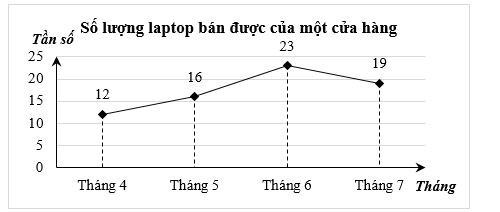
Nếu mỗi laptop bán ra cửa hàng được lãi 800 000 đồng thì sau bốn tháng 4, 5, 6, 7 cửa hàng thu được số tiền lãi là
A. 56 000 000 đồng.
B. 40 800 000 đồng.
C. 46 400 000 đồng.
D. 18 400 000 đồng.
Cho phép thử \(T,\) xét biến cố \(E.\) Kết quả của phép thử \(T\) làm cho biến cố \(E\) xảy ra được gọi là
A. Kết quả đúng với \(E.\)
B. Kết quả phù hợp với \(E.\)
C. Kết quả của \(E.\)
D. Kết quả thuận lợi cho \(E.\)
Phần thưởng trong một chương trình khuyến mãi của một cửa hàng là: ti vi, bàn ghế, tủ lạnh, máy tính, bếp từ, bộ bát đĩa. Bác Hoa tham gia chương trình được chọn ngẫu nhiên một mặt hàng. Gọi \(A\) là biến cố: “Bác Hoa chọn được mặt hàng là đồ điện”. Xác suất của biến cố \(A\) là
A. \(\frac{1}{2}\).
B. \(\frac{1}{6}\).
C. \(\frac{2}{3}\).
D. \(\frac{1}{3}\).
Độ dài các cạnh của tam giác \(ABC\) là \(BC = 5,\,\,AB = 3,\,\,AC = 4.\) Số đo của góc \(ABC\) (làm tròn đến phút) bằng
A. \(53^\circ 7'.\)
B. \(53^\circ \).
C. \(53^\circ 13\prime \).
D. \(53^\circ 8\prime \).
Hai con thuyền \(P\) và \(Q\) cách nhau 300 m và thẳng hàng với chân \(B\) của tháp hải đăng ở trên bờ biển. Từ \(P\) và \(Q\) người ta nhìn thấy tháp hải đăng dưới các góc \(\widehat {BPA} = 14^\circ \) và \(\widehat {BQA} = 42^\circ .\) Đặt \(h = AB\) là chiều cao của tháp hải đăng.
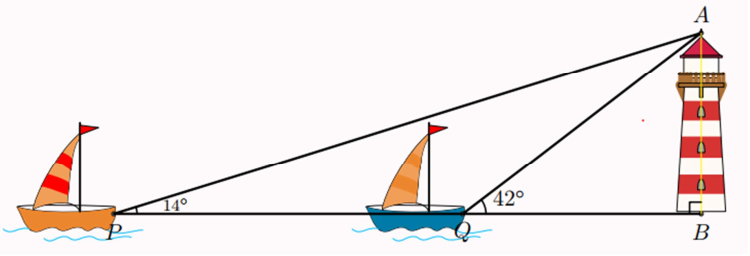
Khi đó chiều cao của tháp hải đăng (làm tròn đến hàng đơn vị) là
A. \[103,4\] m.
B. \[103,5\] m.
C. 103 m.
D. 104 m.
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\). Biết \(AC = 16\;{\rm{cm}}\) và \(\widehat {B\,} = 60^\circ .\) Độ dài đường cao \(AH\) là
A. \(AH = 8\;{\rm{cm}}\).
B. \(AH = 8\sqrt 3 \;{\rm{cm}}\).
C. \(AH = \frac{{16\sqrt 3 }}{3}\;{\rm{cm}}\).
D. \(AH = 16\sqrt 3 \;{\rm{cm}}\).
Cho tam giác \(ABC\) vuông tại \(A\). Khẳng định nào sau đây đúng?
A. \(\cos B = \frac{{AB}}{{BC}}\).
B. \(\cos B = \frac{{AC}}{{AB}}\).
C. \(\cos B = \frac{{AB}}{{AC}}\).
D. \(\cos B = \frac{{AC}}{{BC}}\).
Hình nón có chiều cao bằng 12 cm, bán kính đáy bằng 9 cm thì diện tích xung quanh là
A. \(60\;{\rm{c}}{{\rm{m}}^2}\).
B. \(80\pi \;{\rm{c}}{{\rm{m}}^2}\).
C. \(135\pi \;{\rm{c}}{{\rm{m}}^2}\).
D. \(180\pi \;{\rm{c}}{{\rm{m}}^2}\).
Một cái trục lăn sơn có dạng một hình trụ. Đường kính của đường tròn đáy là 6 cm, chiều dài lăn là 25 cm (hình bên). Sau khi lăn trọn 10 vòng thì trục lăn tạo nên mặt phẳng có diện tích là

A. \(1500\pi \;{\rm{c}}{{\rm{m}}^2}\).
B. \(150\pi \;{\rm{c}}{{\rm{m}}^2}\).
C. \(300\pi \;{\rm{c}}{{\rm{m}}^2}\).
D. \(3000\pi \;{\rm{c}}{{\rm{m}}^2}\).
Cho đường tròn \(\left( {O;\,\,R} \right).\) Hai tiếp tuyến của đường tròn cắt nhau tại \(M.\) Biết \(OM = R\sqrt 2 ,\) số đo góc tạo bởi hai tiếp tuyến bằng
A. \(45^\circ \).
B. \(60^\circ \).
C. \(30^\circ \).
D. \(90^\circ \).
Cho tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(AC.\) Biết \(\widehat {DBC} = 55^\circ \) (hình vẽ bên). Số đo \(\widehat {ACD}\) bằng

A. \(30^\circ \).
B. \(40^\circ \).
C. \(35^\circ \).
D. \(45^\circ \).
Cho đường tròn \(\left( O \right),\) từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA,\,\,MB\)\((A,\,\,B\) là tiếp điểm) sao cho \(\widehat {AOM} = 60^\circ .\) Góc ở tâm do hai tia \(OA,\,\,OB\) tạo ra có số đo bằng
A. \(30^\circ \).
B. \(60^\circ \).
C. \(120^\circ \).
D. \(180^\circ \).
Bán kính đường tròn ngoại tiếp tam giác đều cạnh 6 cm là
A. \(2\sqrt 3 \;{\rm{c}}{{\rm{m}}^2}\).
B. \(\sqrt 3 \;{\rm{cm}}\).
C. \(3\sqrt 3 \;{\rm{cm}}\).
D. \(2\sqrt 3 \;{\rm{cm}}\).
Cho đường tròn \(\left( {O;\,\,3\;{\rm{cm}}} \right)\) và điểm \(M\) nằm ngoài \(\left( O \right)\) sao cho \(OM = 5\;{\rm{cm}}{\rm{.}}\) Từ \(M\) kẻ đường thẳng \(d\) không đi qua tâm \(O\) cắt \(\left( O \right)\) tại hai điểm \(A,\,\,B.\) Tính tích \(MA \cdot MB\) ta được kết quả là
A. \(MA \cdot MB = 15\).
B. \(MA \cdot MB = 16\).
C. \(MA \cdot MB = 10\).
D. \(MA \cdot MB = 30\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 6\;{\rm{cm}};\,\,AC = 8\;{\rm{cm}}{\rm{.}}\) Bán kính đường tròn ngoại tiếp tam giác \(ABC\) là
A. 5.
B. 10.
C. 4.
D. 3.

