50 CÂU HỎI
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:
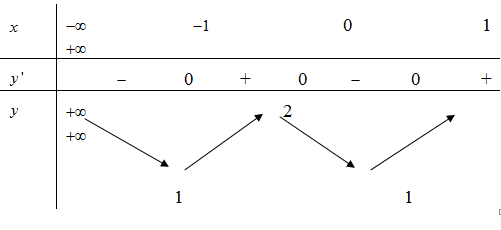
Số nghiệm thực của phương trình là:
A. 4
B. 1
C. 3
D. 2
Cho hàm số y = f(x) có đồ thị như hình vẽ sau:
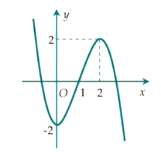
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A.
B. (0; 2)
C.
D. (-2; 2)
Thể tích của khối trụ có bán kính đáy r, chiều cao h bằng:
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên đoạn [-3; 3] bằng:
A. 20
B. 0
C. 4
D. -3
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng
A. M(1; 2; 5)
B. N(1; -2; 5)
C. Q(-1; 2; -5)
D. P(2; 3; 4)
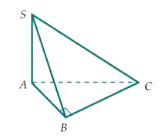
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
A.
B.
C.
D.
Cho hàm số f(x) liên tục trên bảng xét dấu f'(x) như sau:
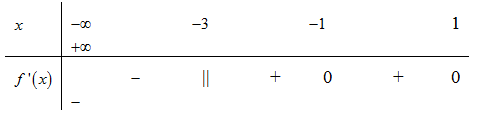
Số điểm cực trị của hàm số đã cho là:
A. 1.
B. 0
C. 2
D. 3
Thể tích của khối nón tròn xoay có đường kính đáy bằng 6 và chiều cao bằng 5 là:
A.
B.
C.
D.
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
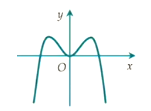
A.
B.
C.
D.
Trong không gian Oxyz, cho mặt cầu Tâm của (S) có tọa độ là:
A. (-1; 2; 3)
B. (1; -2; -3)
C. (-1; -2; -3)
D. (1; 2; 3)
Cho cấp số cộng có và Giá trị công sai d của cấp số cộng đó là:
A.
B. d = 3
C.
D. d = -3
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Cho hàm số f(x) có hàm số f'(x) liên tục trên [2; 3]. Khi đó bằng:
A. 3.
B. 10
C. -3
D. 7
Bất phương trình có tập nghiệm là:
A.
B.
C.
D. S = (-2; 0)
Họ tất cả các nguyên hàm của hàm số f(x) = cos 2x là:
A.
B.
C.
D.
Họ tất cả các nguyên hàm của hàm số trên khoảng là:
A.
B.
C.
D.
Diện tích của mặt cầu bán kính R bằng:
A.
B.
C.
D.
Trong không gian Oxyz, cho mặt phẳng Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.
B.
C.
D.
Trên giá sách có 8 quyển sách Văn và 10 quyển sách Toán, các quyển này đôi một phân biệt. Hỏi có bao nhiêu cách chọn ra 1 quyển sách trên giá?
A. 80
B. 10
C. 8
D. 18
Trong không gian Oxyz, tọa độ của vectơ là:
A.
B.
C.
D.
Nghiệm của phương trình là:
A.
B. x = 2
C. x = 3
D.
Cho hàm số có bảng biến thiên như sau:
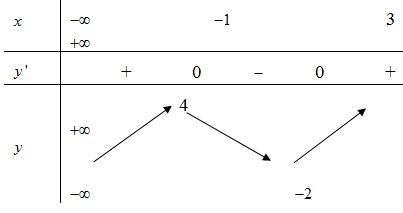
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
A. x = 3
B. x = -2
C. x = 4
D. x = -1
Ông A gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất 7% một năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi được nhập vào vốn ban đầu. Sau thời gian 10 năm nếu không rút lãi lần nào thì số tiền mà ông A nhận được gồm cả gốc lẫn lãi tính theo công thức nào dưới đây?
A. (đồng)
B. (đồng)
C. (đồng)
D. (đồng)
Môđun của số phức 2 + i là:
A.
B.
C. 3
D. 5
Với a là số thức dương tùy ý, bằng:
A.
B.
C.
D.
Gọi S là diện tích miền hình phẳng được gạch chéo trong hình vẽ dưới đây, với f(x) là hàm số liên tục trên
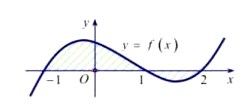
Công thức tính S là:
A.
B.
C.
D.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
A. 1
B. 0
C. 3
D. 2
Cho hàm số có đồ thị như hình vẽ bên.
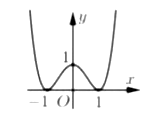
Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Trong không gian Oxyz, cho điểm M(2; -3; 1) và mặt phẳng Đường thẳng d đi qua điểm M và vuông góc với mặt phẳng có phương trình là:
A.
B.
C.
D.
Trên mặt phẳng tọa độ, điểm biểu diễn số phức là điểm nào dưới đây?
A. P(3; 4)
B. M(5; 4)
C. N(4; 5)
D. Q(4; 3)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên SA vuông góc với đáy, góc Tính thể tích khối chóp đã cho bằng:
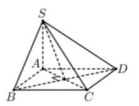
A.
B.
C.
D.
Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tích là một số lẻ bằng:
A.
B.
C.
D.
Cho hai số phức và Phần ảo của số phức bằng:
A. 0
B. -2
C. -4
D. 4
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm I(-1; 2; 1) và đi qua điểm A(0; 4; -1) là:
A.
B.
C.
D.
Trong không gian Oxyz, cho Vectơ có độ dài bằng:
A. 2
B.
C. 1
D. 3
Cho phương trình (m là tham số thực). Tập hợp tất cả các giá trị m để phương trình đã cho có hai nghiệm phân biệt thuộc [9; 27] là:
A. [4; 5]
B. (4; 5]
C. [2; 3]
D. [2; 3)
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng
A. 1
B. 3
C. 5
D. 2
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn
[1; 3] bằng 18. Tổng tất cả các phần tử của S bằng:
A. -2
B. 9
C. 7
D. 0
Trong không gian Oxyz, cho hai điểm A(4; 1; 0) và B(2; -1; 2). Phương trình mặt phẳng đường trung trực đoạn thẳng AB là:
A.
B.
C.
D.
Cho các số thực dương a, b khác 1 thỏa mãn và ab = 64. Giá trị của biểu thức bằng:
A.
B. 20
C. 25
D. 32
Cho hình trụ có chiều cao bằng Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh của hình trụ đã cho bằng:
A.
B.
C.
D.
Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông cạnh a, SO vuông góc với mặt phẳng (ABCD) và SO = a. Khoảng cách giữa SC và AB bằng:
A.
B.
C.
D.
Cho hàm số y = f(x) có bảng biến thiên như sau:
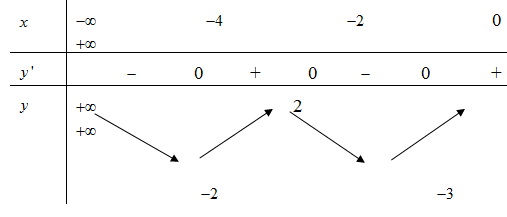
Số giá trị nguyên của tham số m để phương trình có ít nhất 5 nghiệm thực phân biệt thuộc khoảng là:
A. 12
B. 14
C. 11
D. 13
Cho hai số phức là hai nghiệm của phương trình biết Giá trị của biểu thức bằng:
A.
B.
C.
D.
Cho hàm số f(x) liên tục trên và có một nguyên hàm là hàm số Khi đó bằng:
A.
B.
C.
D.
Trong không gian Oxyz, cho ba điểm Gọi (P) là mặt phẳng chứa BC và cách A một khoảng lớn nhất. Hỏi vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?
A.
B.
C.
D.
Cho hàm số f(x) có đạo hàm liên tục trên thỏa mãn f(0) = 3 và Tích phân bằng:
A.
B.
C.
D.
Cho hình vuông ABCD có các đỉnh A, B, C tương ứng nằm trên đồ thị của các hàm số và Biết rằng diện tích hình vuông bằng 36, cạnh AB song song với trục hoành. Khi đó a bằng:
A.
B.
C.
D.
Cho khối chóp S.ABC có đáy là tam giác vuông tại Biết rằng góc giữa đường thẳng SB và mặt phẳng đáy bằng thể tích khối chop đã cho bằng:
A.
B.
C.
D.
Có bao nhiêu số nguyên a thuộc đoạn [-20; 20] sao cho hàm số có cực đại?
A. 18
B. 17
C. 36
D. 35


